题目
设二阶可导函数 $f(x)$ 满足 $f(1) = f(-1) = 1$, $f(0)=-1$, 且 $f^{”}(x)>0$, 则 $?$
$$A. \int_{-1}^{1} f(x) dx > 0$$
$$B. \int_{-1}^{1} f(x) dx < 0$$
$$C. \int_{-1}^{0} f(x) dx > \int_{0}^{1} f(x) dx$$
$$D. \int_{-1}^{0} f(x) dx < \int_{0}^{1} f(x) dx$$
解析
方法一：
由 $f^{”}(x)>0$ 可推知：
$$
f(x) = x^{2}.
$$
又由 $f(0)=-1$ 可推知：
$$
f(x) = x^{2} – 1.
$$
又由 $f(1) = f(-1) = 1$ 可推知：
$$
f(x) = 2 x^{2} – 1.
$$
于是，由于 $f(x)$ 关于 $y$ 轴对称，所以 $C,D$ 选项错误。
又：
$$
\int_{-1}^{1} f(x) dx =
$$
$$
\int_{-1}^{1} (2 x^{2} – 1) dx =
$$
$$
\int_{-1}^{1} (2 x^{2}) dx – \int_{-1}^{1} 1 dx =
$$
$$
2 \cdot \frac{1}{3} x^{3} |{-1}^{1} – x |{-1}^{1} =
$$
$$
[\frac{2}{3} + \frac{2}{3}] – [1+1] =
$$
$$
\frac{4}{3} – \frac{6}{3} = – \frac{2}{3} < 0.
$$
于是，$B$ 选项正确。
方法二：
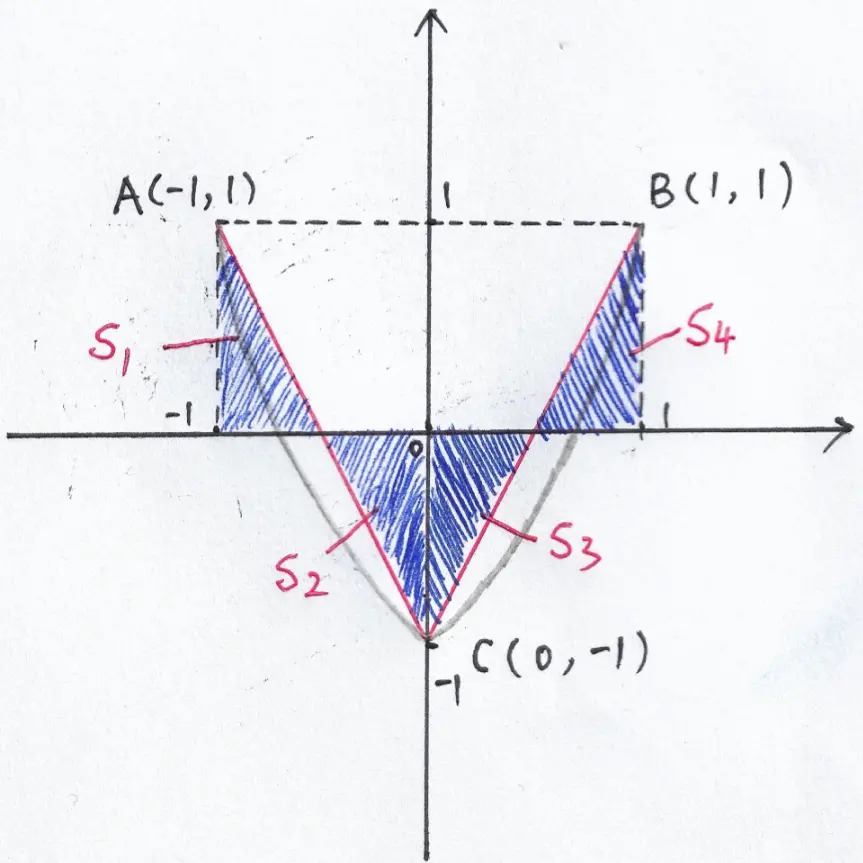
如图 1 所示，用红色折线将 $A,B,C$ 三个点连接起来，此时会形成 $s_{1}, s_{2}, s_{3}, s_{4}$ 四个小三角形，且：
$$
s_{1} = s_{2} = s_{3} = s_{4}.
$$
则可知，红色折线在区间 $[-1,1]$ 上与坐标轴围成的的面积的代数和为 $0$.
又由 $f^{”}(x)>0$ 可知，$f(x)$ 的曲线是凹的，$f(x)$ 的大致图像如图 1 中灰色线条所示，因此，$f(x)$ 在区间 $[-1,1]$ 上与坐标轴围成的面积的代数和一定小于 $0$, 即选项 $B$ 正确。
综上可知，正确选项为 $B$.
EOF