一、题目
函数 $f(x)$ $=$ $|x \sin x| \mathrm{e}^{\cos x}$, $x \in(-\infty, +\infty)$, 是 ( )
A. 单调函数
C. 有界函数
B. 周期函数
D. 偶函数
难度评级:
二、解析 
根据《单路径约束法判断函数的周期性》这篇笔记,我们可以绘制如图 01 所示的三条路径:
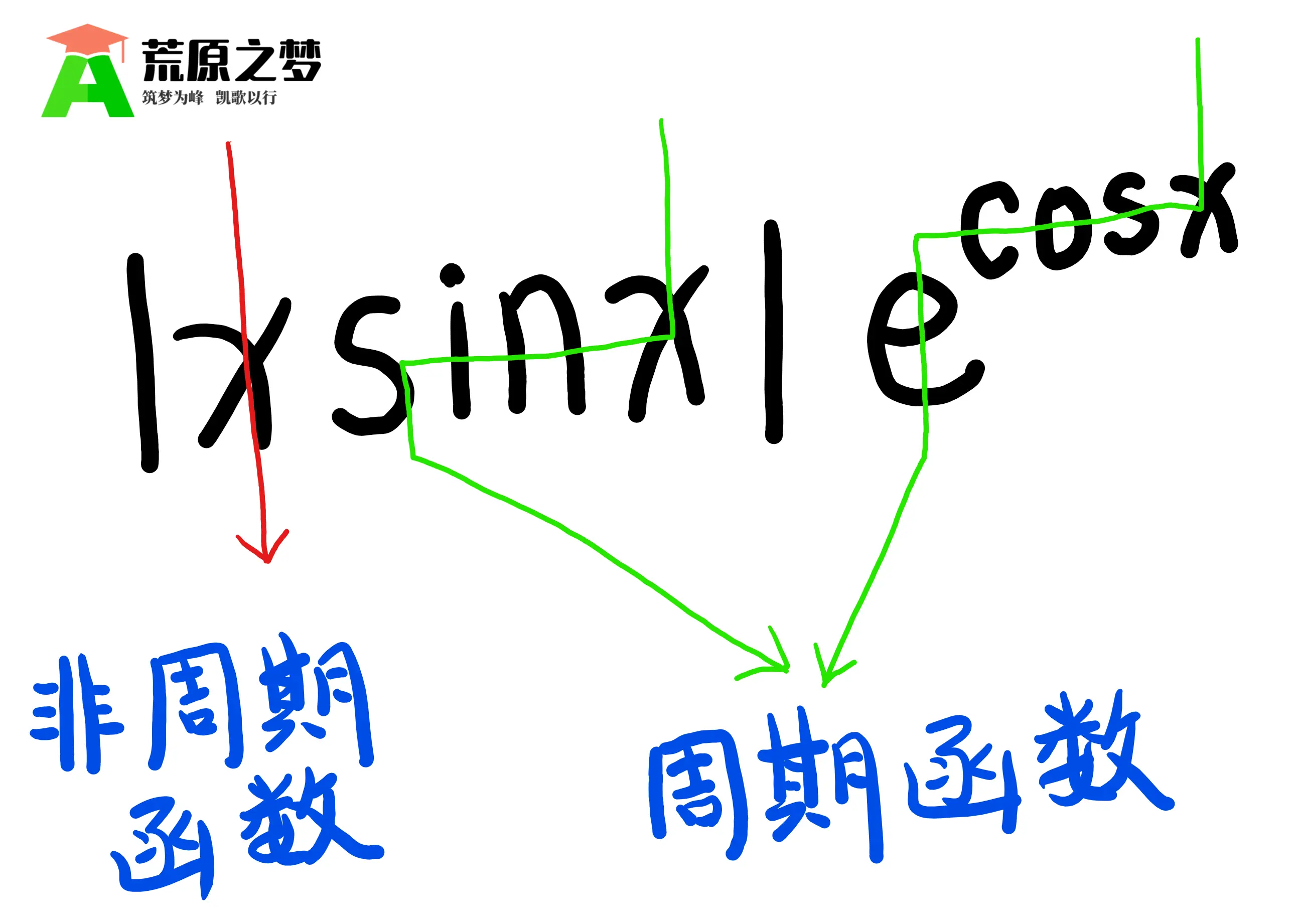
由上图可以看出,该函数存在一条红色的非周期性“路径”和两条绿色的周期性“路径”,因此,我们可以直接判断出,函数 $f(x)$ 不是一个周期函数。
同时由于非周期性的红色“路径”不是一个单调函数,因此,函数 $f(x)$ 也不是一个单调也不是有界函数。
综上,可以直接排除 A、B 和 C 三个选项,只有 D 选项正确。
当然,我们也可以通过一些计算排除 A、B 和 C 三个选项。
根据绝对值的运算规律,我们有:
$$
\begin{aligned}
f(x) \\
& = |x \sin x| \mathrm{e}^{\cos x} \\
& = \textcolor{orangered}{|x|} \cdot \textcolor{springgreen}{|\sin x|} \mathrm{e}^{\cos x}
\end{aligned}
$$
由于 $|x|$ 是一个单调增或减,$|\sin x|$ 不恒等于 $0$ 且 $\mathrm{e}^{\cos x}>0$, 因此可以判断出 $f(x)$ 既不是有界函数, 也不是周期函数。
接着,由于:
$$
\begin{cases}
f(0)=0 \\
f\left(\frac{\pi}{2}\right) = \frac{\pi}{2} \\
f(\pi)=0
\end{cases}
$$
于是可知,函数 $f(x)$ 不是单调函数。
又由于在区间 $(-\infty,+\infty)$ 中,有:
$$
\begin{aligned}
f(\textcolor{springgreen}{-x}) \\
& = |(-x) \sin (-x)| \mathrm{e}^{\cos (-x)} \\
& = |x \sin x| \mathrm{e}^{\cos x} \\
& = f(\textcolor{springgreen}{x})
\end{aligned}
$$
因此,函数 $f(x)$ 是偶函数,选项 D 正确。
高等数学
涵盖高等数学基础概念、解题技巧等内容,图文并茂,计算过程清晰严谨。
线性代数
以独特的视角解析线性代数,让繁复的知识变得直观明了。
特别专题
通过专题的形式对数学知识结构做必要的补充,使所学知识更加连贯坚实。