旋转体知识点综合题：弧长、体积、侧面积

一、题目

已知，星形线方程为：

$$
\left\{\begin{array}{l}
x=a \cos ^{3} t \\
y=a \sin ^{3} t
\end{array}\right.
$$

则它所围成的面积 $A=?$, 它的弧长 $L=?$, 它绕 $X$ 轴旋转而生成的旋转体体积 $V=?$, 该旋转体的侧面积 $S=?$

难度评级：

二、解析

根据题目，我们可以绘制出如图所示的示意图：

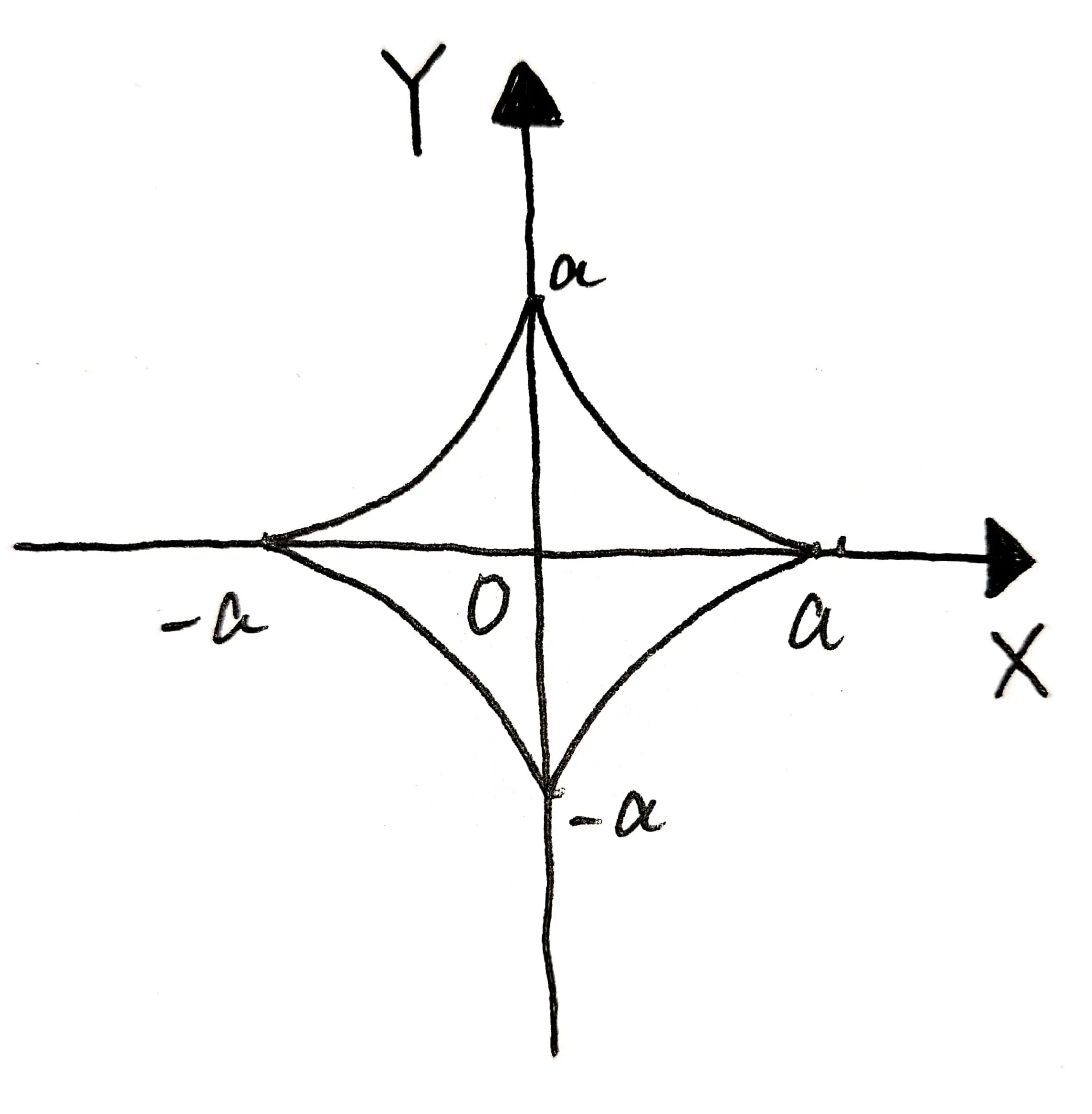
解答本题的需要注意两方面的内容：

1. $x$ 的取值范围与 $t$ 的取值范围之间的对应关系：$x = 0$ 时，$\cos t = 0$, 于是 $t = \frac{\pi}{2}$, 同理，$x = a$ 时，$\cos t = 1$, 于是 $t = 0$. 因此，当 $x \in (0, a)$ 时，$t \in (\frac{\pi}{2}, 0)$;

2. 去根号的时候一定要看是否需要加绝对值。

面积 A

$$
A=4 \int_{0}^{a} y \mathrm{~ d} x \Rightarrow
$$

$$
A=4 \int_{\frac{\pi}{2}}^{0}\left(a \sin ^{3} t\right) \mathrm{~ d} \left(a \cos ^{3} t\right)=
$$

$$
4 \int_{\frac{\pi}{2}}^{0}\left(a \sin ^{3} t\right)\left[3 a \cos ^{2} t(-\sin t)\right] \mathrm{~ d} t=
$$

$$
4 \int_{0}^{\frac{\pi}{2}} 3 a^{2} \sin ^{4} t \cos ^{2} t \mathrm{~ d} t=.
$$

$$
12 a^{2} \int_{0}^{\frac{\pi}{2}} \sin ^{4} t\left(1-\sin ^{2} t\right) \mathrm{~ d} t=
$$

$$
12 a^{2} \int_{0}^{\frac{\pi}{2}}\left(\sin ^{4} t-\sin ^{6} t\right) \mathrm{~ d} t=
$$

$$
12 a^{2}\left(\frac{3}{4} \cdot \frac{1}{2} \cdot \frac{\pi}{2}-\frac{5}{6} \cdot \frac{3}{4} \cdot \frac{1}{2} \cdot \frac{\pi}{2}\right)=
$$

$$
12 a^{2} \cdot \frac{1}{6} \cdot \frac{3}{4} \cdot \frac{1}{2} \cdot \frac{\pi}{2}=\frac{3 \pi a^{2}}{8}
$$

弧长 L

设第一象限内的弧长为 $L_{1}$, 则：

$$
L_{1}=\int_{0}^{\frac{\pi}{2}} \sqrt{x^{\prime 2}(t)+y^{2}(t)} \mathrm{~ d} t=
$$

$$
\int_{0}^{\frac{\pi}{2}} \sqrt{9 a^{2}\left(\cos ^{4} t \sin ^{2} t+\sin ^{4} t \cos ^{2} t)\right.} \mathrm{~ d} t=
$$

$$
3 a \int_{0}^{\frac{\pi}{2}} | \cos t \sin t \mid \mathrm{~ d} t=3 a \int_{0}^{\frac{\pi}{2}}\left(\cos t \sin t\right) \mathrm{~ d} t=
$$

$$
3 a \int_{0}^{\frac{\pi}{2}} \sin t \mathrm{~ d} (\sin t)=\left.3 a \cdot \frac{1}{2} \sin ^{2} t\right|_{0} ^{\frac{\pi}{2}}=\frac{3 a}{2}
$$

于是，总的弧长为：

$$
L=4 \times L_{1}=4 \times \frac{3 a}{2}=6 a
$$

旋转体的体积 V

$$
V=
$$

$$
2 \cdot \pi \int_{0}^{a} y^{2} \mathrm{~ d} x=2 \pi \int_{\frac{\pi}{2}}^{0} a^{2} \sin ^{6} t \mathrm{~ d} \left(a \cos ^{3} t\right)=
$$

$$
2 \pi \int_{\frac{\pi}{2}}^{0} a^{2} \sin ^{6} t\left[a \cdot 3 \cdot \cos ^{2} t(-\sin t)\right] \mathrm{~ d} t=
$$

$$
2 \pi \int_{0}^{\frac{\pi}{2}} 3 a^{3} \sin ^{7} t \cos ^{2} t \mathrm{~ d} t=
$$

$$
6 a^{3} \pi \int_{0}^{\frac{\pi}{2}} \sin ^{7} t\left(1-\sin ^{2} t\right) \mathrm{~ d} t=
$$

$$
6 a^{3} \pi\left[\frac{6}{7} \cdot \frac{4}{5} \cdot \frac{2}{3} \cdot 1-\frac{8}{9} \cdot \frac{6}{7} \cdot \frac{4}{5} \cdot \frac{2}{3} \cdot 1\right]=
$$

$$
6 a^{3} \pi \cdot \frac{1}{9} \cdot \frac{6}{7} \cdot \frac{4}{5} \cdot \frac{2}{3}=\frac{32 \pi a^{3}}{105}
$$

侧面积 S

根据《旋转体侧面积的计算公式》，有：

$$
S= 2 \pi \int_{0}^{\pi}|y| \sqrt{x^{2}(t)+y^{\prime 2}(t)} \mathrm{~ d} t=
$$

$$
S=2 \pi \int_{0}^{\pi} a \sin^{3} t \sqrt{9a^{2} (\cos ^{4} t \sin^{2} t + \sin^{4} t \cos ^{2} t)} \mathrm{~ d} t=
$$

去根号先加绝对值：

$$
S=6 a^{2} \pi \int_{0}^{\pi} \sin^{3} t \cdot \textcolor{springgreen}{ | \cos t \sin t | } \mathrm{~ d} t=
$$

$$
S=6 a^{2} \pi \int_{0}^{\pi} \sin^{4} t \cdot \textcolor{springgreen}{ | \cos t | } \mathrm{~ d} t=
$$

通过划分区间取绝对值：

$$
S=6 a^{2} \pi\left[\int_{0}^{\frac{\pi}{2}} \sin ^{4} t \mathrm{~ d} (\sin t)-\int_{\frac{\pi}{2}}^{\pi} \sin ^{4} t \mathrm{~ d} (\sin t)\right] =
$$

$$
S = 6a^{2} \pi\left[\left.\frac{1}{5} \sin ^{5} t\right|_{0} ^{\frac{\pi}{2}}-\left.\frac{1}{5} \sin ^{5} t\right|_{\frac{\pi}{2}} ^{\pi}\right] \Rightarrow
$$

$$
S = 6a^{2} \pi\left[\frac{1}{5}(1-0)-\frac{1}{5}(0-1)\right] \Rightarrow
$$

$$
S=6 a^{2} \pi \cdot \frac{2}{5}=\frac{12 \pi a^{2}}{5}
$$

---