旋转体的转轴不是 X 轴或者 Y 轴怎么办？先取反再平移

一、题目

摆线 $x=a(t-\sin t), y=a(1-\cos t)(0 \leqslant t \leqslant 2 \pi)$ 与 $x$ 轴围成图形绕 $y=2 a$ 旋转一周而得旋转体的体积 $V=?$

难度评级：

二、解析

根据题目信息，我们可以绘制出如下示意图（关于摆线的绘制，可以参考这篇文章）：

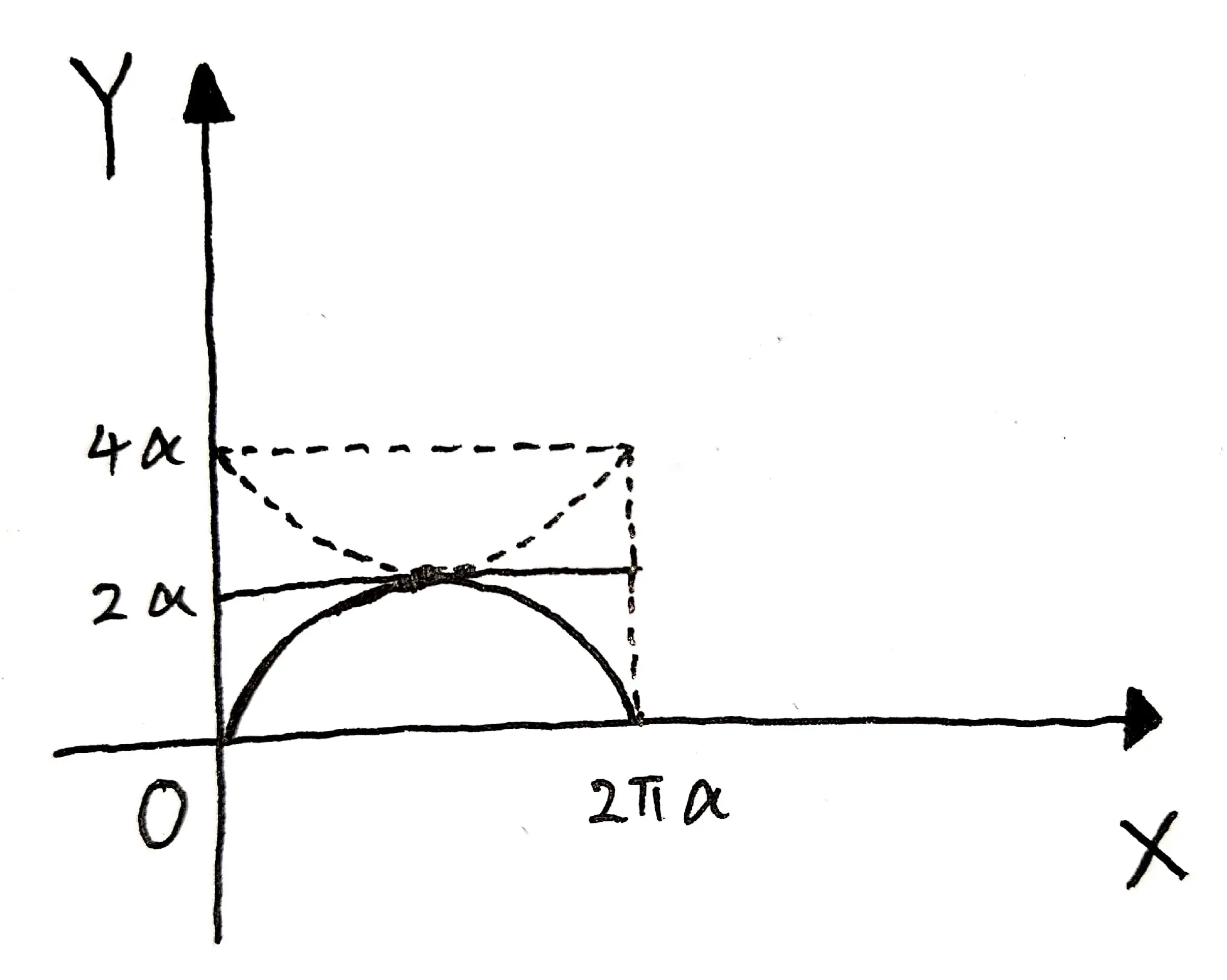
分析可知，用 $X$ 轴上长度为 $2 \pi a$ 的这段线旋转所形成的圆柱体的体积减去摆线绕 $y=2a$ 旋转所形成的体积 $V_{1}$ 就是我们要求解的旋转体的体积。

这里存在的一个问题就是，摆线既不是绕 $X$ 轴旋转，也不是绕 $Y$ 轴旋转，而是绕 $y = 2a$ 旋转。因此，我们需要做的首先是对摆线的方程 $y=a(1-\cos t)$ 取负，变成 $-y$, 这样就会映射到 $X$ 轴下方 $-2a$ 处，之后再加上 $2a$ 变成 $2a – y$ 就刚好成了绕 $X$ 轴旋转了。

$$
V_{1}=\pi \int_{0}^{2 \pi a}[2 a-y]^{2} \mathrm{~ d} x \Rightarrow
$$

把参数方程中 $x$ 和 $y$ 对应的表达式代入：

$$
V_{1}=\pi \int_{0}^{2 \pi}[2 a-a(1-\cos t)]^{2} d[a(t-\sin t)]
$$

$$
V_{1}=\pi \int_{0}^{2 \pi} a^{2}(1+\cos t)^{2}(a-a \cos t) \mathrm{~ d} t \Rightarrow
$$

$$
V_{1}=\pi \int_{0}^{2 \pi} a^{3}\left(1-\cos ^{2} t+\cos t-\cos ^{3} t\right) \mathrm{~ d} t \Rightarrow
$$

$$
V_{1}=a^{3} \pi \quad\left[\int_{0}^{2 \pi} 1 \mathrm{~ d} t-4 \int_{0}^{\frac{\pi}{2}} \cos ^{2} t \mathrm{~ d} t+0-0\right] \Rightarrow
$$

$$
V_{1}=a^{3} \pi\left[2 \pi-4 \cdot \frac{1}{2} \cdot \frac{\pi}{2}\right] \Rightarrow
$$

$$
V_{1}=a^{3} \pi^{2}
$$

于是：

$$
V=\pi(2 a)^{2} \cdot 2 \pi a-a^{3} \pi^{2}=7 a^{3} \pi^{2}
$$

---