求解函数 $f(x)$ $=$ $\ln x$ $-$ $\frac{x}{e}$ $+$ $k$ 零点的个数

一、题目

求解函数 $f(x)$ 的零点的个数：

$$f(x)=\ln x–\frac{x}{e}+k$$

其中，$k$ $>$ $0$.

难度评级：

二、解析

解题思路：函数 $f(x)$ 的零点就是函数 $f(x)$ 的图象与直角坐标系 $x$ 轴的交点——要找到这些“交点”，就要知道函数 $f(x)$ 的增减性，而要确定函数 $f(x)$ 的增减性，就要从函数 $f(x)$ 一阶导的正负性入手。

Next

首先：

$$f^{\prime }(x)=\frac{1}{x}–\frac{1}{e}.$$

Next

于是：

1. 当 $x$ $=$ $e$ 时，$f^{\prime }(x)$ $=$ $0$，$f(x)$ 取得极大值 $f(e)$ $=$ $k$, 其中 $k$ $>$ $0$;
2. 当 $0$ $<$ $x$ $<$ $e$ 时，$f^{\prime }(x)$ $>$ $0$, $f(x)$ 单调递增；
3. 当 $e$ $<$ $x$ 时，$f^{\prime }(x)$ $<$ $0$, $f(x)$ 单调递减；

注意：在分子一样的情况下，分母越大，整个分式的值越小。

Next

此外：

$$\underset{x\to 0}{lim}f(x)\Rightarrow$$

$$\underset{x\to 0}{lim}(\ln x–\frac{x}{e}+k)=–\mathrm{\infty }–0+k=–\mathrm{\infty }.$$

$$\underset{x\to \mathrm{\infty }}{lim}f(x)\Rightarrow$$

当 $x$ $\to$ $\mathrm{\infty }$ 时，$\ln x$ $\ll$ $\frac{1}{e}x$ $\Rightarrow$

$$\underset{x\to \mathrm{\infty }}{lim}(\ln x–\frac{x}{e}+k)=–\mathrm{\infty }.$$

Next

进而，我们可以画出关于函数 $f(x)$ 的如下图象示意图：

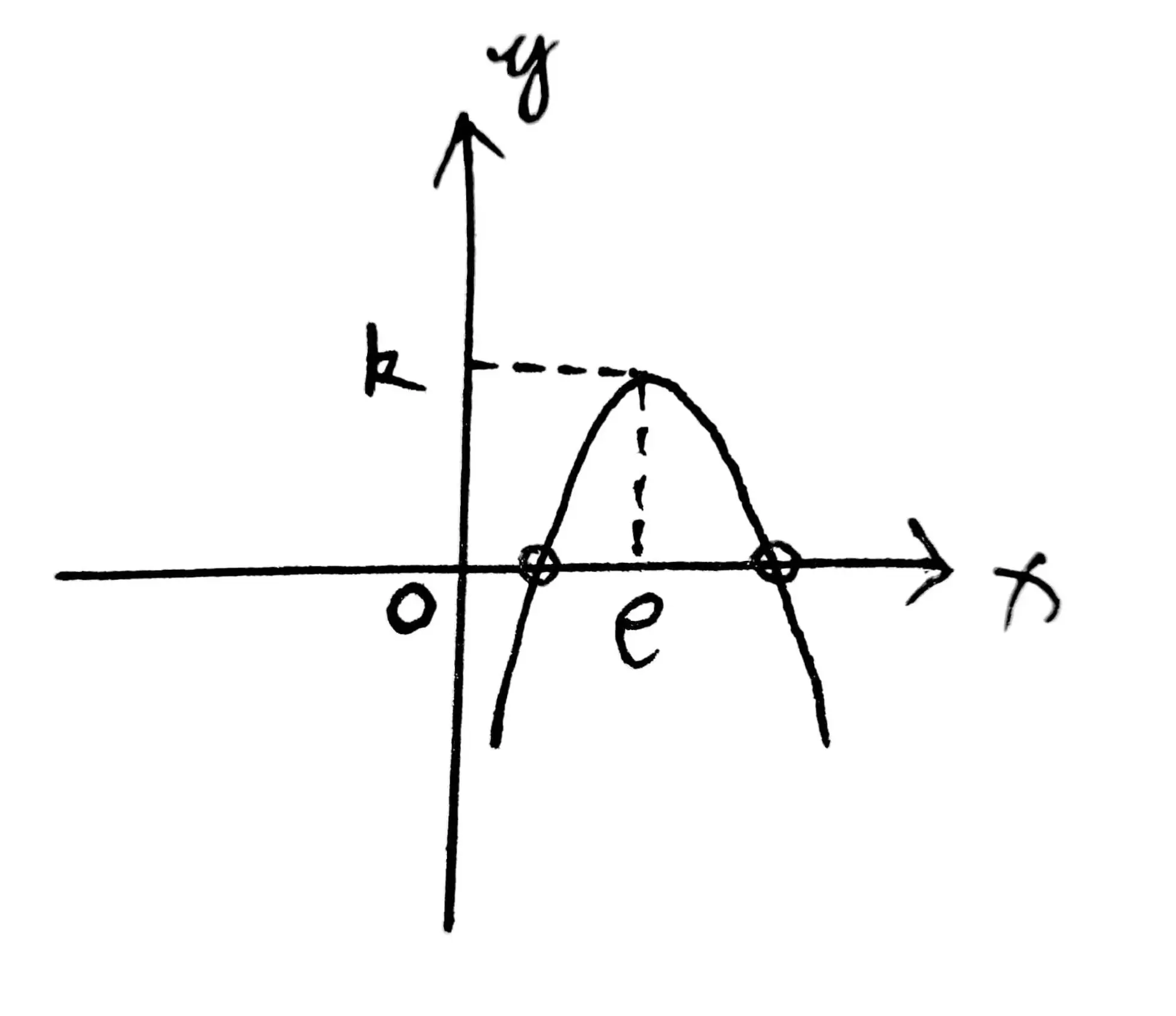
综上可知，函数 $f(x)$ 与 $x$ 轴有两个交点，因此，函数 $f(x)$ 存在两个零点。

---