题目
设平面区域 $D$ 由直线 $y=x$, 圆 $x^{2} + y^{2} = 2y$ 及 $y$ 轴所围成,则二重积分 $\iint xy d \sigma = ?$
解析
由题目中圆的方程 $x^{2} + y^{2} = 2y$ 可得:
$$
x^{2} + y^{2} = 2y \Rightarrow
$$
$$
x^{2} + y^{2} – 2y = 0 \Rightarrow
$$
$$
x^{2} + (y-1)^{2} = 1.
$$
于是可知,这是一个圆心坐标为 $(0,1)$, 半径 $r = 1$ 的圆。
根据题目中的信息,我们可以绘制出如下示意图(阴影部分为积分区域 $D$):
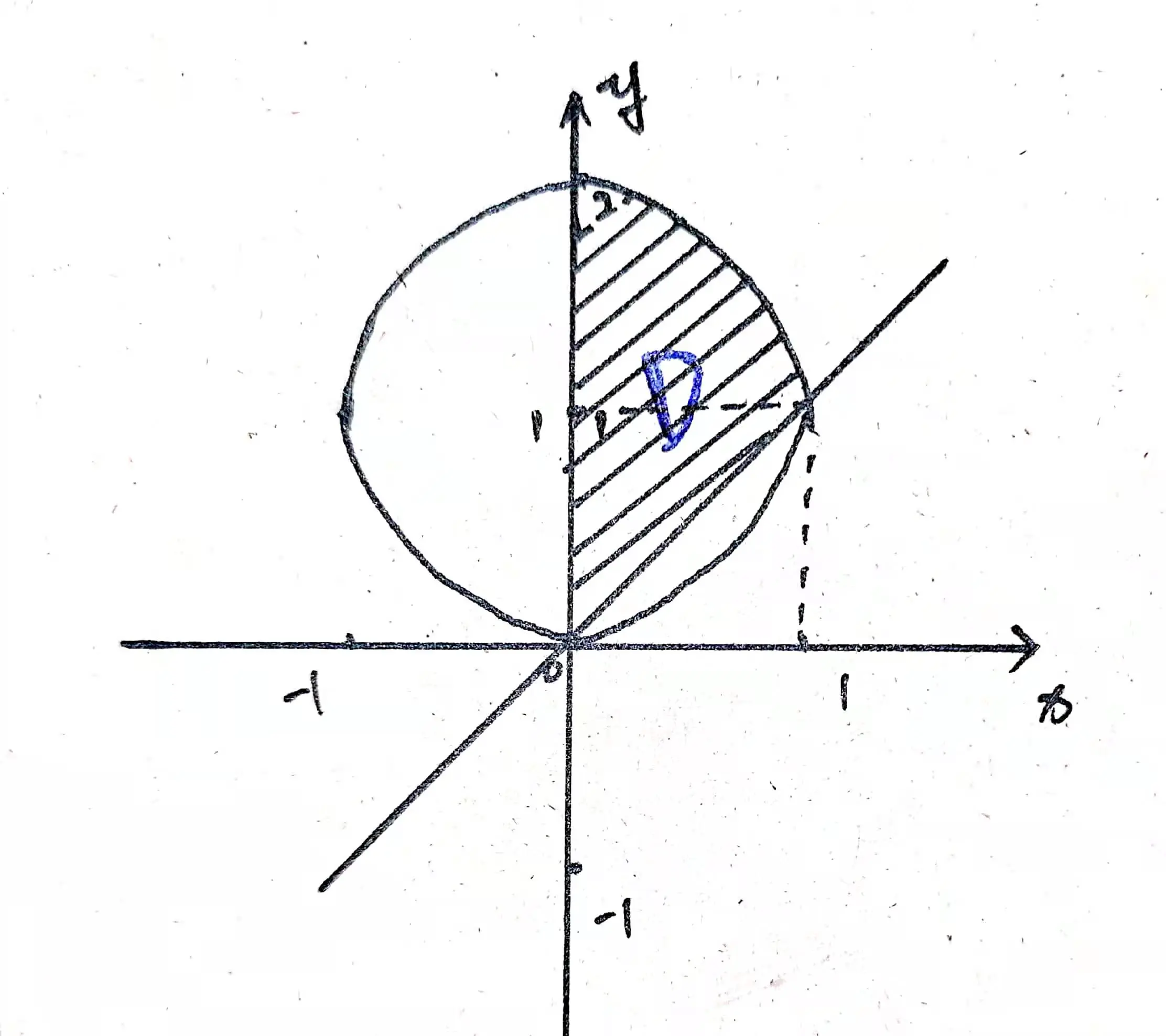
到这里可以知道,本题考查的就是二重积分的计算问题。具体到本题,我们有三种解法。
解法一
由于本题涉及到了圆形,在二重积分计算的问题中,只要涉及到了圆形,就可以考虑用极坐标系和极坐标方程来解。如下即为本题的极坐标解法。
已知,在极坐标系下:
$$
\left\{\begin{matrix}
x = r \cos \theta,\\
y = r \sin \theta.
\end{matrix}\right.
$$
又知,极坐标系下二重积分可表示为:
$$
\iint_{D} f(x, y) d x dy = \iint_{D} f(r \cos \theta, r \sin \theta) r dr d \theta
$$
于是:
$$
\iint_{D} xy d \sigma =
$$
$$
\iint_{D} r \cos \theta \cdot r \sin \theta \cdot r \cdot dr d \theta =
$$
$$
\iint_{D} r^{3} \cos \theta \sin \theta dr d \theta =
$$
$$
\int_{\frac{\pi}{4}}^{\frac{\pi}{2}} \cos \theta \sin \theta d \theta \int_{0}^{2 \sin \theta} r^{3} dr =
$$
$$
\int_{\frac{\pi}{4}}^{\frac{\pi}{2}} [(\cos \theta \sin \theta) \cdot (\frac{1}{4} r^{4} |_{0}^{2 \sin \theta})] d \theta =
$$
$$
4 \int_{\frac{\pi}{4}}^{\frac{\pi}{2}} \sin^{5} \theta \cos \theta d \theta =
$$
$$
4 \int_{\frac{\sqrt{2}}{2}}^{1} \sin^{5} \theta d (\sin \theta) =
$$
$$
4 \cdot \frac{1}{6} (\sin^{6} \theta) |_{\frac{\sqrt{2}}{2}}^{1} =
$$
$$
\frac{2}{3} \cdot (1 – (\frac{\sqrt{2}}{2})^{6}) =
$$
$$
\frac{2}{3} \cdot (1 – \frac{1}{8}) =
$$
$$
\frac{2}{3} \cdot \frac{7}{8} = \frac{7}{12}.
$$
注:上面式子中 $\int_{0}^{2 \sin \theta} r^{3} dr$ 中积分上限 $2 \sin \theta$ 的来历如图 02 所示,推导方式如下:
$$
\because \theta_{1} = 90^{\circ} – \theta_{3}
$$
$$
\theta_{2} = 180^{\circ} – 90^{\circ} – \theta_{3}
$$
$$
\therefore \theta_{1} = \theta_{2} = \theta
$$
$$
\because \sin \theta_{2} = \frac{r}{2}
$$
$$
\therefore r = 2 \sin \theta_{2} = 2 \sin \theta.
$$
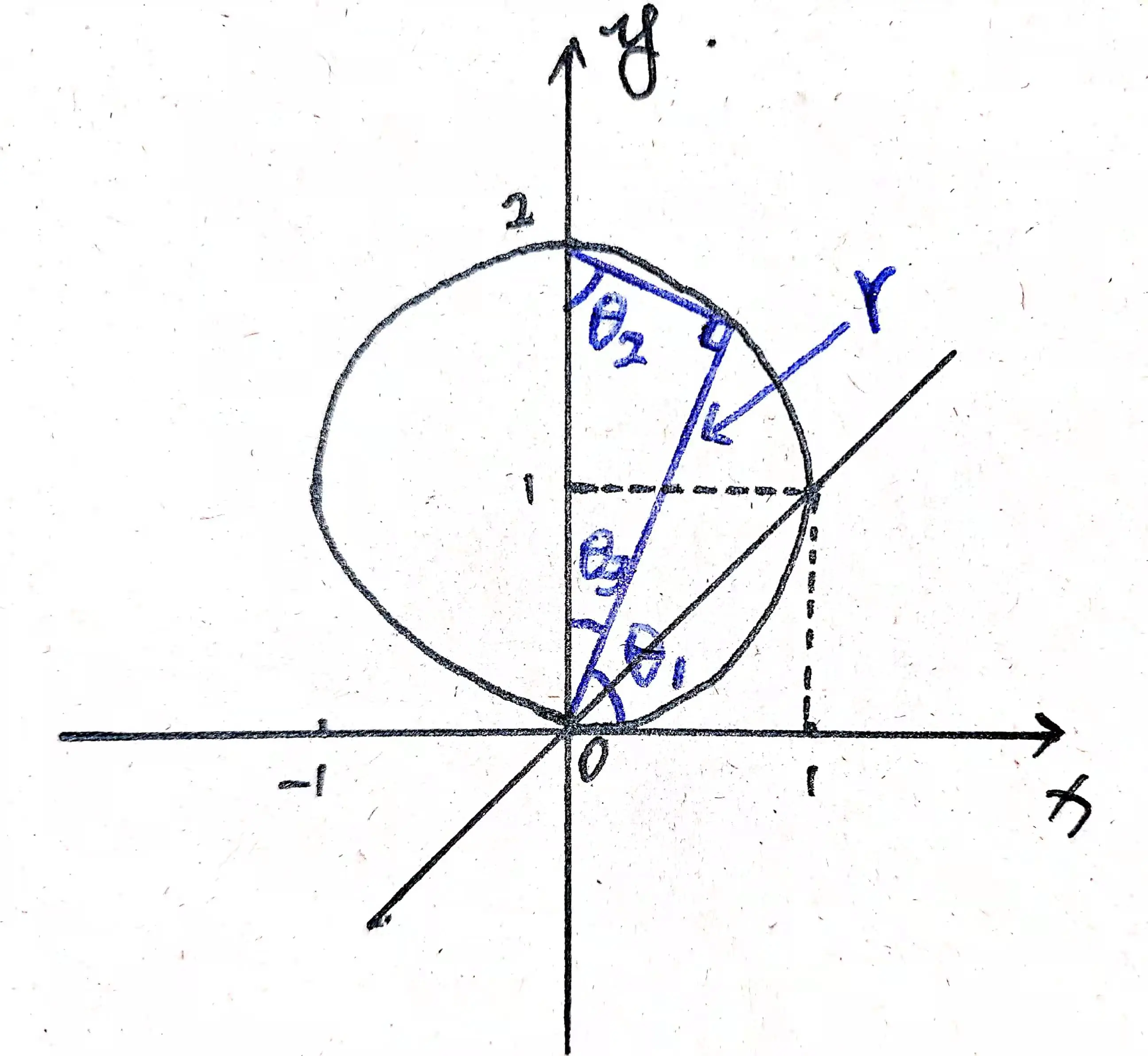
解法二
除了可以全部使用极坐标系计算之外,我们也可以将积分区域分割成 $D_{1}$, $D_{2}$ 两个区域(如图 03),分别用合适的方式求解。
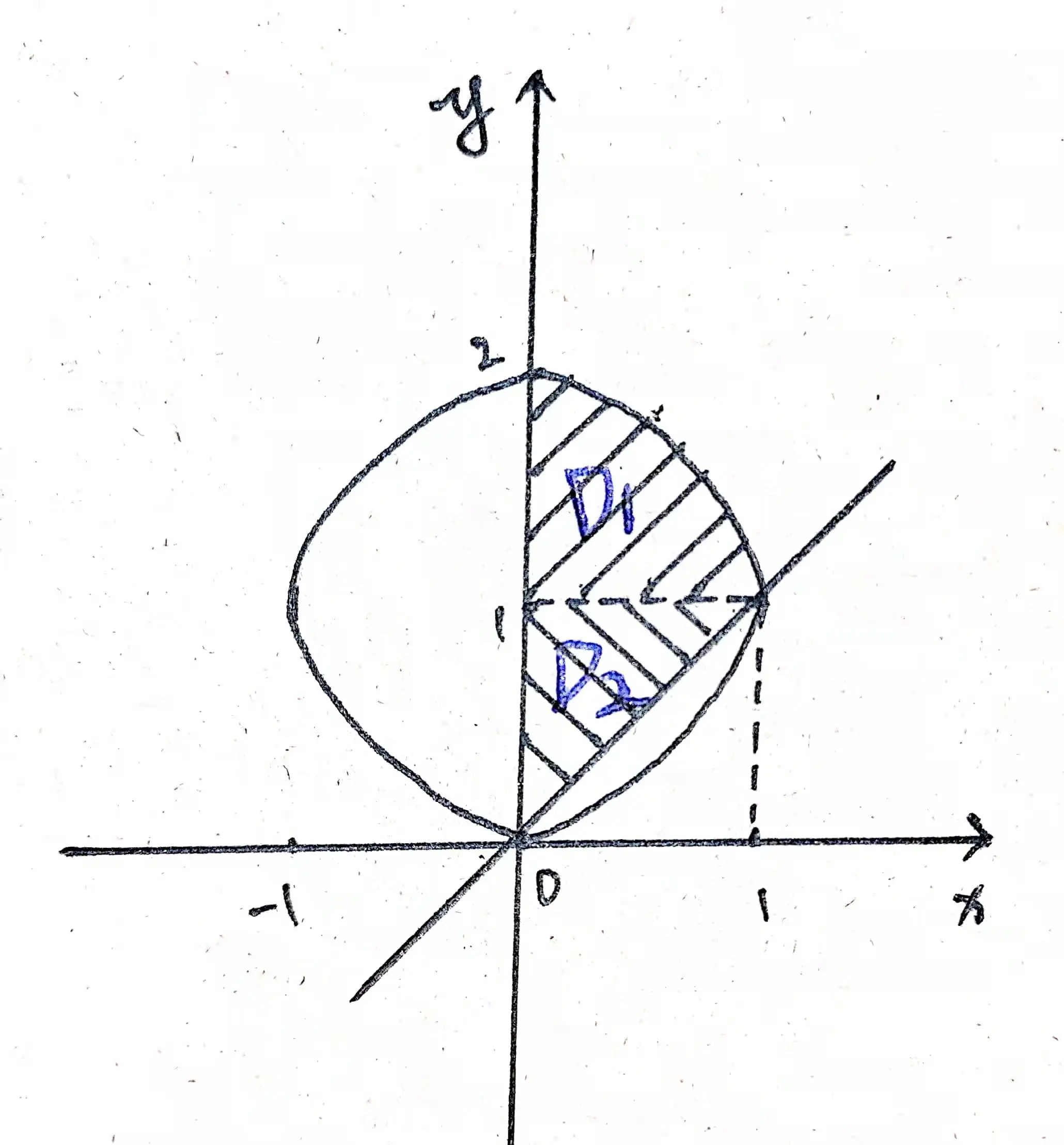
由题可知:
$$
\iint_{D} xy d \sigma = \iint_{D_{1}} xy d \sigma + \iint_{D_{2}} xy d \sigma.
$$
其中,对于 $D_{1}$ 区域,我们可令:
$$
\left\{\begin{matrix}
x = r \cos \theta,\\
y = r \sin \theta + 1.
\end{matrix}\right.
$$
于是:
$$
\iint_{D_{1}} xy d \sigma=
$$
$$
\iint_{D_{1}} (r \cos \theta) \cdot (r \sin \theta + 1) \cdot r dr d \theta =
$$
$$
\iint_{D_{1}} r(r^{2} \sin \theta \cos \theta + r \cos \theta) dr d \theta =
$$
$$
\iint_{D_{1}} (r^{3} \sin \theta \cos \theta + r^{2} \cos \theta) dr d\theta =
$$
$$
\int_{0}^{1} dr \int_{0}^{\frac{\pi}{2}} (r^{3} \sin \theta \cos \theta + r^{2} \cos \theta) d\theta =
$$
$$
\int_{0}^{1}[ r^{3}\int_{0}^{\frac{\pi}{2}} \sin \theta \cos \theta d \theta + r^{2} \int_{0}^{\frac{\pi}{2}} \cos \theta d \theta]dr =
$$
$$
\int_{0}^{1}[r^{3} \int_{0}^{1} \sin \theta d(\sin \theta) d\theta + r^{2} \cdot (1-0)]dr =
$$
$$
\int_{0}^{1} (\frac{1}{2} r^{3} + r^{2}) dr = \frac{1}{8} + \frac{1}{3}.
$$
对于 $D_{2}$ 区域,我们有:
$$
0 < y < 1;
$$
$$
0<x<y.
$$
于是:
$$
\iint_{D_{2}} xy d\sigma=
$$
$$
\int_{0}^{1} y dy \int_{0}^{y} x dx =
$$
$$
\int_{0}^{1}(y \cdot \frac{1}{2} y^{2}) dy =
$$
$$
\frac{1}{2} \int_{0}^{1} y^{3} dy =
$$
$$
\frac{1}{2} \cdot \frac{1}{4} = \frac{1}{8}.
$$
于是:
$$
D = D_{1} + D_{2} =
$$
$$
\frac{1}{3} + \frac{1}{8} + \frac{1}{8} = \frac{7}{12}.
$$
解法三
我们也可以完全不使用极坐标,在直角坐标系下也可以解决本题。
由题可知:
$$
x^{2} + y^{2} = 2y \Rightarrow
$$
$$
x^{2} + (y – 1)^{2} = 1 \Rightarrow
$$
$$
(y – 1)^{2} = 1-x^{2} \Rightarrow
$$
$$
y – 1 = \sqrt{1 – x^{2}} \Rightarrow
$$
$$
y = 1 + \sqrt{1-x^{2}}.
$$
于是,我们有:
$$
0<x<1;
$$
$$
x<y<1 + \sqrt{1-x^{2}}.
$$
即:
$$
\iint_{D} xy d \sigma =
$$
$$
\int_{0}^{1} x \cdot dx\int_{x}^{1+\sqrt{1-x^{2}}} y \cdot dy =
$$
$$
\int_{0}^{1} x \frac{1}{2}[(1+\sqrt{1-x^{2}})^{2} – x^{2}] dx =
$$
$$
\frac{1}{2} \int_{0}^{1} x(1+1-x^{2} + 2 \sqrt{1-x^{2}} – x^{2}) =
$$
$$
\frac{1}{2} \int_{0}^{1} (2x -2x^{3} +2x\sqrt{1-x^{2}}) dx =
$$
$$
\int_{0}^{1} (x – x^{3} + x \sqrt{1-x^{2}}) dx =
$$
$$
\int_{0}^{1} x dx – \int_{0}^{1} x^{3} dx + \int_{0}^{1} x \sqrt{1-x^{2}} dx \Rightarrow
$$
由于:
$$
[(1-x^{2})^{\frac{3}{2}}]^{‘} =
$$
$$
\frac{3}{2} (1-x^{2})^{\frac{1}{2}} (-2x) =
$$
$$
-3 x \sqrt{1-x^{2}}.
$$
于是:
$$
[-\frac{1}{3}(1-x^{2})^{\frac{3}{2}}]^{‘} = x \sqrt{1-x^{2}}.
$$
于是:
$$
\int_{0}^{1} x dx – \int_{0}^{1} x^{3} dx + \int_{0}^{1} x \sqrt{1-x^{2}} dx =
$$
$$
\frac{1}{2} – \frac{1}{4} -[\frac{1}{3}(1-x^{2})^{\frac{3}{2}}|_{0}^{1}] =
$$
$$
\frac{1}{2} – \frac{1}{4} – (0-\frac{1}{3}) =
$$
$$
\frac{1}{4} + \frac{1}{3} = \frac{7}{12}.
$$
注:在本题中,区间写成“大于 $>$”、“小于 $<$”或“大于等于 $\geqslant$”、“小于等于 $\leqslant$”都是一样的,不影响积分的结果。