题目
设 $I_{k} = \int_{0}^{k \pi} e^{x^{2}} \sin x dx$ $(k=1,2,3)$, 则有 $?$
$$
A. I_{1} < I_{2} < I_{3}
$$
$$
B. I_{3} < I_{2} < I_{1}
$$
$$
C. I_{2} < I_{3} < I_{1}
$$
$$
D. I_{2} < I_{1} < I_{3}
$$
解析
根据已知条件,我们可以画出函数 $y=e^{x^{2}}$ 的大致图像,如图 1 所示:
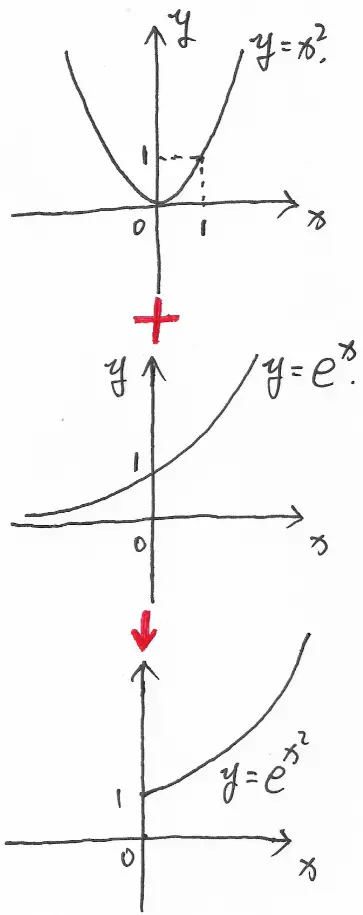
将 $y=e^{x^{2}}$ 和 $y=\sin x$ 画在一个坐标系内得到的大致图像如图 2 所示:
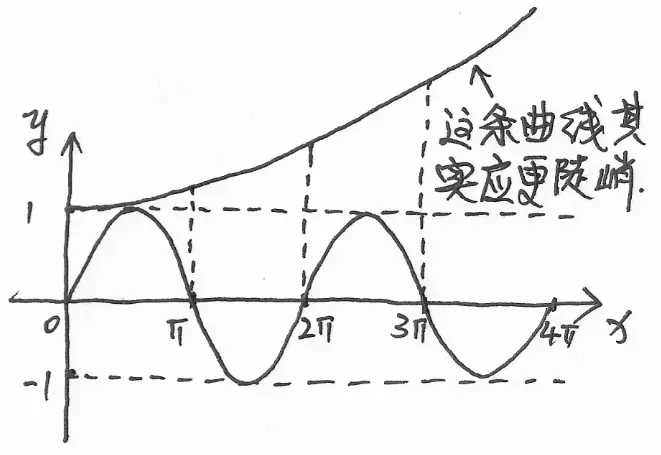
由图像可知,在 $[0, \pi]$ 区间内对 $y = e^{x^{2}} \sin x$ 进行积分时,由于 $y = e^{x^{2}}$ 和 $y = \sin x$ 的图像都是位于 $x$ 轴上方的,因此,$y=e^{x^{2}} \sin x$ 的积分值大于零,即 $I_{1}>0$.
在 $[\pi, 2 \pi]$ 区间内对 $y=e^{x^{2}} \sin x$ 进行积分时,由于 $y=e^{x^{2}}$ 的图像位于 $x$ 轴上方,$y=\sin x$ 的图像位于 $x$ 轴下方,且由于 $y=e^{x^{2}}$ 增长较快,因此 $y=e^{x^{2}} \sin x$ 在 $[\pi, 2\pi]$ 区间内的积分值是一个较大的负数,因此,$y=e^{x^{2}} \sin x$ 在 $[0, 2\pi]$ 上的积分值小于零,即 $I_{2}<0$.
同理可推测,由于 $y=e^{x^{2}}$ 增长较快,$y=e^{x^{2}} \sin x$ 在 $[2\pi, 3\pi]$ 上的积分值是一个较大的数,再加上 $y=e^{x^{2}} \sin x$ 在 $[0, \pi]$ 区间内的正数积分值能够抵消一部分 $y=e^{x^{2}} \sin x$ 在 $[\pi, 2\pi]$ 区间内的负数积分值,因此 $I_{3}>0$ 且 $I_{3}$ 【很可能】比 $I_{2}$ 大。
于是有:
$$
I_{2} < I_{1} < I_{3}.
$$
综上可知,正确选项为 $D$.
EOF