声明:本文所阐述的观点仅供参考,本文所得出的结论仅仅是思想实验的可能结果,没有经过实验验证。
观看和“吃”相关的视频的时候,可能会因人体的条件反射导致胃酸分泌量增加,然而这个时候人们可能并没有真正进食。再加上深夜的时候,距离吃完晚饭已经有一段时间,胃部的食物已经快要消化完毕,这个时候如果再有较多的胃酸分泌,就有可能诱发或者加重胃部疾病。
声明:本文所阐述的观点仅供参考,本文所得出的结论仅仅是思想实验的可能结果,没有经过实验验证。
观看和“吃”相关的视频的时候,可能会因人体的条件反射导致胃酸分泌量增加,然而这个时候人们可能并没有真正进食。再加上深夜的时候,距离吃完晚饭已经有一段时间,胃部的食物已经快要消化完毕,这个时候如果再有较多的胃酸分泌,就有可能诱发或者加重胃部疾病。
根据 Google 博客的消息(原文地址:https://www.blog.google/products/android/evolving-android-brand/),包括手机,汽车,手表,电视等设备在内,全球范围内搭载 Android 系统的设备已经超过 25 亿台。为了使 Android 发展得更好,Google 方面最近采取了两项措施。
在之前的发行版中,Google 的工程师会给每个发行版起一个内部代码名字,这个名字通常是按首字母顺序依次使用的美味的点心或者甜品的名称。这么做虽然很有趣,但是根据过去几年的反馈,并不是每个人都能理解这些名字的含义,因为 Android 在世界各个地方都有开发者,这些开发者之间有着许多语言和文化上的差异。例如,在一些语言中是不区分 “L” 和 “R” 的,因此,习惯于使用这些语言的人们就不能直观地理解 “Android Lollipop” 是 “Android KitKat” 之后的一个版本。同样的困扰也可能存在于 Android 的使用者身上,由于有些用户可能不了解 Android 的命名惯例,因此就难以判断自己的设备上运行的 Android 系统是不是最新版的。此外,在一些地方,”pies” 并不是指的甜点,而且虽然棉花糖 (marshmallows) 很美味,但并不是世界上所有地方都流行吃棉花糖。
作为一个全球性的操作系统,对人们来说,一个清晰直观的名字是很重要的。因此,从下一个版本的 Android 系统开始,将使用简单直接的数字来命名,而下一个版本的 Android 被命名为 “Android 10”.

Android 系统的 LOGO 已经变化了很多次了,此次对 LOGO 的修改更多地考虑到使其更加“无障碍化”,因为对于 Android 开发者社区中一些有视觉障碍的人们而言,绿色的图标可能比较难以分辨。于是 Google 这次将 LOGO 中的 “Android” 变成了黑色的。
EOF
$\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $(\frac{\sin x}{1+\cos x}$ $+$ $|x|)$ $dx$ $=$__.
本题存在(关于原点对称的)对称区间 “$[-\frac{\pi}{2}$, $\frac{\pi}{2}]$”, 在求积分的时候,如果看到这样的对称区间,则要考虑被积函数是不是奇函数或者偶函数。如果是奇函数,则其在对称区间上的积分为 $0$, 如果是偶函数,则我们可以只计算其大于 $0$ 或者小于 $0$ 方向上的积分,之后再乘以 $2$ 即可获得整个积分区间上的积分数值。
由于:
$\frac{\sin (-x)}{1+\cos(-x)}$ $=$ $\frac{-\sin x}{1+\cos x}$ $\Rightarrow$ $f(-x)$ $=$ $-f(x)$.
因此,$f(x)$ $=$ $\frac{\sin x}{1+\cos x}$ 是一个奇函数,因此,其在对称区间 $[-\frac{\pi}{2}$, $\frac{\pi}{2}]$ 上的积分为 $0$.
又由于:
$|-x|$ $=$ $|x|$ $\Rightarrow$ $g(-x)$ $=$ $g(x)$.
因此,$g(x)$ $=$ $|x|$ 是一个偶函数。
于是:
原式 $=$ $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $|x|$ $dx$ $=$ $2$ $\int_{0}^{\frac{\pi}{2}}$ $x$ $dx$ $=$ $2$ $\cdot$ $\frac{1}{2}x^{2}|_{0}^{\frac{\pi}{2}}$ $=$ $\frac{\pi^{2}}{4}$.
当然,本题除了可以使用积分的原理计算之外,还可以画图计算面积,如图 1:
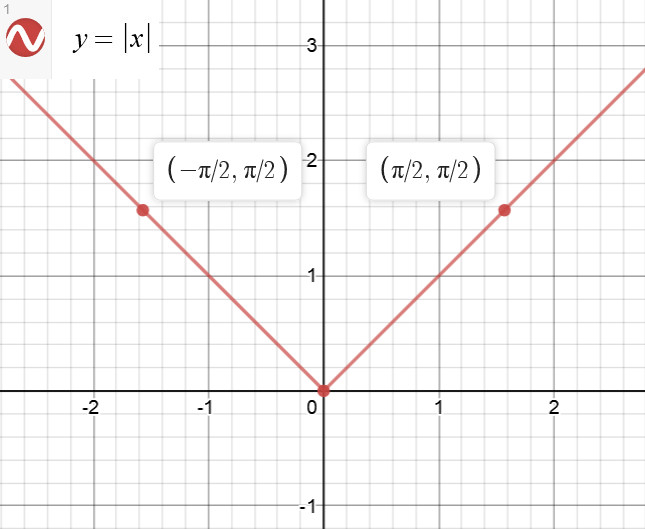
根据上图,我们有:
$\frac{\pi}{2}$ $\cdot$ $\frac{\pi}{2}$ $\cdot$ $\frac{1}{2}$ $\cdot$ $2$ $=$ $\frac{\pi^{2}}{4}$.
综上可知,本题的正确答案是:$\frac{\pi^{2}}{4}$.
EOF
$\lim_{x \rightarrow 0}$ $(\frac{1-\tan x}{1+\tan x})^{\frac{1}{\sin kx}}$ $=$ $e$, 则 $k$ $=$__.
观察本题可以发现,这是一个求极限的式子,而且等式的右边是 $e$, 符合“两个重要极限”中的第二个重要极限的一部分特征。
两个重要极限如下:
$\lim_{x \rightarrow x_{x_{0}}}$ $\frac{\sin x}{x}$ $=$ $1$, $\lim_{x \rightarrow 0}$ $(1+x)^{\frac{1}{x}}$ $=$ $\lim_{x \rightarrow \infty}$ $(1+\frac{1}{x})^{x}$ $=$ $e$.
由于题目中的式子不存在上述公式中的 $1$, 因此,我们需要构造出这个 $1$, 即:
$1$ $+$ $\square$ $=$ $\frac{1-\tan x}{1+\tan x }$ $\Rightarrow$ $\square$ $=$ $\frac{1-\tan x}{1+\tan x}$ $-$ $1$ $=$ $\frac{1-\tan x}{1+\tan x}$ $-$ $\frac{1+\tan x}{1+\tan x}$ $=$ $\frac{-2 \tan x}{1+\tan x}$.
于是,原式 $=$ $\lim_{x \rightarrow 0}$ $(1+\frac{-2\tan x}{1+\tan x})^{\frac{1}{\sin kx}}$ $=$ $e$. (1)
由于当 $x$ $\rightarrow$ $0$ 时,$\frac{-2\tan x}{1+\tan x}$ $\rightarrow$ $0$ 且 $\frac{1}{\sin kx}$ $\rightarrow$ $\infty$, 所以,符合使用“两个重要极限”的条件,可以继续接下来的计算。
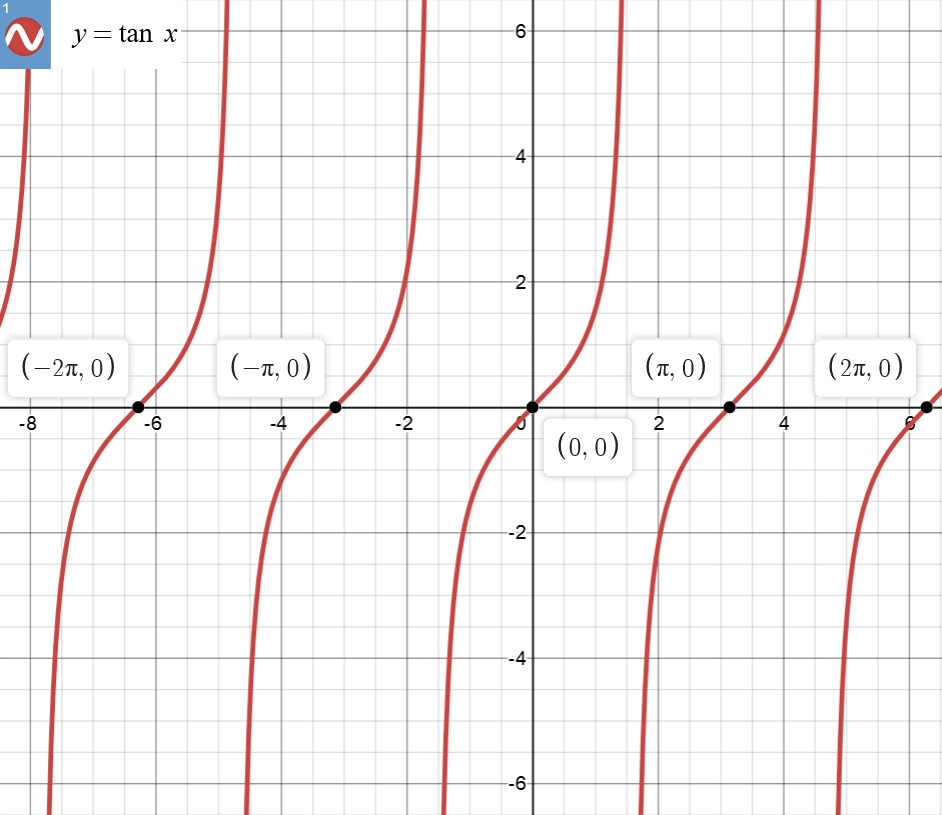
接下来继续向公式的方向构造等式。
$(1)$ $=$ $\lim_{x \rightarrow 0}$ $(1+\frac{-2\tan x}{1+\tan x})^{\frac{1+\tan x}{-2\tan x} \frac{-2\tan x}{1+\tan x} \frac{1}{\sin kx}}$. (2)
根据公式,我们知道:
$\lim_{x \rightarrow 0}$ $(1+\frac{-2\tan x}{1+\tan x})^{\frac{1+\tan x}{-2\tan x}}$ $=$ $e$.
于是:
$(2)$ $=$ $e^{\lim_{x \rightarrow 0} \frac{-2\tan x}{1+\tan x}\frac{1}{\sin kx}}$ $=$ $e^{\lim_{x \rightarrow 0} \frac{-2\tan x}{(1+\tan x)\sin kx}}$. (3)
当 $x$ $\rightarrow$ $0$ 时,$\tan x$ $\rightarrow$ $0$ 是不可以带入原式中的(只有非零和非无穷的数值可以带入原式中。),不过当 $x$ $\rightarrow$ $0$ 时,$(1+\tan x)$ $\rightarrow$ $1$ 是可以带入原式中的,于是:
$\lim_{x \rightarrow 0}$ $\frac{-2\tan x}{(1+\tan x)\sin kx}$ $=$ $\lim_{x \rightarrow 0}$ $\frac{-2\tan x}{\sin kx}$.
又因为当 $x$ $\rightarrow$ $0$ 时,$\sin x$ $\sim$ $\tan x$ $\sim x$, 于是:
$\lim_{x \rightarrow 0}$ $\frac{-2\tan x}{\sin kx}$ $=$ $\lim_{x \rightarrow 0}$ $\frac{-2x}{kx}$ $=$ $-\frac{2}{k}$.
即:
$e^{-\frac{2}{k}}$ $=$ $e$ $\Rightarrow$ $-$ $\frac{2}{k}$ $=$ $1$ $\Rightarrow$ $k$ $=$ $-$ $2$.
综上可知,正确答案是:$-2$.
EOF
设函数 $f(x)$ $=$ $x$ $+$ $a$ $\ln(1+x)$ $+$ $bx$ $\sin x$, $g(x)$ $=$ $k$ $x^{3}$ 在 $x$ $\rightarrow$ $0$ 时等价无穷小,求常数 $a$, $b$, $k$ 的取值.
由于 $x$ $\rightarrow$ $0$ 时,$f(x)$ 和 $g(x)$ 是等价无穷小,因此有:
$\lim_{x \rightarrow 0}$ $\frac{f(x)}{g(x)}$ $=$ $1$, 即:
$\lim_{x \rightarrow 0}$ $\frac{x+a \ln(1+x) + bx \sin x}{kx^{3}}$ $=$ $1$.
又由麦克劳林公式:
1. $\sin x$ $=$ $x$ $+$ $o(x^{2})$;
注 1:
根据麦克劳林公式,$\sin x$ 也可以等于 $x$ $-$ $\frac{x^{3}}{6}$ $+$ $o(x^{4})$, 但是这里为了能够在接下来的计算中使得分子分母可以使用“对照”的方式求解,分子的最大幂次不能大于分母的最大幂次。由于 $\sin x$ 在使用麦克劳林公式替换之后还需要和 $x$ 相乘得到二次幂,因此这里只能令 $\sin x$ 等于 $x$ $+$ $o(x^{2})$.
2. $\ln(1+x)$ $=$ $x$ $-$ $\frac{x^{2}}{2}+\frac{x^{3}}{3}$ $+$ $o(x^{3})$.
注 2:
对 $\ln(1+x)$ 项数的选取所依据的原因和注 $1$ 一致。
于是,我们有:
$1$ $=$ $\lim_{x \rightarrow 0}$ $\frac{x+ax-\frac{a}{2}x^{2}+\frac{a}{3}x^{3}+o(x^{3})+bx^{2}+o(x^{3})}{kx^{3}}$ $=$ $\lim_{x \rightarrow 0}$ $\frac{(1+a)x+(b-\frac{a}{2})x^{2}+\frac{a}{3}x^{3}+o(x^{3})}{kx^{3}}$.
于是,我们有:
$\left\{\begin{matrix} 1+a=0,\\ b-\frac{a}{2}=0,\\ \frac{a}{3}=k. \end{matrix}\right.$
解得:
$\left\{\begin{matrix} a=-1,\\ b=-\frac{1}{2},\\ k=-\frac{1}{3}. \end{matrix}\right.$

EOF

如果从 1969 年 NASA 的航天器成功登陆月球开始算起,今年是阿波罗计划 50 周年。
在 1971 年的 07 月 31 日,阿波罗 15 号任务首次在月球使用了月球漫游车。这是一台轻量级的车,使用电力驱动,可以在月球表面的低重力真空环境中行驶,帮助宇航员探索着陆点周围的环境。
本文中的这张照片是在阿波罗 15 号任务中宇航员第三次出舱活动时拍摄的,照片的背景是荒凉的月球和无穷无尽的深空。然而,当人类的脚步开始点缀在这颗星球上时,她的美便开始难以用语言形容。
更多信息可以访问:
https://www.nasa.gov/centers/marshall/history/index.html
微分方程 $y”$ $+$ $2y’$ $+$ $3y$ $=$ $0$ 的通解为__.
观察可知,这是一个二阶常系数线性齐次微分方程。
二阶常系数线性齐次微分方程的性质如下:
形如 $y”$ $+$ $py’$ $+$ $qy$ $=$ $0$, 其中 $p$, $q$ 均为常数。
特征方程为:$\lambda^{2}$ $+$ $p$ $\lambda$ $+$ $q$ $=$ $0$,
(1) 当 $\lambda_{1}$, $\lambda_{2}$ 为互异实根时,微分方程得通解为 $y(x)$ $=$ $C_{1}$ $e^{\lambda_{1}x}$ $+$ $C_{2}$ $e^{\lambda_{2}x}$;
(2) 当 $\lambda_{1}$ $=$ $\lambda_{2}$ 时,通解为 $y(x)$ $=$ $(C_{1}+C_{2}x)$ $e^{\lambda_{1}x}$;
(3) 当 $\lambda$ $=$ $\alpha$ $\pm$ $i$ $\beta$ (复数根)时,通解为 $y(x)$ $=$ $e^{\alpha x}$ $(C_{1}$ $\cos \beta$ $x$ $+$ $C_{2}$ $\sin \beta$ $x)$.
在本题中,特征方程中的 $p$ $=$ $2$, $q$ $=$ $3$, 因此特征方程为:
$\lambda^{2}$ $+$ $2$ $\lambda$ $+$ $3$ $=$ $0$. (1)
此外,我们还知道,对于形如 $a$ $x^{2}$ $+$ $bx$ $+$ $c$ $=0$ 的一元二次方程,其求根公式为:
$x$ $=$ $\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}$.
于是,我们知道,对于 (1) 式:
$\lambda$ $=$ $\frac{-2\pm\sqrt{4-12}}{2}$ $=$ $\frac{-2\pm\sqrt{-8}}{2}$. (2)
我们又知道,在虚数中(复数包含虚数和实数),虚数单位 $i$ 有如下性质:
$i^{2}$ $=$ $-1$.
于是,(2) 式可以写成:
$\lambda$ $=$ $\frac{-2\pm\sqrt{8i^{2}}}{2}$ $=$ $\frac{-2\pm i 2 \sqrt{2}}{2}$ $=$ $-1$ $\pm$ $i$ $\sqrt{2}$.
于是,$\alpha$ $=$ $-1$, $\beta$ $=$ $\sqrt{2}$.
因此,正确答案是:
$y$ $=$ $e^{-x}$ $(C_{1}$ $\cos \sqrt{2}x$ $+$ $C_{2}$ $\sin \sqrt{2}$ $x$ $)$
EOF
微分方程 $xy’$ $+$ $y$ $=0$ 满足条件 $y(1)$ $=$ $1$ 的解是 $y$ $=$__.
由 $xy’$ $+$ $y$ $=0$ 得:
$(xy)’$ $=0$.
即:
$xy$ $=$ $C$ $\Rightarrow$ $y$ $=$ $\frac{C}{x}$
又因为 $y(1)$ $=$ $1$ $\Rightarrow$ $1$ $=$ $\frac{C}{1}$ $\Rightarrow$ $C$ $=$ $1$ $\Rightarrow$ $y$ $=$ $\frac{1}{x}$.
综上可知,正确答案是:$\frac{1}{x}$.
EOF
设有两个数列 ${a_{n}}$, ${b_{n}}$, 若 $\lim_{n \rightarrow \infty}$ $a_{n}$ $=0$, 则()
( A ) 当 $\sum_{n=1}^{\infty}$ $b_{n}$ 收敛时,$\sum_{n=1}^{\infty}$ $a_{n}$ $b_{n}$ 收敛.
( B ) 当 $\sum_{n=1}^{\infty}$ $b_{n}$ 发散时,$\sum_{n=1}^{\infty}$ $a_{n}$ $b_{n}$ 发散.
( C ) 当 $\sum_{n=1}^{\infty}$ $|b_{n}|$ 收敛时,$\sum_{n=1}^{\infty}$ $a_{n}^{2}$ $b_{n}^{2}$ 收敛.
( D ) 当 $\sum_{n=1}^{\infty}$ $|b_{n}|$ 发散时,$\sum_{n=1}^{\infty}$ $a_{n}^{2}$ $b_{n}^{2}$ 发散.
由题目信息可知,当 $n$ $\rightarrow$ $\infty$ 时,数列 ${a_{n}}$ 是收敛的。
A 项:
令 $a_{n}$ $=$ $b_{n}$ $=$ $(-1)^{n-1}$ $\frac{1}{\sqrt{n}}$.
则此时 ${a_{n}}$ 是一个收敛数列,$\sum_{n=1}^{\infty}$ $b_{n}$ 也收敛(根据交错级数的莱布尼茨准则判别法可得此结论),但 $\sum_{n=1}^{\infty}$ $a_{n}$ $b_{n}$ $=$ $\sum_{n=1}^{\infty}$ $\frac{1}{n}$ 发散(由常见级数的敛散性可得此结论)。
由此构成了对 A 项的反例,A 项错误。
注 1. 交错级数 $\sum_{n=1}^{\infty}$ $(-1)^{n-1}u_{n}$ $(u_{n}>0)$ 的判别法(莱布尼茨准则):
若交错级数 $\sum_{n=1}^{\infty}$ $(-1)^{n-1}u_{n}$ $(u_{n}>0)$ 满足如下条件:
① $u_{n}$ $\geqslant$ $u_{n+1}$, $(n = 1,2,3, \dotsc)$;
② $\lim$ $u_{n}$ $=$ $0$,
则交错级数收敛,其和 $S$ $\leqslant$ $u_{1}$, 余项 $|R_{n}|$ $\leqslant$ $u_{n+1}$.
注 2. 常见级数的敛散性:
$p$ 级数 $\sum_{n=1}^{\infty}$ $\frac{1}{n^{p}}$ $\left\{\begin{matrix} 收敛 & p>1,\\ 发散 & p \leqslant 1. \end{matrix}\right.$
B 项:
令 $a_{n}$ $=$ $b_{n}$ $=$ $\frac{1}{n}$, 则
$\sum_{n=1}^{\infty}$ $a_{n}$ $b_{n}$ $=$ $\sum_{n=1}^{\infty}$ $\frac{1}{n^{2}}$.
此时,数列 ${a_{n}}$ 是一个收敛数列,$\sum_{n=1}^{\infty}$ $b_{n}$ 是发散的,但是 $\sum_{n=1}^{\infty}$ $\frac{1}{n^{2}}$ 是收敛的。
由此构成了对 B 项的反例,B 项错误。
D 项:
和 B 项一样,令 $a_{n}$ $=$ $b_{n}$ $=$ $\frac{1}{n}$, 则 $\sum_{n=1}^{\infty}$ $a_{n}^{2}$ $b_{n}^{2}$ $=$ $\sum_{n=1}^{\infty}$ $\frac{1}{n^{4}}$ 是收敛的。
由此构成了对 D 项的反例,D 项错误。
综上可知,排除了 A, B, D 三个选项后,正确选项一定是 C 项。
我们可以使用级数收敛的必要条件直接证明 C 项正确。
级数 $\sum_{n=1}^{\infty}$ $u_{n}$ 收敛的必要条件:$\lim_{n \rightarrow \infty}$ $u_{n}$ $=$ $0$.
由于 $\lim_{n \rightarrow \infty}$ $u_{n}$ $=$ $0$ 是级数 $\sum_{n=1}^{\infty}$ $u_{n}$ 收敛的必要条件,因此,根据“小充分大必要”的原则,我们知道:
$\sum_{n=1}^{\infty}$ $u_{n}$ 收敛 $\Rightarrow$ $\lim_{n \rightarrow \infty}$ $u_{n}$ $=$ $0$;
$\lim_{n \rightarrow \infty}$ $u_{n}$ $=$ $0$ $\nRightarrow$ $\sum_{n=1}^{\infty}$ $u_{n}$ 收敛。
由于 $\lim_{n \rightarrow \infty}$ $a_{n}$ $=$ $0$, 从而存在 $M$ $>$ $0$, 有 $|a_{n}|$ $\leqslant$ $M$, 即:
$a_{n}^{2}$ $b_{n}^{2}$ $\leqslant$ $M^{2}$ $b_{n}^{2}$. 又因为 $\sum_{n=1}^{\infty}$ $|b_{n}|$ 收敛,故有:
$\lim_{n \rightarrow \infty}$ $|b_{n}|$ $=0$.
又根据如下定理:
设 $c$ 为非零常数,则 $\sum_{n=1}^{\infty}$ $u_{n}$ 与 $\sum_{n=1}^{\infty}$ $cu_{n}$ 具有相同的敛散性。
因此,$\sum_{n=1}^{\infty}$ $M^{2}$ $|b_{n}|$ 收敛,即:
$\lim_{n=1}^{\infty}$ $M^{2}$ $|b_{n}|$ $=$ $0$.
于是:
$\lim_{n \rightarrow \infty}$ $\frac{M^{2}|b_{n}||b_{n}|}{|b_{n}|}$ $=$ $\lim_{n \rightarrow \infty}$ $M^{2}$ $|b_{n}|$ $=$ $\lim_{n \rightarrow \infty}$ $\frac{M^{2}b_{n}^{2}}{|b_{n}|}$ $=$ $0$.
接下来,根据“比较判别法的极限形式”:
设 $\sum_{n=1}^{\infty}$ $u_{n}$ 与 $\sum_{n=1}^{\infty}$ $v_{n}$ 均为正项级数,且 $\lim_{n \rightarrow \infty}$ $\frac{u_{n}}{v_{n}}$ $=$ $A(v_{n} \neq 0)$.
① 若 $0$ $\leqslant$ $A$ $\leqslant$ $+$ $\infty$, 且 $\sum_{n=1}^{\infty}$ $v_{n}$ 收敛,则 $\sum_{n=1}^{\infty}$ $u_{n}$ 收敛.
② 若 $0$ $\leqslant$ $A$ $\leqslant$ $+$ $\infty$, 且 $\sum_{n=1}^{\infty}$ $v_{n}$ 发散,则 $\sum_{n=1}^{\infty}$ $u_{n}$ 发散.
于是我们知道,$\sum_{n=1}^{\infty}$ ${M^{2} b_{n}^{2}}$ 收敛。
又因为 $a^{2}$ $b^{2}$ $\leqslant$ $M^{2}$ $b^{2}$, 所以:
$\sum_{n=1}^{\infty}$ ${a^{2} b_{n}^{2}}$ 收敛.
由此得证 C 项正确。
EOF
设 $M$ $=$ $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $\frac{(1+x)^{2}}{1+x^{2}}$ $dx$, $N$ $=$ $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $\frac{1+x}{e^{x}}$ $dx$, $K$ $=$ $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $(1+\sqrt{\cos x})$ $dx$, 则 ( )
( A ) $M$ $>$ $N$ $>$ $K$
( B ) $M$ $>$ $K$ $>$ $N$
( C ) $K$ $>$ $M$ $>$ $N$
( D ) $K$ $>$ $N$ $>$ $M$
在解答题目时,能化简的要先化简,能计算出具体数值的要先计算出具体数值。
首先观察本题,发现 $M$ 对应的式子应该是可以化简或者通过积分计算出具体的数值。于是:
$M$ $=$ $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $\frac{(1+x)^{2}}{1+x^{2}}$ $dx$ $=$ $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $\frac{1+x^{2}+2x}{1+x^{2}}$ $dx$ $=$ $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $[\frac{1+x^{2}}{1+x^{2}}$ $+$ $\frac{2x}{1+x^{2}}]$ $dx$ $=$ $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $[$ $1$ $+$ $\frac{2x}{1+x^{2}}]$ $dx$
计算到上面这一步之后,我们有两种方法可以继续上面的计算,一种方法是利用积分函数在对称区间上的性质,另一种是利用基本积分公式直接计算。
下面分别使用上述提到的两种方法展开计算。
方法一:利用积分函数在对称区间上的性质
这里说的“对称区间”指的是关于原点对称的区间,观察题目可知,题目中的积分函数的上限和下限组成的区间 $[-\frac{\pi}{2}$, $\frac{\pi}{2}]$ 正好是关于原点对称的。
根据积分的几何意义,我们知道,奇函数在关于原点对称的对称区间上的积分是等于 $0$ 的。
$y$ $=$ $x$, $x$ $\in$ $(-\infty,$ $+\infty)$ 就是一个典型的奇函数,如图 1:
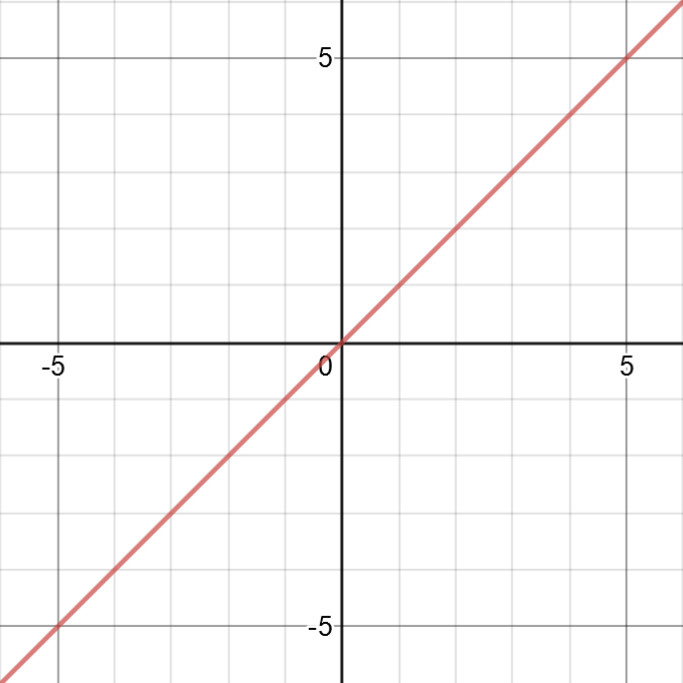
因此,接下来,我们如果能证明一个函数是奇函数,就可以证明这个函数在关于原点对称的区间上的积分是 $0$.
于是,令:
$f(x)$ $=$ $\frac{2x}{1+x^{2}}$
则:
$\frac{2(-x)}{1+(-x)^{2}}$ $=$ $-\frac{2x}{1+x^{2}}$ $\Rightarrow$ $f(-x)$ $=$ $-f(x)$.
因此 $f(x)$ $=$ $\frac{2x}{1+x^{2}}$ 是一个奇函数,于是:
$\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $\frac{2x}{1+x^{2}}$ $dx$ $=$ $0$.
即:
$M$ $=$ $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $1$ $dx$.
方法二:利用基本积分公式直接计算
由前面的计算,我们已知,$M$ $=$ $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $\frac{2x}{1+x^{2}}$ $dx$, 于是,根据积分公式:
$d(x^{\mu})$ $=$ $\mu$ $x^{\mu-1}$ $dx$
我们可以令 $2x$ $dx$ $=$ $d(1+x^{2})$.
于是:
$M$ $=$ $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $1$ $dx$ $+$ $\frac{d(1+x^{2})}{1+x^{2}}$ $=$ $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $1$ $dx$ $+$ $\frac{1}{1+x^{2}}$ $d(1+x^{2})$.
接下来,根据基本积分公式:
$\int$ $\frac{1}{x}$ $dx$ $=$ $\ln |x|$ $+$ $c$.
我们有:
$M$ $=$ $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $1$ $+$ $\frac{1}{1+x^{2}}d(1+x^{2})$ $=$ $x$ $+$ $\ln |1+x^{2}|$ $+$ $c$ $|_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $=$ $\frac{\pi}{2}$ $+$ $|\ln[1+(\frac{\pi}{2})^{2}]|$ $+$ $c$ $-$ $(-\frac{\pi}{2})$ $-$ $|\ln[1+(-\frac{\pi}{2})^{2}]|$ $-$ $c$ $=$ $\frac{\pi}{2}+\frac{\pi}{2}$ $=$ $\pi$.
又因为,$M$ 的积分上限 $\frac{\pi}{2}$ 减去 $M$ 的积分下限 $-\frac{\pi}{2}$ 也等于 $\pi$.
根据定积分的基本性质:
$\int_{a}^{b}$ $1$ $dx$ $=$ $b$ $-$ $a$.
我们知道:
$M$ $=$ $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $1$ $dx$.
补充:
如果是计算 $\int$ $\frac{2x}{1-x^{2}}$ $dx$, 则我们至少有以下两种计算方法:
$\int$ $\frac{2x}{1-x^{2}}$ $dx$ $=$ $-\int$ $\frac{1}{1-x^{2}}$ $=$ $-\ln |1-x^{2}|$ $+$ $c$;
或者:
$\int$ $\frac{2x}{1-x^{2}}$ $dx$ $=$ $\int$ $(\frac{1}{1-x}-\frac{1}{1+x})$ $dx$ $=$ $-\ln|x-1|$ $-$ $\ln|x+1|$ $+$ $c$ $=$ $-\ln|x^{2}-1|$ $+$ $c$.
至此,我们分别使用两种方法完成了对 $M$ 的化简计算。
根据定积分的比较定理:
设 $f(x)$ $\leqslant$ $g(x)$, $x$ $\in$ $[a,b]$, 则 $\int_{a}^{b}$ $f(x)$ $dx$ $\leqslant$ $\int_{a}^{b}$ $g(x)$ $dx$.
观察题目可知,题目中给出的三个定积分 $M$, $N$, $K$ 的上限和下限都是一样的,因此,我们可以使用上述比较定理比较他们的大小。
由于在 $M$, $N$, $K$ 中,我们目前已知的只有 $M$ 的数值,因此接下来我们先比较 $N$ 和 $K$ 中的积分函数与 $1$ 的大小关系。
首先来判断 $N$ 的积分函数和 $1$ 的大小关系。
当 $x$ $=$ $0$ 时,$1$ $+$ $x$ $=$ $e^{x}$ $=1$;
当 $x$ $<$ $0$ 时,$e^{x}$ 的减小速度小于 $1$ $+$ $x$ 的减小速度;
当 $x$ $>$ $0$ 时,$e^{x}$ 的增长速度大于 $1$ $+$ $x$ 的增长速度。
也就是说,在整个定义域内,$y$ $=$ $e^{x}$ 的函数图像始终在 $y$ $=$ $1$ $+$ $x$ 的上方或者和 $y$ $=$ $1$ $+$ $x$ 重合,他们二者的图像如图 2:
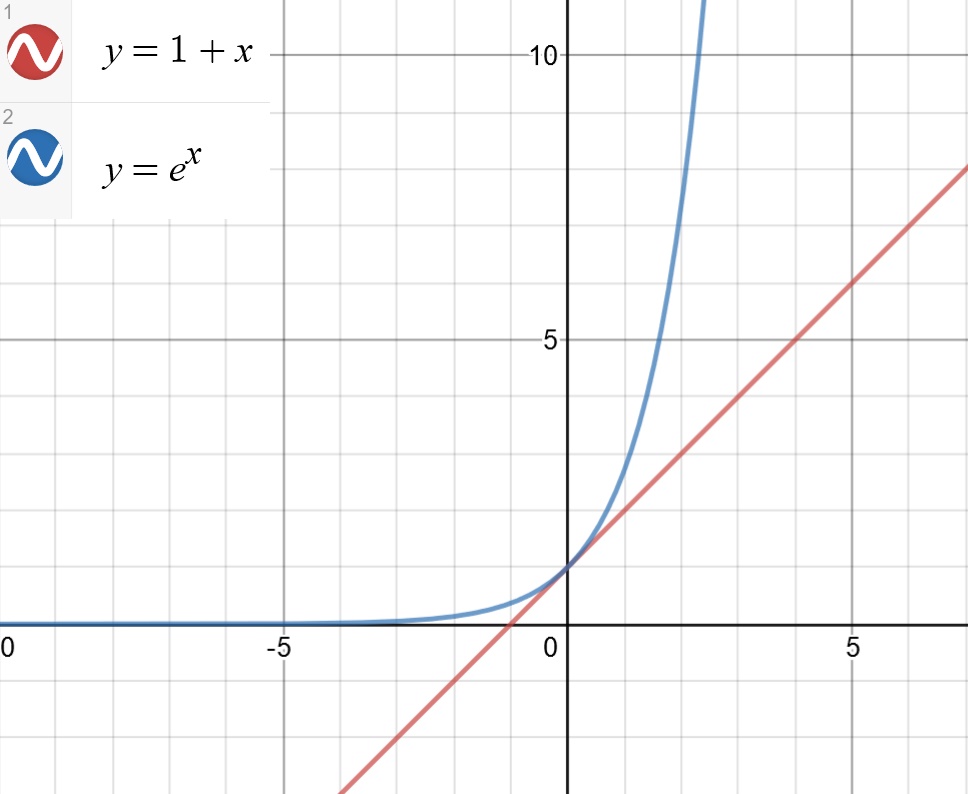
所以 $\frac{1+x}{e^{x}}$ $\leqslant$ $1$, $x$ $\in$ $[-\frac{\pi}{2}$, $\frac{\pi}{2}]$. 再来判断 $K$ 的积分函数和 $1$ 的大小关系。
我们知道,当 $x$ $\in$ $[$ $-\frac{\pi}{2},$ $\frac{\pi}{2}$ $]$ 上时,$y$ $=$ $\cos x$ $\geqslant$ $0$ 的,如图 3:
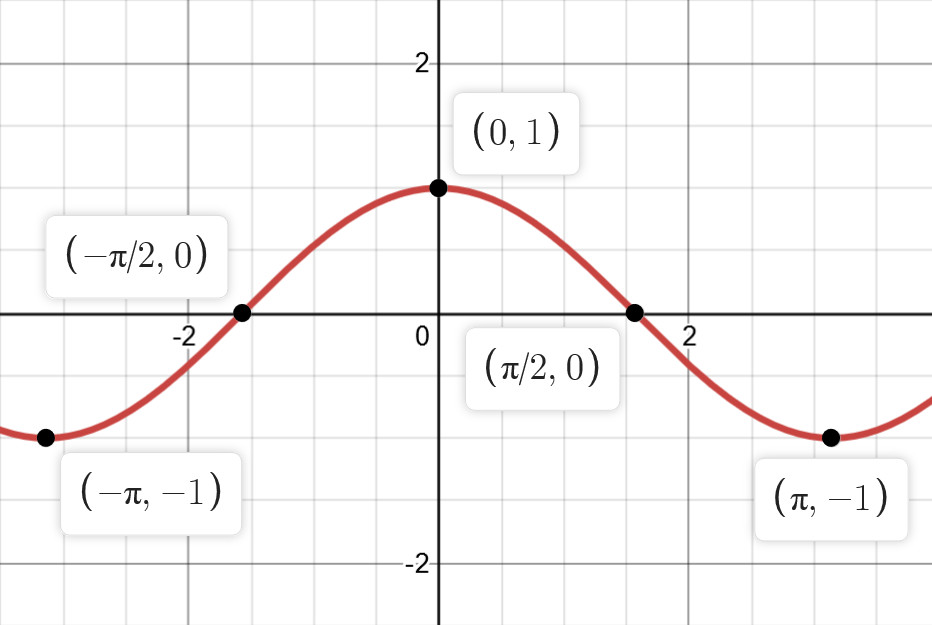
于是 $1$ $+$ $\sqrt{\cos x}$ $\geqslant$ $1$.
综上可知:
$K$ $\geqslant$ $M$ $\geqslant$ $N$, 正确选项是:C
EOF
2019 年 08 月 13 日,新版本的 XAMPP 发布,此次发布的安装程序包含以下组件:
本文消息来源:https://www.apachefriends.org/blog/new_xampp_20190813.html
XAMPP 官方下载地址:https://www.apachefriends.org/download.html
2019 年 08 月 13 日,WordPress.com 的母公司 Automattic 在其官方推特上宣布 Tumblr 已经加入 Automattic:
根据有关消息,这次收购的价格是 300 万美元。以下是在此之前 Tumblr 的部分发展历程:
2007 年 02 月,Tumblr 正式上线;
2016 年,Tumblr 的月访问量达到 5.5 亿;
2013 年,Tumblr 被雅虎以 11 亿美元收购;
2017 年,Tumblr 又被 Verizon 收购;
2018 年,Tumblr 开始限制站内的成人内容,此后网站访问量明显降低。
Tumblr 的创始人之一 Matt Mullenweg 在其位于 Tumblr 的博客上发文表示:
I look forward to working with everyone from Tumblr as we welcome them to Automattic, and I can’t wait for us to build great products together.
https://photomatt.tumblr.com/post/186964618222/automattic-tumblr
之后,他还在自己的个人网站 ma.tt 上发表了自己对个这个收购价格的看法:
First, they chose to find a new home for Tumblr instead of shutting it down. Second, they considered not just how much cash they would get on day one, but also — and especially — what would happen to the team afterward, and how the product and the team would be invested in going forward. Third, they thought about the sort of steward of the community the new owner would be. They didn’t have to do any of that, and I commend them for making all three points a priority.
https://ma.tt/2019/08/tumblr-the-day-after/
Automattic 旗下的 WordPress 和 Tumblr 都是博客平台,就我个人的感受而言,WordPress 是一个更侧重桌面端的博客平台,而 Tumblr 则是一个更侧重手机端的博客平台。因此,此次收购应该可以在未来起到优势互补的作用。
EOF
截至北京时间 2019 年 08 月 15 日晚间,CentOS 8 的构建进度表如下:
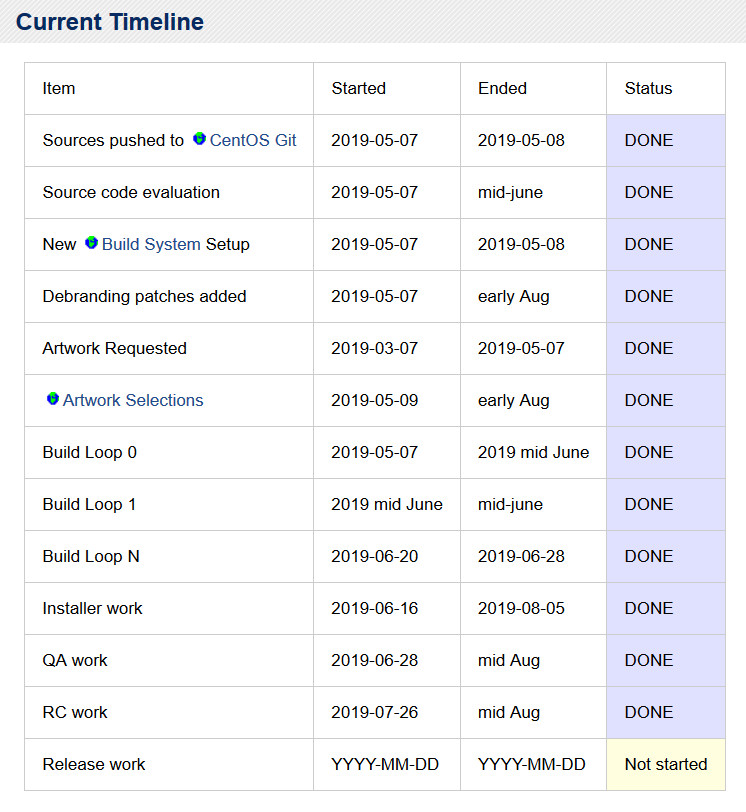
根据这个进度表,我们可以看到,CentOS 8 发布之前的各项开发工作基本已经全部完成,只剩最后的发布工作了。预计在八月底之前,CentOS 8 就将正式发布。
EOF
2019 年 08 月 05 日,中国开源云联盟发布了“木兰宽松许可证 (MulanPSL)” 第一版。根据已知消息,这应该是中国首个开源许可协议。木兰宽松许可证包含中文和英文两个版本,这两个版本具备相同的法律效力。
继续阅读“中国开源云联盟发布中国首个开源许可协议:木兰宽松许可证”设函数在 $f(x)$ 在 $(- \infty, + \infty)$ 内单调有界,${x_{n}}$ 为数列,下列命题正确的是 ( )
( A ) 若 ${x_{n}}$ 收敛,则 ${f(x_{n})}$ 收敛.
( B ) 若 ${x_{n}}$ 单调,则 ${f(x_{n})}$ 收敛.
( C ) 若 ${f(x_{n})}$ 收敛,则 ${x_{n}}$ 收敛.
( D ) 若 ${f(x_{n})}$ 单调,则 ${x_{n}}$ 收敛.
解答本题之前,我们需要清楚“极限”,“收敛”和“有界”三者之间的区别与联系。
当我们说“极限”时,我们通常说的是“函数极限”,当我们说“收敛”时,我们通常说的是“数列收敛”。说“数列收敛”就是说该数列存在极限。我们可以认为,“收敛”是用于描述离散数据的,“极限”是用于描述连续数据的。当我们在计算或者证明数列极限的时候,我们其实是将数列看作了“连续数据”来对待。
如果一个数列收敛,那么这个数列必然有界,但是如果一个数列有界却不一定收敛,例如下面这个数列有界,但不收敛:
$\{1,-1,1,-1,1,-1\}$.
对于函数也一样,例如 $y$ $=$ $\sin x$ 是一个有界函数,但不收敛。
只有单调并且有界的数列才一定收敛(也意味着该数列一定有极限),这就是数列极限的“单调有界原理”。
注:当“单调有界原理”用在数列上时可以证明数列有界;当单调有界原理用在函数上时只能证明函数有确界,即有上确界或者下确界。
此外,本题还涉及复合函数,因此还必须清楚复合函数的几个性质:
单调性包含单调递增和单调递减。对于复合函数而言,如果外函数和内函数都是单调函数,则在定义域内,它们的复合函数也是单调函数。至于是单调增还是单调减,可以用“同增异减”来判定。
“同增异减”的含义就是,如果外层函数是增函数,则复合函数的增减性与内函数的增减性一致;
如果外层函数为减函数,则复合函数的增减性与内函数的增减性相反。
“同增异减”也可以理解成,如果复合前两个函数都为增函数或者都为减函数,则复合函数为增函数;如果复合前两个函数一个为增函数,一个为减函数,则复合函数为减函数。
注:无论是单增还是单减,只要内函数和外函数都是单调函数,则复合函数也一定是单调函数。
① 如果内函数为奇函数,则复合函数的奇偶性与外函数的奇偶性保持一致;
② 如果内函数为偶函数,则复合函数必为偶函数。
① 若内函数为周期函数,则复合函数一定也是周期函数;
② 若外函数为周期函数,则复合函数不一定为周期函数。
① 若内函数有界且外函数有界,则复合函数一定有界;
② 若内函数无界但外函数有界,则复合函数一定有界;
(上述两条总结一下就是,无论内函数是否有界,只要外函数有界,则复合函数一定有界。)
③ 若内函数有界但外函数无界或者内外函数都无界,这种情况下不能确定或者否定复合函数是有界还是无界,如果要确定或否定,还需要其他条件辅助分析。
有上面的阐述,我们可以发现,在判断复合函数的性质的时候,第一步要做的事情就是区分出内函数和外函数。本题在内外函数的区分上可能具有一定的迷惑性,我们不能认为在复合函数 “${f(x_{n})}$” 中,”${x_{n}}$” 是外函数而 “$f(x)$” 是内函数,这是错误的。符号 “${$” 和 “$}$” 只是说明这是一个数列,而并不是一个运算符号,其意义是多个 “$f(x_{n})$” 的值组成的数列,因此外函数是 “$f(x)$”, 内函数是 “$x_{n}$.”
下面是针对每个选项的具体分析:
A 项:
${x_{n}}$ 收敛 → ${x_{n}}$ 有界;
$f(x)$ 有界 + ${x_{n}}$ 有界 → ${f(x_{n})}$ 有界;
但是数列有界不能直接推出数列收敛,必须是单调且有界的数列才能推出收敛的结论。
A 项错误。
B 项:
${x_{n}}$ 单调 + $f(x_{n})$ 单调 → ${f(x_{n})}$ 单调;
$f(x_{n})$ 有界 → ${f(x_{n})}$ 有界;
${f(x_{n})}$单调有界 → ${f(x_{n})}$ 收敛。
B 项正确。
C 项:
由复合函数收敛不能确定其内函数是否也收敛。
C 项错误。
D 项:
$f(x_{n})$ 有界 → ${f(x_{n})}$ 有界;
${f(x_{n})}$单调有界 → ${f(x_{n})}$ 收敛;
但是 ${f(x_{n})}$ 收敛推不出内函数 ${x_{n}}$ 也收敛,和 C 项原因一致。
D 项错误。
综上可知,正确选项是:B
EOF