题目
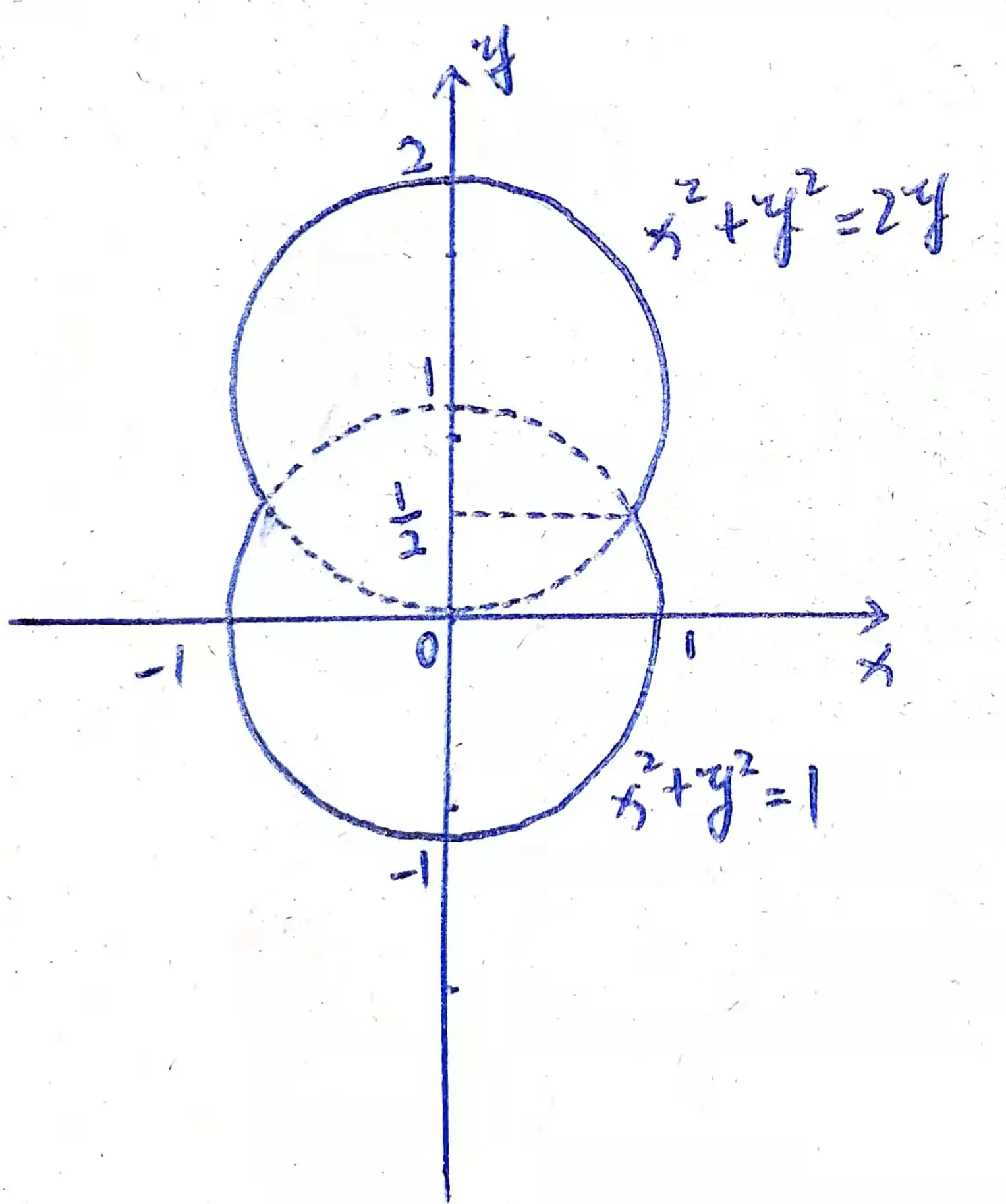
一容器的内侧是由图中曲线绕 $y$ 轴旋转一周而成的曲面,该曲线由 $x^{2} + y^{2} = 2y$ $ (y \geqslant \frac{1}{2})$ 与 $x^{2} + y^{2} = 1$ $(y \leqslant \frac{1}{2})$ 连接而成。
$(Ⅰ)$ 求容器的容积;
$(Ⅱ)$ 若将容器内盛满的水从容器顶部全部抽出,至少需要做多少功?
(长度单位:$m$, 重力加速度为 $g$ $ m/s^{2}$, 水的密度为 $10^{3}$ $kg/m^{3}$)
解析
第 $(Ⅰ)$ 问
方法一
由于该容器是关于 $y=\frac{1}{2}$ 对称的,因此,我们只需要求出该容器位于 $y=\frac{1}{2}$ 下面部分的体积,之后乘以 $2$ 即可。
由 $x^{2} + y^{2} = 1$, 得:
$$
x^{2} = 1 – y^{2} \Rightarrow
$$
$$
x(y) = \sqrt{1-y^{2}}.
$$
$$
V =
$$
$$
2 \pi \cdot \int_{-1}^{\frac{1}{2}} [x(y)]^{2} dy \Rightarrow
$$
$$
2 \pi \cdot \int_{-1}^{\frac{1}{2}} (1-y^{2}) dy \Rightarrow
$$
$$
2 \pi \cdot [y – \frac{1}{3} y^{3}]|_{-1}^{\frac{1}{2}} =
$$
$$
2 \pi \cdot [(\frac{1}{2} – \frac{1}{3} \cdot \frac{1}{8}) – (-1+\frac{1}{3})]=
$$
$$
\frac{9 \pi}{4}.
$$
方法二
根据题目可知,图 01 中的曲线是由如下两条曲线组成的:
$$
x(y) = \sqrt{1-y^{2}}, -1 \leqslant y \leqslant \frac{1}{2};
$$
$$
x(y) = \sqrt{2y – y^{2}}, \frac{1}{2} \leqslant y \leqslant 2.
$$
于是,我们有:
$$
V =
$$
$$
\pi \cdot [\int_{-1}^{\frac{1}{2}} (1-y^{2}) dy + \int_{\frac{1}{2}}^{2} (2y-y^{2}) dy] =
$$
$$ \pi \cdot [(y – \frac{1}{3} y^{3})|_{-1}^{\frac{1}{2}} + (y^{2} – \frac{1}{3} y^{3})|_{\frac{1}{2}}^{2}] = $$
$$
\pi \cdot [\frac{1}{2} – \frac{1}{3} \cdot \frac{1}{8} + 1 – \frac{1}{3} + 4 – \frac{8}{3} – \frac{1}{4} + \frac{1}{3} \cdot \frac{1}{8}] =
$$
$$
\frac{9 \pi}{4}.
$$
第 $(Ⅱ)$ 问
在这里,我们以 $y = \frac{1}{2}$ 为界,将题目所指的容器分为“上半部分”和“下半部分”两部分。
要从该容器的顶部将装满的水抽出,所需做功最少的方式就是以恒定的速率抽水,而以恒定的速率抽水就相当于恒力做工。恒力做工的公式如下:
$$
W = FS.
$$
注:
① $W$ 为“功”,$F$ 为“力”,$S$ 为力 $F$ 在力的方向上作用的“距离”;
② 当 $F$ 的计量单位为“牛顿”,$S$ 的计量单位为“米”的时候,$W$ 的计量单位为“焦耳”。
在本题中,由于我们要计算的这个容器是由曲线旋转而成的曲面组成的,因此,只能采用微分的方式“化曲为直”,因此,我们每次只抽取 “$dy$” 高度的水,对应所需做的功就是 “$dW$”.
又由水的密度 $\rho$, 重力加速度 $g$ 可知,该容器中,高度为 $dy$ 的水的质量 $m$,也就是抽出这段体积为 $V$ 的水所需的力 $F$ 为:
$$
F = m = \rho g V \Rightarrow
$$
$$
F = \rho g [ (\pi r^{2}) dy ].
$$
上式中的 “$r$”, 就对应于题目中的 $x$. 但是,由题可知,这个 “$x$” 需要两个公式来表示。如果我们将该容器上半部分涉及到的变量加上下角标 “$a$”, 将该容器下半部分涉及到的变量加上下角标 “$b$”, 则有:
$$
x^{2} + y^{2} = 2y \Rightarrow
$$
$$
x_{a}^{2} = 2y – y^{2};
$$
$$
x^{2} + y^{2} = 1 \Rightarrow
$$
$$
x_{b}^{2} = 1 – y^{2}.
$$
又由于,抽水操作是在该容器的顶部进行的,因此,在整个过程中,力 $F$ 在力的方向上作用的距离 $S$ 都可以用 $2-y$ 表示,即:
$$
S = 2-y.
$$
注:由于本问的计算过程中涉及到的变量 “$y$” 都是指直接位于 $Y$ 轴上的 $y$, 因此,不需要对变量 $y$ 区分是位于该容器上半部分的 $y$ 还是位于该容器下半部分的 $y$.
于是,在该容器的上半部分抽出高度为 $dy$ 的一小段水所需做的最少的功为:
$$
d W_{a} = \rho g \pi x_{a}^{2} dy \cdot (2-y) \Rightarrow
$$
$$
d W_{a} = \rho g \pi (2y – y^{2}) dy (2-y).
$$
同理,在该容器的下半部分抽出高度为 $dy$ 的一小段水所需做的最少的功为:
$$
d W_{b} = \rho g \pi x_{b}^{2} dy \cdot (2-y) \Rightarrow
$$
$$
d W_{b} = \rho g \pi (1-y^{2}) dy (2-y).
$$
于是,我们分别对 $d W_{a}$ 和 $d W_{b}$ 积分后,再求和,再代入从题目中可知的一些数值,即可求解此题。
$$
d W_{a} = \rho g \pi (2y – y^{2}) dy (2-y) \Rightarrow
$$
$$
\int_{\frac{1}{2}}^{2} W_{a} dy =
$$
$$
\int_{\frac{1}{2}}^{2} \rho g \pi (2y – y^{2}) (2-y) dy =
$$
$$
\rho g \pi \int_{\frac{1}{2}}^{2} (4y – 4y^{2} + y^{3}) dy =
$$
$$
\rho g \pi \cdot (2y^{2} – \frac{4}{3} y^{3} + \frac{1}{4} y^{4})|_{\frac{1}{2}}^{2} = (1-\frac{1}{64}) \rho g \pi.
$$
$$
d W_{b} = \rho g \pi (1-y^{2}) dy (2-y) \Rightarrow
$$
$$
\int_{-1}^{\frac{1}{2}} W_{b} dy =
$$
$$
\int_{-1}^{\frac{1}{2}} \rho g \pi (1-y^{2})(2-y) dy =
$$
$$
\rho g \pi \int_{-1}^{\frac{1}{2}} (2 – y – 2y^{2} + y^{3}) dy =
$$
$$
\rho g \pi \cdot (2y – \frac{1}{2}y^{2} – \frac{2}{3} y^{3} + \frac{1}{4}y^{4})|_{-1}^{\frac{1}{2}} = (\frac{19}{8} + \frac{1}{64}) \rho g \pi.
$$
于是,所需做的功为:
$$
(1 – \frac{1}{64} + \frac{19}{8} + \frac{1}{64}) \rho g \pi =
$$
$$
\frac{27 \cdot 10^{3}}{8} \pi g (焦耳).
$$