2012年考研数二第06题解析

题目

设区域 $D$ 由曲线 $y=\sin x$, $x=\pm \frac{\pi }{2}$, $y=1$ 围成，则 ${\iint }_D(x{y}^5–1)dxdy=?$

$$A.\pi$$

$$B.2$$

$$C.-2$$

$$D.-\pi$$

解析

方法一

对于二重积分，首先画出区域 $D$, 如图 1 所示：

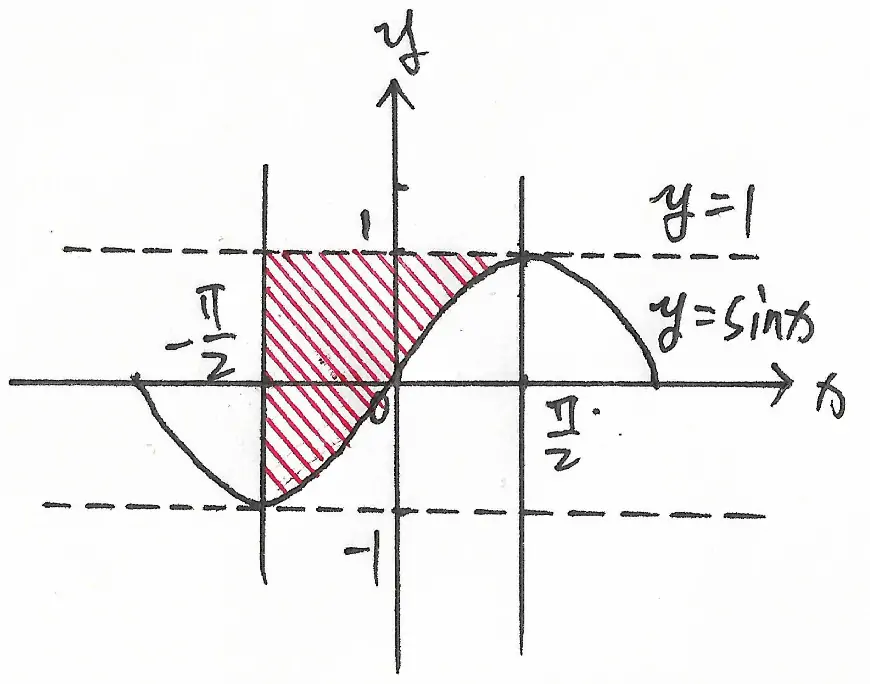
接着开始计算：

$${\iint }_D(x{y}^5–1)dxdy=$$

$${\iint }_D(x{y}^5)dxdy–{\iint }_{D}1dxdy\Rightarrow$$

对积分区域 $D$ 做如图 2 所示的切分移位之后，可以算出：

$$\iint 1dxdy=1\times (\frac{\pi }{2}+\frac{\pi }{2})=\pi .$$

P.S: $\iint 1dxdy$ 中的 $1$ 表示的是 $z=1$, 并且，在三维直角坐标系中，$z=1$ 位于 $z$ 轴的正半轴，因此，$\iint 1dxdy$ 所表示的曲顶柱体的有向体积一定是个正数。

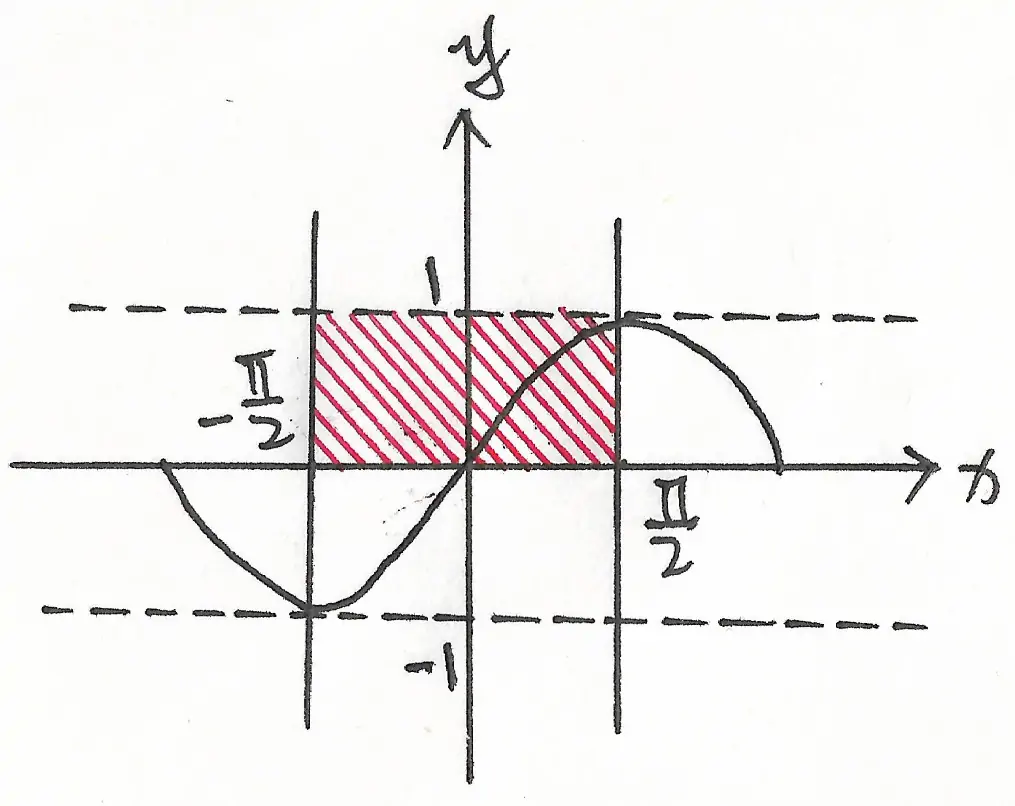
于是有：

$${\iint }_D(x{y}^5)dxdy–\pi =$$

$${\int }_{-\frac{\pi }{2}}^{\frac{\pi }{2}}xdx{\int }_{\sin x}^1{y}^{5}dy–\pi =$$

$${\int }_{-\frac{\pi }{2}}^{\frac{\pi }{2}}[\frac{1}{6}x–\frac{1}{6}x(\sin x{)}^6]dx–\pi =$$

$$\frac{1}{6}{\int }_{-\frac{\pi }{2}}^{\frac{\pi }{2}}xdx–\frac{1}{6}{\int }_{-\frac{\pi }{2}}^{\frac{\pi }{2}}x(\sin x{)}^{6}dx–\pi \Rightarrow$$

由于 $[-\frac{\pi }{2},\frac{\pi }{2}]$ 关于原点对称，且 $y=x$ 与 $y=x(\sin x{)}^6$ 均是关于 $x$ 的奇函数，因此：

$${\int }_{-\frac{\pi }{2}}^{\frac{\pi }{2}}xdx=0;$$

$${\int }_{-\frac{\pi }{2}}^{\frac{\pi }{2}}x(\sin x{)}^{6}dx=0.$$

于是：

$$\mathrm{原}\mathrm{式}=0–0–\pi =–\pi .$$

方法二

计算二重积分一般可以考虑利用积分区间的对称性，虽然本题中给出的积分区域不是对称的，但是，经过切分之后可以变成对称的，如图 3 所示：

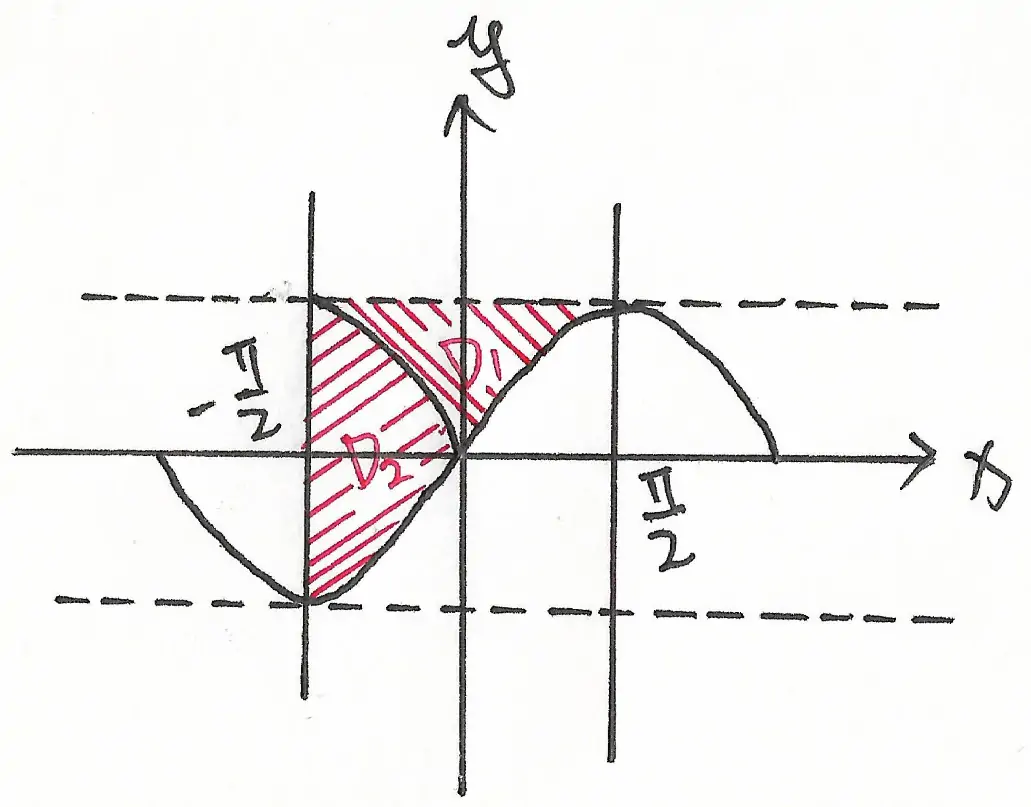
于是：

$${\iint }_D(x{y}^5–1)dxdy=$$

$${\iint }_{D_1}(x{y}^5–1)dxdy+{\iint }_{D_2}(x{y}^5–1)dxdy=$$

$${\iint }_{D_1}(x{y}^5)dxdy–{\iint }_{D_1}1dxdy+$$

$${\iint }_{D_2}(x{y}^5)dxdy–{\iint }_{D_2}1dxdy=$$

由于 $x{y}^5$ 既是关于 $x$ 的奇函数也是关于 $y$ 的奇函数，而且积分区域 $D_1$ 关于 $y$ 轴对称，积分区域 $D_2$ 关于 $x$ 轴对称，所以：

$${\iint }_{D_1}(x{y}^5)dxdy=0;$$

$${\iint }_{D_2}(x{y}^5)dxdy=0.$$

于是有：

$$0–{\iint }_{D_1}1dxdy+0–{\iint }_{D_2}1dxdy=$$

$$-{\iint }_{D}1dxdy=$$

$$-{\int }_{\frac{\pi }{2}}^{-\frac{\pi }{2}}1dx{\int }_{\sin x}^{1}1dy=$$

$$-{\int }_{\frac{\pi }{2}}^{-\frac{\pi }{2}}(1–\sin x)dx=$$

$$-(x+\cos x){|}_{-\frac{\pi }{2}}^{\frac{\pi }{2}}=$$

$$-(\frac{\pi }{2}+0+\frac{\pi }{2}–0)=$$

$$-\pi .$$

注意：在方法二中也可以使用方法一中对积分区域 $D$ 切分移位的方法算出 ${\iint }_{D}1dxdy$ 的数值，进而得出 $-{\iint }_{D}1dxdy$ 的数值。

综上可知，正确选项为 $D$.

EOF