[高数]如何理解变限积分的几何含义

如果我们把定积分看成“静止”的，那么变限积分就是“运动”的——

定积分表示的是【被积函数在积分区间内与坐标轴围成的区域的面积的大小】，如图 1 所示：

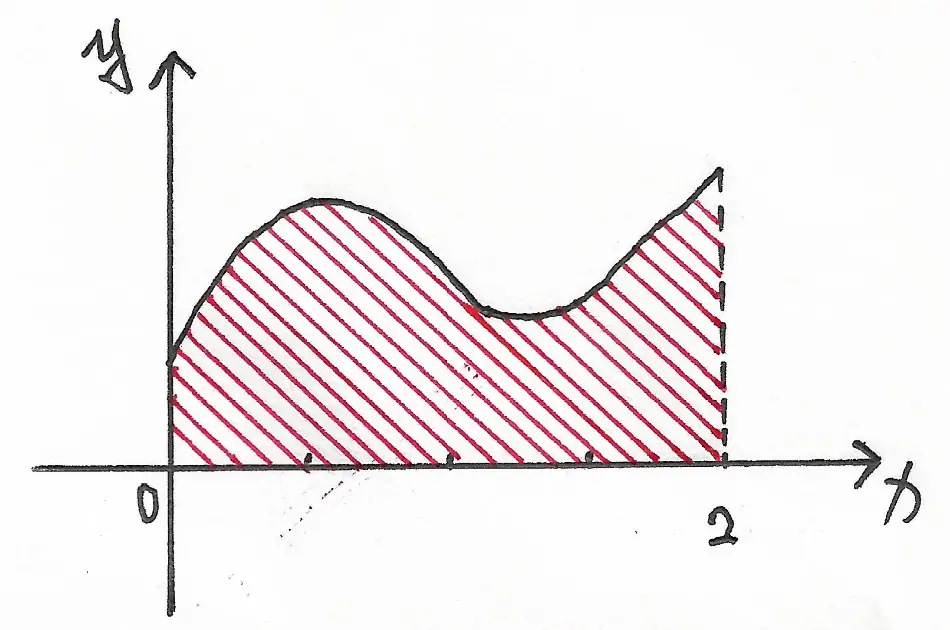
变限积分表示的是【被积函数在积分区间内与坐标轴围成的区域的面积的大小的变化】。如图 2 ~ 4 所示，在积分区间 $[0,x]$ 内，随着 $x$ 的不断变化，变限积分对应于不同的面积：

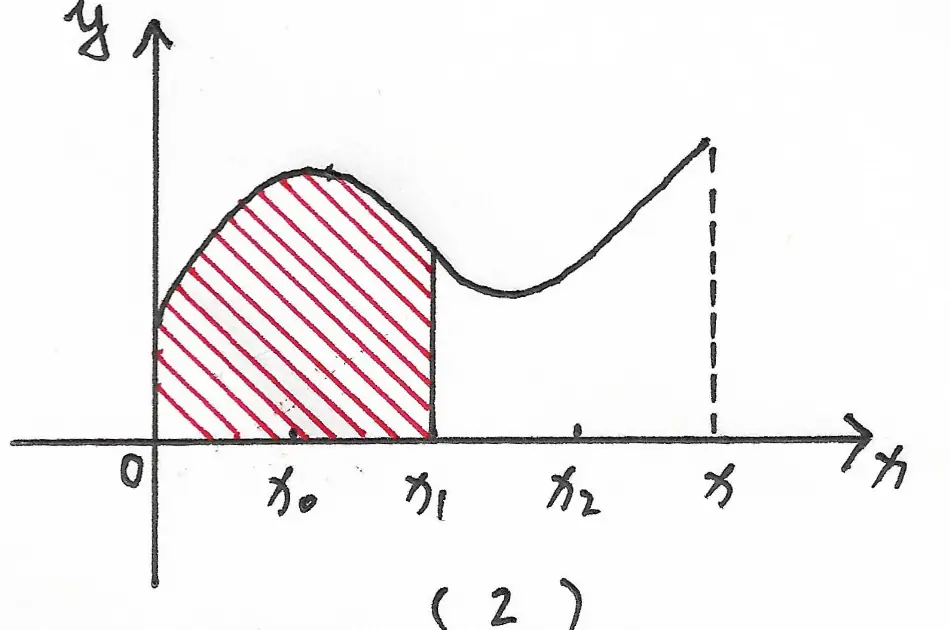
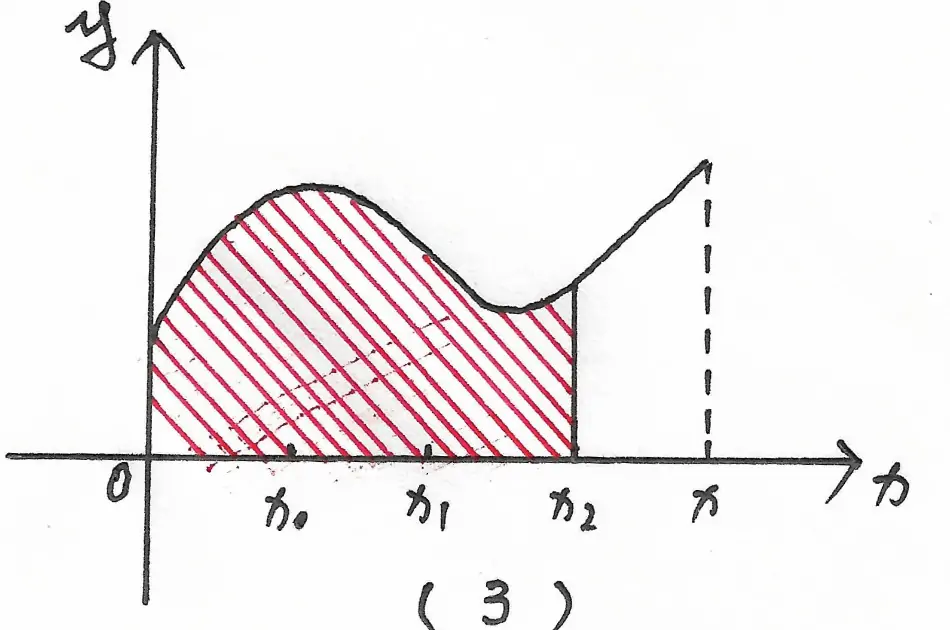
另一方面来看，定积分的计算结果是一个描述积分面积大小的【数值】，而变限积分的计算结果则是一个描述积分面积随 $x$ 的变化而变化的【曲线】。

在具体计算变现积分的时候，我们只需要把其上限或者下限中的未知量【看作】是一个【常数】即可，此时，变限积分与定积分在计算和性质上基本没有差别，可以把变限积分当作定积分进行计算。

EOF