题目
$\int_{-1}^{0} dx \int_{-x}^{2-x^{2}} (1-xy) dy +\int_{0}^{1} dx \int_{x}^{2-x^{2}} (1-xy) dy=?$
$$A. \frac{5}{3}$$
$$B. \frac{5}{6}$$
$$C. \frac{7}{3}$$
$$D. \frac{7}{6}$$
解析
方法一
本方法就是直接算，先对 $y$ 求积分，再对 $x$ 求积分。
由于直接计算过程较繁琐，因此，计算过程中要格外仔细，最好每一步都回头检查一下。
由于：
$$
\int_{-x}^{2-x^{2}} (1-xy) dy =
$$
$$
y-\frac{1}{2} y^{2}x|_{-x}^{2-x^{2}} =
$$
$$
[2-x^{2} – \frac{1}{2} (2-x^{2})^{2} x]-[-x-\frac{1}{2}(-x)^{2}x]=
$$
$$
[2-x^{2} – \frac{1}{2}x(4+x^{4}-4x^{2})]-[-x-\frac{1}{2}x^{3}] =
$$
$$
2-x^{2} – 2x – \frac{1}{2}x^{5} + 2x^{3} + x + \frac{1}{2}x^{3} =
$$
$$
2-x^{2}-x + \frac{5}{2}x^{3}-\frac{1}{2}x^{5}.
$$
于是：
$$
\int_{-1}^{0} dx \int_{-x}^{2-x^{2}} (1-xy) dy =
$$
$$
\int_{-1}^{0} (2-x^{2}-x + \frac{5}{2}x^{3}-\frac{1}{2}x^{5}) dx =
$$
$$
2x – \frac{1}{3}x^{3} – \frac{1}{2}x^{2} + \frac{5}{2} \cdot \frac{1}{4}x^{4} – \frac{1}{2} \cdot \frac{1}{6} x^{6}|_{-1}^{0} =
$$
$$
[0]-[-2 + \frac{1}{3} -\frac{1}{2} + \frac{5}{8} – \frac{1}{12}] =
$$
$$
2 – \frac{1}{3} + \frac{1}{2} – \frac{5}{8} + \frac{1}{12} = \frac{13}{8}.
$$
又由于：
$$
\int_{x}^{2-x^{2}} (1-xy) dy =
$$
$$
y-\frac{1}{2}y^{2}x|_{x}^{2-x^{2}} =
$$
$$
[2-x^{2} – \frac{1}{2}x(2-x^{2})^{2}]-[x – \frac{1}{2}x^{3}] =
$$
$$
[2-x^{2}-\frac{1}{2}x(4+x^{4}-4x^{2})] – x + \frac{1}{2}x^{3} =
$$
$$
2 – x^{2} – 2x – \frac{1}{2} x^{5} + 2x^{3} – x + \frac{1}{2}x^{3} =
$$
$$
2-x^{2}-3x+\frac{5}{2}x^{3}-\frac{1}{2}x^{5} =
$$
于是：
$$
\int_{0}^{1} dx \int_{x}^{2-x^{2}} (1-xy) dy=
$$
$$
\int_{0}^{1} 2-x^{2}-3x+\frac{5}{2}x^{3}-\frac{1}{2}x^{5} dx =
$$
$$
2x – \frac{1}{3}x^{3} – 3 \cdot \frac{1}{2} x^{2} + \frac{5}{2} \cdot \frac{1}{4}x^{4} – \frac{1}{2} \cdot \frac{1}{6} x^{6} |_{0}^{1} =
$$
$$
[2-\frac{1}{3} – \frac{3}{2} + \frac{5}{8} – \frac{1}{12}] – [0] = \frac{17}{24}
$$
所以：
$$
原式 = \frac{13}{8} + \frac{17}{24} = \frac{7}{3}.
$$
综上可知，正确选项为 $C$.
方法二
本题也可以通过一些化简之后再进行计算。
本题是计算二重积分，而且式子中 $”+”$ 号两侧的被积函数都是相同的，因此，可以尝试画出积分区域 $D$, 看是否可以化简。
由题可知，积分区域 $D=$:
$$
\{ (x, y) | -1 \leqslant x \leqslant 0, -x \leqslant y \leqslant 2-x^{2} \}
$$
$$
\cup \{ (x, y) | 0 \leqslant x \leqslant 1, x \leqslant y \leqslant 2-x^{2} \}
$$
画出图形就是 (图 1)：
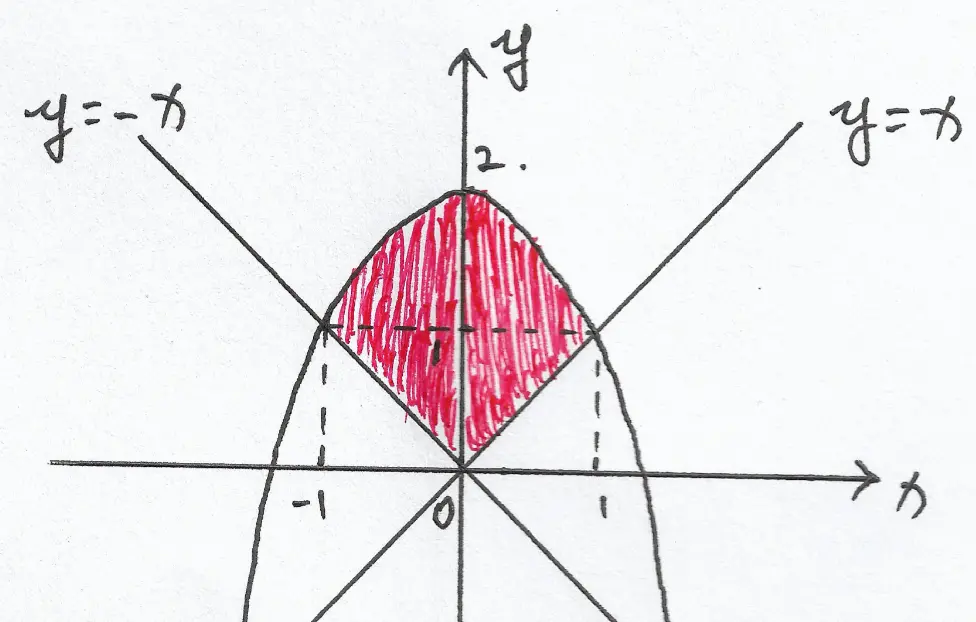
由图可知，积分区域 $D$ 关于 $y$ 轴对称。又因为，在 $1-xy$ 中，$xy$ 关于 $x$ 为奇函数，$1$ 关于 $x$ 为偶函数，于是：
$$
\int_{-1}^{0} dx \int_{-x}^{2-x^{2}} (1-xy) dy +\int_{0}^{1} dx \int_{x}^{2-x^{2}} (1-xy) dy=
$$
$$
\iint_{D} (1-xy) dxdy=
$$
$$
\iint_{D} 1 dxdy – \iint_{D} xy dxdy =
$$
$$
\iint_{D} 1 dxdy – 0 =
$$
$$
2 \int_{0}^{1} dx \int_{x}^{2-x^{2}} 1 dy =
$$
$$
2 \int_{0}^{1} (2-x^{2}-x)dx =
$$
$$
2 \cdot (2x – \frac{1}{3}x^{3} – \frac{1}{2}x^{2}) |_{0}^{1} =
$$
$$
2 \cdot (2 – \frac{1}{3} – \frac{1}{2} – 0)=
$$
$$
2 \cdot \frac{7}{6} = \frac{7}{3}.
$$
综上可知，正确选项为 $C$.
EOF