考研数学 – 第 167 页

题目

编号：A2016203

反常积分 $① \int_{- \infty}^{0} \frac{1}{x^{2}} e^{\frac{1}{x}} dx$, $② \int_{0}^{+ \infty} \frac{1}{x^{2}} e^{\frac{1}{x}} dx$ 的敛散性为 $?$

$$A. ① 收敛，② 收敛$$

$$B. ① 收敛，② 发散$$

$$C. ① 发散，② 收敛$$

$$D. ① 发散，② 发散$$

继续阅读

题目

编号：A2016202

已知函数 $f(x)=\left\{\begin{matrix}2(x-1),x < 1,\\ \ln x, x \geqslant 1,\end{matrix}\right.$ 则 $f(x)$ 的一个原函数是 $?$

$$
A. F(x)=\left\{\begin{matrix}(x-1)^{2},x < 1,\\ x(\ln x – 1), x \geqslant 1,\end{matrix}\right.$$

$$B. F(x)=\left\{\begin{matrix}(x-1)^{2},x < 1,\\ x(\ln x + 1) – 1, x \geqslant 1,\end{matrix}\right.$$

$$C. F(x)=\left\{\begin{matrix}(x-1)^{2},x < 1,\\ x(\ln x + 1) + 1, x \geqslant 1,\end{matrix}\right.$$

$$D. F(x)=\left\{\begin{matrix}(x-1)^{2},x < 1,\\ x(\ln x – 1) + 1, x \geqslant 1,\end{matrix}\right.$$

继续阅读

题目

编号：A2016201

设 $\alpha_{1} = x(\cos \sqrt{x}-1)$, $\alpha_{2} = \sqrt{x}\ln(1+\sqrt[3]{x})$, $\alpha_{3} = \sqrt[3]{x+1}-1$.

当 $x \rightarrow 0^{+}$ 时，以上 $3$ 个无穷小量按照从低阶到高阶的排序是 $?$

$$A. \alpha_{1}, \alpha_{2}, \alpha_{3}$$

$$B. \alpha_{2}, \alpha_{3}, \alpha_{1}$$

$$C. \alpha_{2}, \alpha_{1}, \alpha_{3}$$

$$D. \alpha_{3}, \alpha_{2}, \alpha_{1}$$

继续阅读

一、题目

设矩阵 $A=\begin{bmatrix}
4 & 1 & -2 \\
1 & 2 & a \\
3 & 1 & -1
\end{bmatrix}$ 的一个特征向量为 $\begin{bmatrix}
1 \\
1 \\
2
\end{bmatrix}$, 则 $a=?$

继续阅读

一、题目

$$
\int_{0}^{1} dy \int_{y}^{1} \frac{\tan x}{x} \mathrm{~d} x = ?
$$

继续阅读

一、题目

设函数 $f(x,y)$ 具有一阶连续偏导数，且 $\mathrm{d} f(x,y) =y \mathrm{e}^{y} \mathrm{d} x + x(1+y) \mathrm{e}^{y} \mathrm{d} y$, $f(0,0)=0$, 则 $f(x,y)=?$

继续阅读

一、题目

$$
\int_{0}^{+ \infty} \frac{\ln (1+x)}{(1+x)^{2}} \mathrm{~d} x = ?
$$

继续阅读

一、题目

设函数 $y=y(x)$ 由参数方程 $\left\{\begin{matrix}
x = t + \mathrm{e}^{t},\\
y = \sin t
\end{matrix}\right.$ 确定，则 $\frac{\mathrm{d}^{2}y}{\mathrm{d} x^{2}}|_{t=0}$ = $?$

继续阅读

一、题目

曲线 $y=x(1 + \arcsin \frac{2}{x})$ 的斜渐近线方程为 $?$

继续阅读

一、题目

已知矩阵 $\boldsymbol{A}$ $=$ $\begin{bmatrix}
2 & 0 & 0 \\
0 & 2 & 1 \\
0 & 0 & 1
\end{bmatrix}$, $\boldsymbol{B}$ $=$ $\begin{bmatrix}
2 & 1 & 0 \\
0 & 2 & 0 \\
0 & 0 & 1
\end{bmatrix}$, $\boldsymbol{C}$ $=$ $\begin{bmatrix}
1 & 0 & 0 \\
0 & 2 & 0 \\
0 & 0 & 2
\end{bmatrix}$, 则 $?$

A. $\boldsymbol{A}$ 与 $\boldsymbol{C}$ 相似，$\boldsymbol{B}$ 与 $\boldsymbol{C}$ 相似

B. $\boldsymbol{A}$ 与 $\boldsymbol{C}$ 相似，$\boldsymbol{B}$ 与 $\boldsymbol{C}$ 不相似

C. $\boldsymbol{A}$ 与 $\boldsymbol{C}$ 不相似，$\boldsymbol{B}$ 与 $\boldsymbol{C}$ 相似

D. $\boldsymbol{A}$ 与 $\boldsymbol{C}$ 不相似，$\boldsymbol{B}$ 与 $\boldsymbol{C}$ 不相似

继续阅读

如何判断 i 重特征值对应的线性无关的特征向量的个数

判断 $i$ 重特征值对应的线性无关的特征向量的个数有具体的公式。例如，当 $\lambda_{a}$ 为 $i$ 重特征值时，则 $\lambda_{a} E – A$ 的秩，即 $r(\lambda_{a} E – A)$ 就是 $\lambda_{a}$ 对应的线性无关的特征向量的个数。

下面是我对 $r(\lambda_{a} E – A)$ 之所以能够表示 $\lambda_{a}$ 对应的线性无关的向量的个数的原理的理解。

下面的理解可能不够严谨，做出这样的理解只是为了方便记忆公式，仅供参考。

继续阅读

2017年考研数二第07题解析：可逆矩阵、相似对角化

一、题目

设 $A$ 为 $3$ 阶矩阵，$P$ $=$ $(\alpha_{1}, \alpha_{2}, \alpha_{3})$ 为可逆矩阵，使得 $P^{-1}AP$ $=$ $\begin{bmatrix}
0& 0& 0\\
0& 1& 0\\
0& 0& 2
\end{bmatrix}$, 则 $A(\alpha_{1}$ $+$ $\alpha_{2}$ $+$ $\alpha_{3})$ $=$ $?$

⟨A⟩. $\alpha_{1} + \alpha_{2}$

⟨C⟩. $\alpha_{2} + \alpha_{3}$

⟨B⟩. $\alpha_{2} + 2 \alpha_{3}$

⟨D⟩. $\alpha_{1} + 2 \alpha_{2}$

继续阅读

2017年考研数二第06题解析：工程应用

一、题目

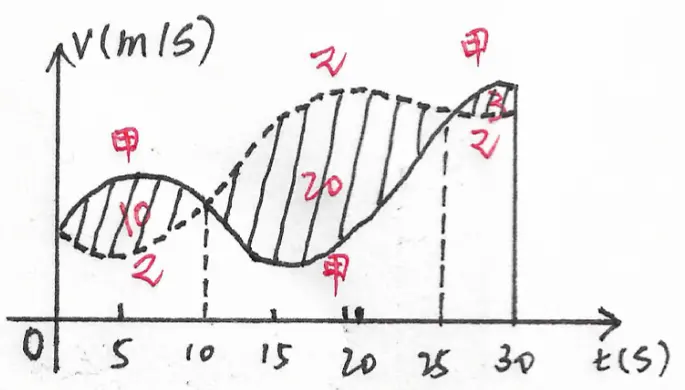
甲乙两人赛跑，计时开始时，甲在乙前方 $10$（单位：$m$）处. 图 1 中，实线表示甲的速度曲线 $v=v_{1}(t)$ （单位 : m/s），虚线表示乙的速度曲线 $v=v_{2}(t)$ （单位 : m/s），三块阴影部分面积的数值依次为 $10$, $20$, $3$. 计时开始后乙追上甲的时刻记为 $t_{0}$ （单位 : $s$），则 $?$

⟨A⟩. $t_{0}=10$.

⟨C⟩. $t_{0}=25$.

⟨B⟩. $15<t_{0}<20$.

⟨D⟩. $t_{0}>25$.