作者: 荒原之梦
[高数]一些初等函数的函数图像(精确矢量图)
前言
在有些题目中,特别是在选择题中,使用画图的方式辅助解题有时可以减少很多计算步骤。但是,使用画图方式解题的一个重要前提就是画的图在关键节点上是相对准确的。为此,本文将提供一些初等函数的函数图像,全部都是较为精确的矢量图,以作参考。
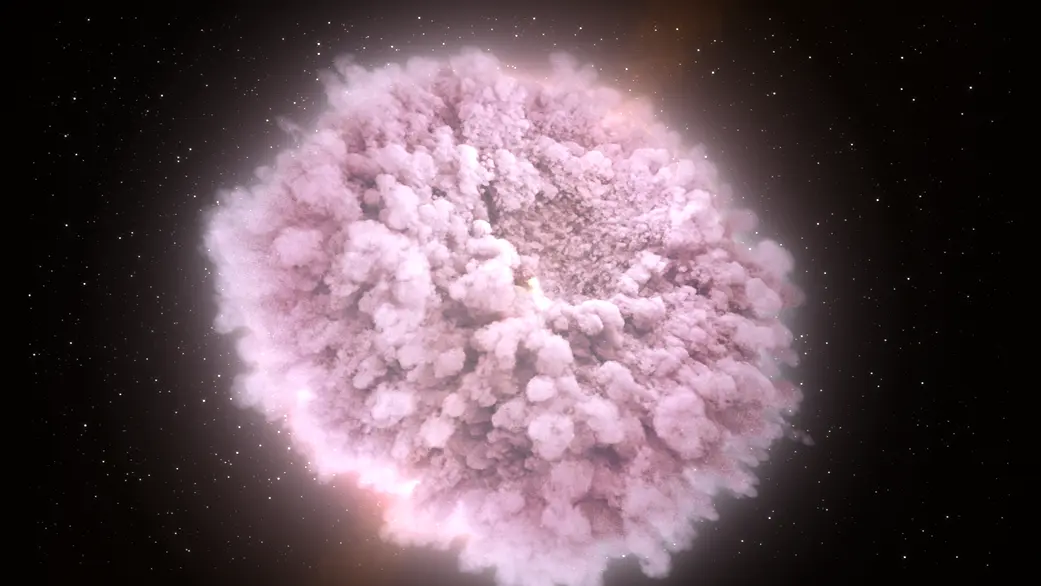
继续阅读“[高数]一些初等函数的函数图像(精确矢量图)”苏醒的中子星会创造大量的黄金和铂金
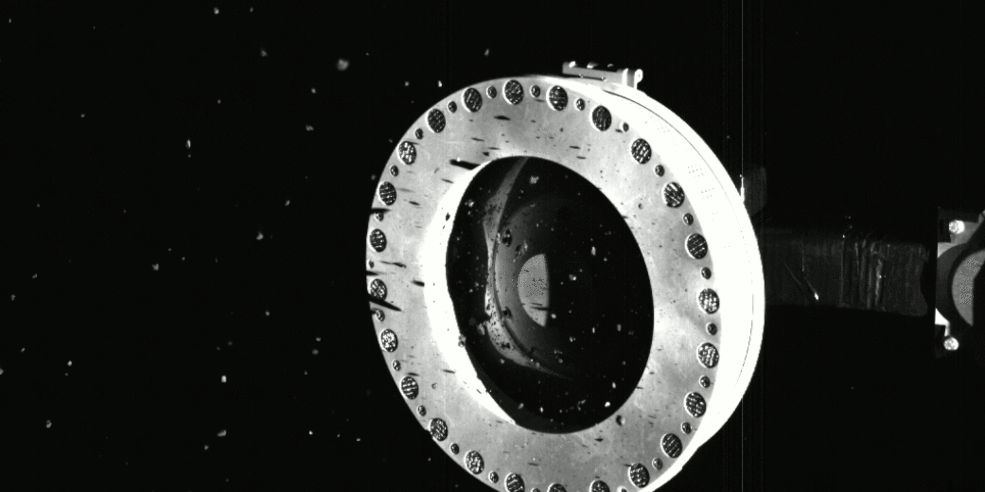
美国宇航局OSIRIS-REx探测器已经从小行星贝努表面收集到了足够的样本
美国宇航局OSIRIS-REx探测器在小行星贝努表面成功完成采样
[数据结构基础]使用顺序存储方式存储多维数组时特定元素存储地址的计算方法
前言
本文将分析并给出将一维数组、二维数组和三维数组使用顺序存储方式存储时确定给定的某个数组元素在内存中的存储地址的计算方法,以作参考。
继续阅读“[数据结构基础]使用顺序存储方式存储多维数组时特定元素存储地址的计算方法”俄罗斯苏-30SM、米格-31和苏-35战机战术演习图集
该图集来自俄罗斯国防部英文官网 (eng.mil.ru), 展示了俄罗斯部署在列宁格勒的空军和防空军在阿斯特拉罕和沃罗涅日地区举行的一次由苏 – 30 SM、米格 – 31 和苏 – 35 三款战机参与的战术飞行演习的最后阶段。
继续阅读“俄罗斯苏-30SM、米格-31和苏-35战机战术演习图集”从太空中俯瞰夏威夷岛链
毅力号火星车拍摄的地球和金星同框照
[高数]有界震荡无极限与无界震荡无极限
前言
和《[高数]形象化理解无穷大量与无界函数之间的关系》中所分析的“何为无穷”类似,【极限】也是“过程”的产物,而且这个过程必须是无间断的,单调的过程。于是,所有间断点都是极限不存在的点——震荡间断点自然也是极限不存在的点。
如果细分的话,震荡间断点又可以分为“有界震荡无极限”和“无界震荡无极限”两类间断点,本文将对此分别给出两个实际函数的图像,以作参考。
继续阅读“[高数]有界震荡无极限与无界震荡无极限”火星地表下或许存在大量的冰层
[高数]形象化理解无穷大量与无界函数之间的关系
前言
关于【无穷大】与【无界】的关系,可以通过严格的数学语言加以证明。但是,出于更易于理解的目的,本文将通过两个具体的函数图像来形象化地展示这两者之间的关系。
继续阅读“[高数]形象化理解无穷大量与无界函数之间的关系”正在起飞的KC-135加油机
[高数]洛必达法则的适用条件
前言
在解题时,有时需要使用一次或者多次洛必达法则,但是,要特别注意的是,在每一次使用洛必达法则时都要想一想和检查一下使用洛必达法则的条件是否满足,以免发生错误。
继续阅读“[高数]洛必达法则的适用条件”