题目
编号:A2016204
设函数 $f(x)$ 在 $(- \infty, + \infty)$ 内连续,其导函数的图形如图1 所示,则 $?$
$$
A. 函数 f(x) 有 2 个极值点,曲线 y=f(x) 有 2 个拐点
$$
$$
B. 函数 f(x) 有 2 个极值点,曲线 y=f(x) 有 3 个拐点
$$
$$
C. 函数 f(x) 有 3 个极值点,曲线 y=f(x) 有 1 个拐点
$$
$$
D. 函数 f(x) 有 3 个极值点,曲线 y=f(x) 有 2 个拐点
$$
解析
本题考查的就是极值点和拐点的知识。
- 极值点
$f(x)$ 增减性发生改变的点 $\Leftrightarrow$ $f^{‘}(x)$ 的正负发生改变的点。
注意:虽然,若 $(t,f^{‘}(t))$ 为极值点时,有 $f^{‘}(t) = 0$, 但仅凭 $f^{‘}(r) = 0$ 是无法确定 $(r, f^{‘}(r))$ 是极值点的。因为,极值点的本质是一阶导的正负发生改变的点,极值点处的一阶导为零只是这一前提的必然结果而已。反之,一阶导为零的点并不一定是一阶导的正负发生改变的点。
- 拐点
$f(x)$ 的凹凸性发生改变的点 $\Leftrightarrow$ $f^{‘}(x)$ 的增减性发生改变的点 $\Leftrightarrow$ $f^{”}(x)$ 的正负发生改变的点。
注意:同上述在【极值点】处的分析,$f^{”}(x)=0$ 对应的点并不一定是拐点。
据此,解题过程如图 1 所示:
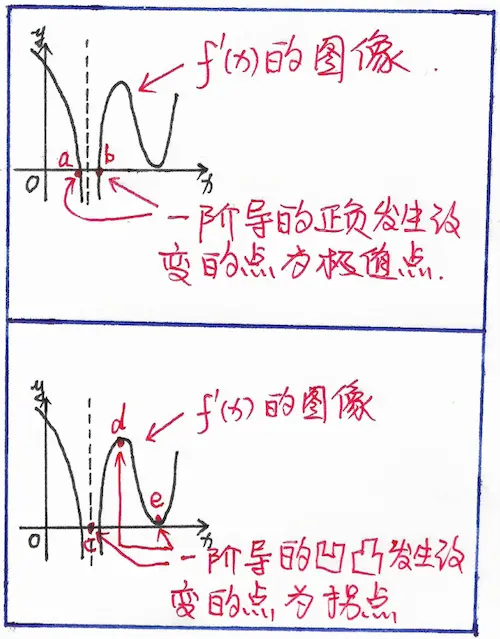
由上可知,$f(x)$ 的极值点有 $a,b$ 两个,$y=f(x)$ 的拐点有 $c,d,e$ 三个。
本题中容易忽略的一个拐点就是 $c$ 点。由于题目中说明了 $f(x)$ 在 $(- \infty, + \infty)$ 上连续,那么 $f(x)$ 在 $c$ 点一定是有定义的,又因为在 $c$ 点两侧,$f^{‘}(x)$ 的凹凸性发生了改变,于是,$c$ 点一定是拐点之一。
——这毕竟是考研试题,至少要有一点弯儿的,很少有题会直接用概念就能解出而不需要思考一下。
本题另外一个需要注意的地方是,题中给出的图像时 $f^{‘}(x)$ 的图像,而不是 $f(x)$ 的图像。
——仔细读题。
综上可知,正确答案为 $B$.
EOF