一、充分条件
若由 $A$ 能够推导出 $B$, 但是由 $B$ 不能够推导出 $A$, 则称 $A$ 是 $B$ 的充分不必要条件($B$ 的充分不必要条件是 $A$.)。
从集合的角度看,就是 $A \in B$, 如图 1:
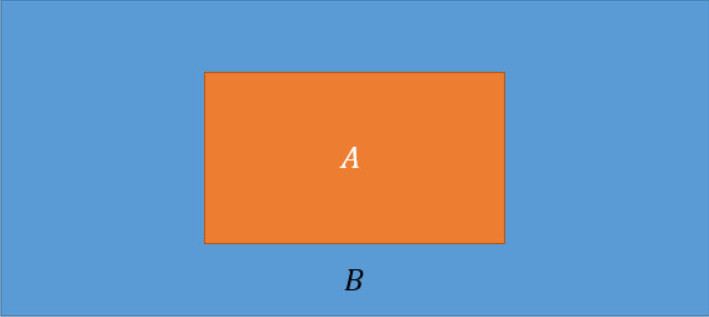
二、必要条件
若由 $A$ 不能推导出 $B$, 但是由 $B$ 可以推导出 $A$, 则称 $A$ 是 $B$ 的必要不充分条件($B$ 的必要不充分条件是 $A$.)。
从集合的角度看,就是 $B \in A$, 如图 2:
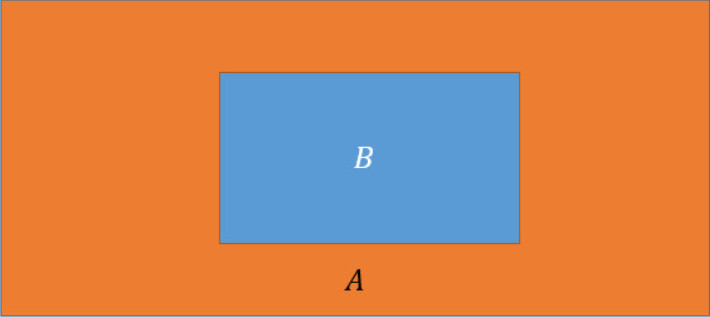
三、充要条件
若由 $A$ 可以推导出 $B$, 而且由 $B$ 也可以推导出 $A$, 则称 $A$ 是 $B$ 的充分必要条件($B$ 的充分必要条件是 $A$.)。
从集合的角度看,就是 $A=B$, 如图 3:

“充要条件”是“充分必要条件”的简化称呼,和“充要条件”等价的表述还有“当且仅当”,“唯一条件”和“需要且仅需要”等表述,他们之间的关系如下所示:
充分必要条件 $\Leftrightarrow$ 充要条件 $\Leftrightarrow$ 唯一条件 $\Leftrightarrow$ 当且仅当 $\Leftrightarrow$ 需要且仅需要.
四、总览
五、总结
“必要条件”指代的范围较大,“充分条件”指代的范围较小。为了方便记忆,我们可以使用下面这个顺口溜:
小充分,大必要。
高等数学
涵盖高等数学基础概念、解题技巧等内容,图文并茂,计算过程清晰严谨。
线性代数
以独特的视角解析线性代数,让繁复的知识变得直观明了。
特别专题
通过专题的形式对数学知识结构做必要的补充,使所学知识更加连贯坚实。
EOF