题目
设 $D_{k}$ 是圆域 $D={(x,y) | x^{2} + y^{2} \leqslant 1 }$ 在第 $k$ 象限的部分,记 $I_{k}=\iint_{D_{k}} (y-x) dxdy (k=1,2,3,4)$, 则 $?$
$$
A. I_{1} > 0
$$
$$
B. I_{2} > 0
$$
$$
C. I_{3} > 0
$$
$$
D. I_{4} > 0
$$
解析
对于二重积分,首先要画出积分区域,本题中的积分区域如图 1 所示:
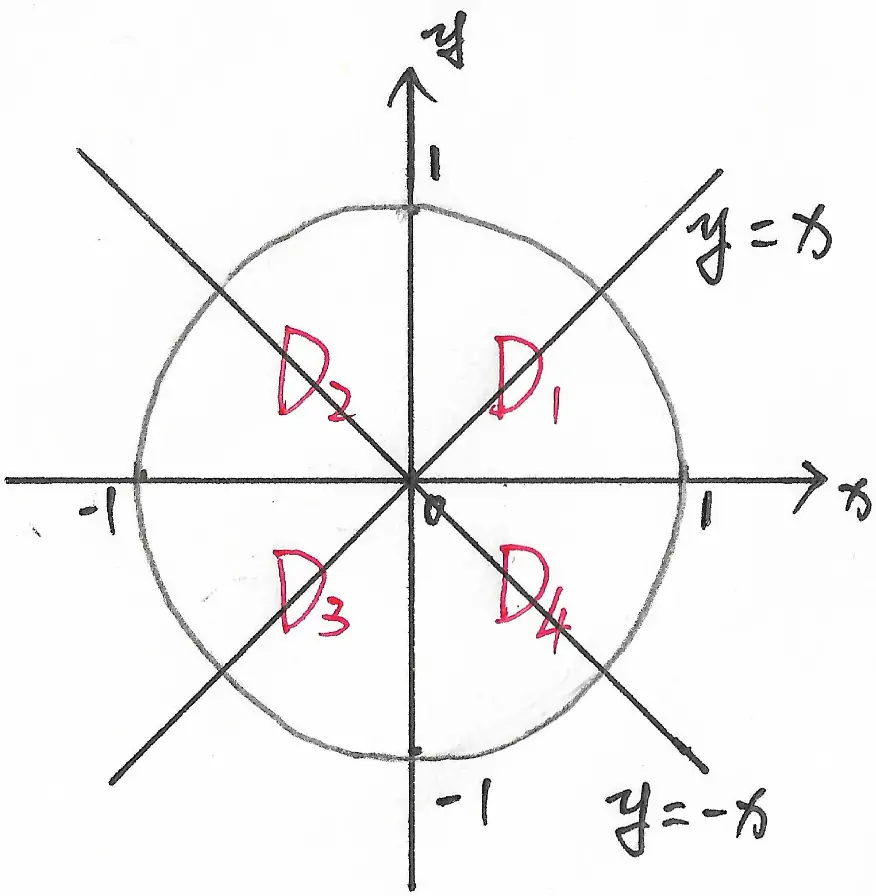
由于这个积分区域 $D$ 具有很强的对称性,因此,我们首先考虑能否利用对称性做一些判断。
由图知,$D_{1}$ 和 $D_{3}$ 关于直线 $y=x$ 对称,因此:
$$
\iint_{D_{1,3}} (y-x) dxdy =
$$
$$
\iint_{D_{1,3}} (x-y)dxdy =
$$
$$
\frac{1}{2} \iint_{D_{1,3}} [(y-x) + (x-y)] dxdy = 0.
$$
因此:
$$
I_{1} = I_{3} = 0.
$$
于是,可以排除 $A$, $C$ 两个选项。
又由图知,$D_{2}$ 和 $D_{4}$ 关于直线 $y=-x$ 对称,因此:
$$
\iint_{D_{2,4}} (y-x) dxdy =
$$
$$
\iint_{D_{2,4}} [y + (-x)] dxdy
$$
又因为,在第二象限内,$x<0,y>0$, 于是 $y+(-x) > 0$, 因此:
$$
I_{2} = \iint_{D_{2}} [y + (-x)] > 0.
$$
而在第四象限内,$x>0,y<0$, 于是 $y+(-x)<0$, 因此:
$$
I_{4} = \iint_{D_{4}} [y + (-x)] < 0.
$$
补充:
综上可知,正确选项为 $B$.
EOF