2017年考研数二第13题解析：改变二重积分的积分次序

一、题目

二、解析

对于一重积分，我们只能从被积函数（根据被积函数找原函数）以及积分上下限（当积分上下限关于 $x$ 轴或者 $y$ 轴对称的时候，考虑是否能化简，是否能利用奇偶函数的性质等）。但对于二重积分，我们除了可以使用上述用于一重积分的思考方法之外，还可以从积分次序上寻找突破口——对于二重积分，如果不知道怎么算，就先尝试画出积分区域。

对于本题，被积函数 $\frac{\tan x}{x}$ 如果先对 $x$ 求积分的话，很难找到求原函数（既没有相应的积分公式，也没有可用的积分技巧），因此，这里先画出积分区域，看一看是否可以通过改变积分次序找到突破口，如图 1:

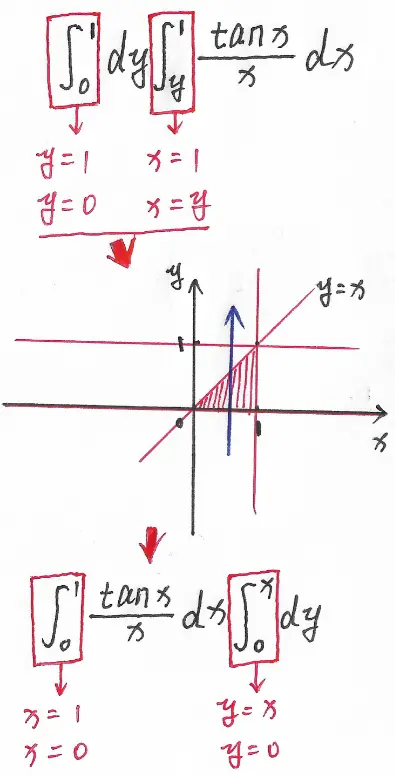
图 1

于是，我们有：

$$
\int_{0}^{1} \mathrm{~d} y \int_{y}^{1} \frac{\tan x}{x} \mathrm{~d} x =
$$

$$
\int_{0}^{1} \frac{\tan x}{x} \mathrm{~d} x \int_{0}^{x} 1 \mathrm{~d} y =
$$

$$
\int_{0}^{1} \frac{\tan x}{x} x \mathrm{~d} x =
$$

$$
\int_{0}^{1} \tan x \mathrm{~d} x =
$$

$$
(-1) \ln |\cos x| \Big|_{0}^{1} =
$$

$$
(-1) \left[\ln \cos 1 – \ln \cos 0 \right] =
$$

其中 $\cos 1 > 0$, $\cos 0 = 1 > 0$.

$$
(-1) \left[\ln \cos 1 – \ln 1 \right]=
$$

$$
(-1) \left[\ln \cos 1 – 0 \right] =
$$

$$
(-1) \ln \cos 1 = – \ln \cos 1
$$

综上可知，正确答案为 $- \ln \cos 1$.

EOF

---