sin(arctan x) 和 cos(arctan x) 怎么算？一张图让你秒懂！

一、前言

你是否被下面两个式子的困惑过：

$$
\sin (\arctan x) = ?
$$

$$
\cos (\arctan x) = ?
$$

在荒原之梦网之前的文章中，曾就这类问题做过详细的推理演算（详情请点击这里），现在，只需要看懂一张图，马上就明白了！

二、解析

首先，有下面这张图：

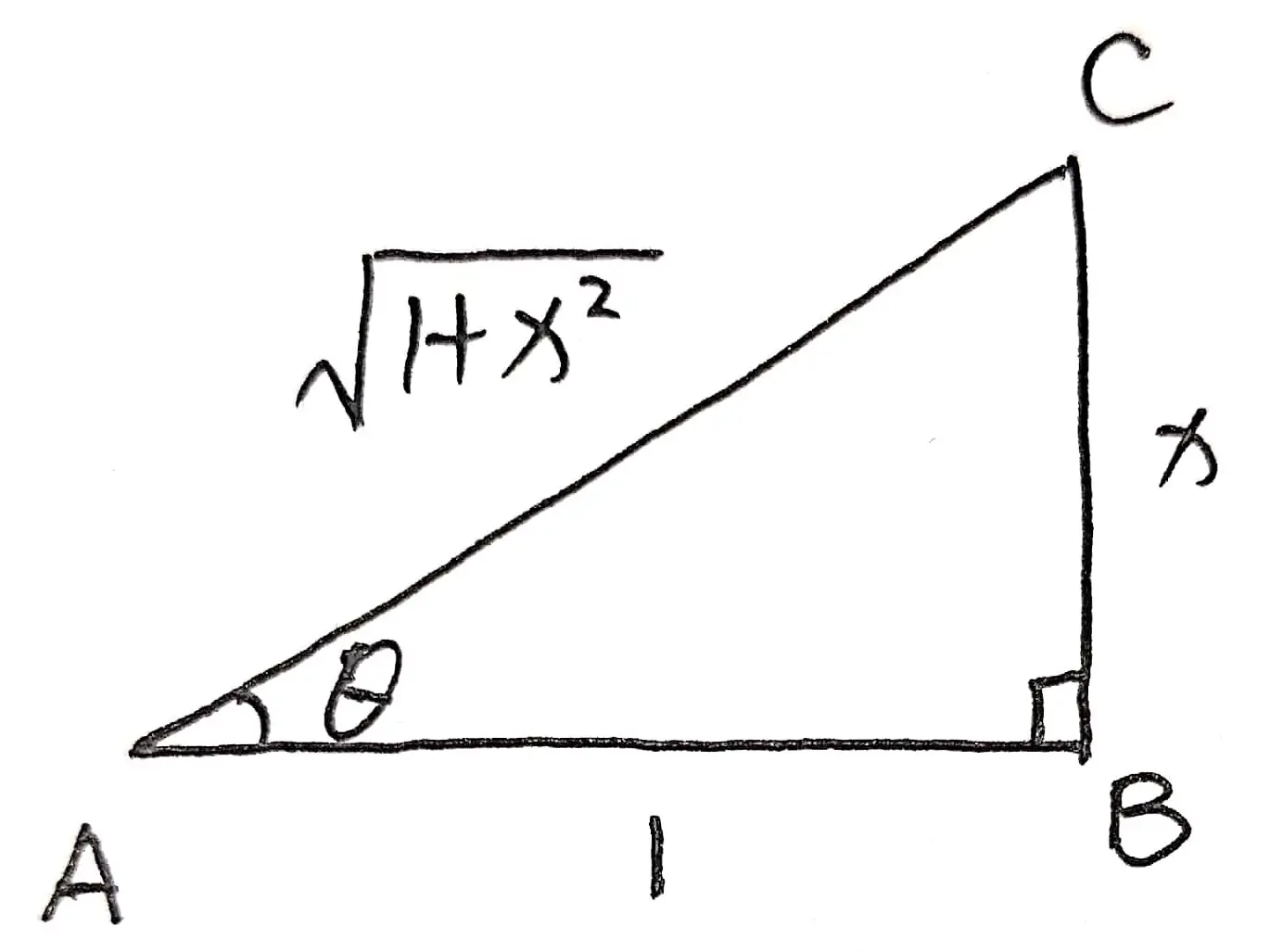
其中，$AB$ 边长为 $1$, $BC$ 边长为 $x$, $\angle ABC = 90^{\circ}$.

于是，根据勾股定理可知，$AC = \sqrt{1+x^2}$

进而，若令 $\arctan x = \theta = \angle BAC$, 则：

$$
\textcolor{orangered}{
\sin (\arctan x) = \frac{x}{\sqrt{1+x^{2}}}
}
$$

$$
\textcolor{springgreen}{
\cos (\arctan x) = \frac{1}{\sqrt{1+x^{2}}}
}
$$

Next

当然，如果是求解 $\sin [\arctan (\frac{x}{2})]$ 和 $\cos [\arctan (\frac{x}{2})]$ 的值，只需要把上面图 01 中的所有 $x$ 都替换为 $\frac{x}{2}$ 即可，于是：

$$
\textcolor{orangered}{
\sin [\arctan (\frac{x}{2})] = \frac{\frac{x}{2}}{\sqrt{1+(\frac{x}{2})^{2}}} = \frac{x}{\sqrt{4+x^{2}}}
}
$$

$$
\textcolor{springgreen}{
\cos [\arctan (\frac{x}{2})] = \frac{1}{\sqrt{1+(\frac{x}{2})^{2}}} = \frac{2}{\sqrt{4+x^{2}}}
}
$$

Next

当然，$\sin [\textcolor{springgreen}{ 2 } \arctan x]$ 和 $\cos [\textcolor{springgreen}{ 2 } \arctan x]$ 的值也可以根据图 01 所示的直角三角形求出来：

根据二倍角公式可知：

$$
\sin [2 \arctan x]=2 \sin [\arctan x] \cos [\arctan x]
$$

$$
\cos [2 \arctan x]=2[\csc (\arctan x)]^{2}-1
$$

又：

$$
\sin \arctan x=\frac{x}{\sqrt{1+x^{2}}}
$$

$$
\cos \arctan x=\frac{1}{\sqrt{1+x^{2}}}
$$

于是：

$$
\textcolor{orangered}{
\sin [2 \arctan x]=\frac{2 x}{1+x^{2}}
}
$$

$$
\textcolor{springgreen}{
\cos [2 \arctan x]=\frac{2-\left(1+x^{2}\right)}{1+x^{2}}=\frac{1-x^{2}}{1+x^{2}}
}
$$

当然也可以得到：

$$
\tan [2 \arctan x]=\frac{2 x}{1+x^{2}} \cdot \frac{1+x^{2}}{1-x^{2}}
$$

$$
\tan [2 \arctan x]=\frac{2 x}{1-x^{2}}
$$

Tips:

如上，若令 $t = \tan \frac{x}{2}$, 就会产生 $x = 2\arctan t$. 这样做三角代换的好处之一就是不会引入根号——$\sin [2 \arctan x]$、$\cos [2 \arctan x]$ 以及 $\tan [2 \arctan x]$ 转变之后，都是没有根号的。

---