题目
过点 $(0,1)$ 作曲线 $L:$ $y = \ln x$ 的切线,切点为 $A$, 又 $L$ 与 $x$ 轴交于 $B$ 点,区域 $D$ 由 $L$ 与直线 $AB$ 围成,求区域 $D$ 的面积及 $D$ 绕 $x$ 轴旋转一周所得旋转体的体积。
解析
根据题目描述,我们可以画出如下示意图,其中,以绿色斜线表示的区域就是区域 $D$:
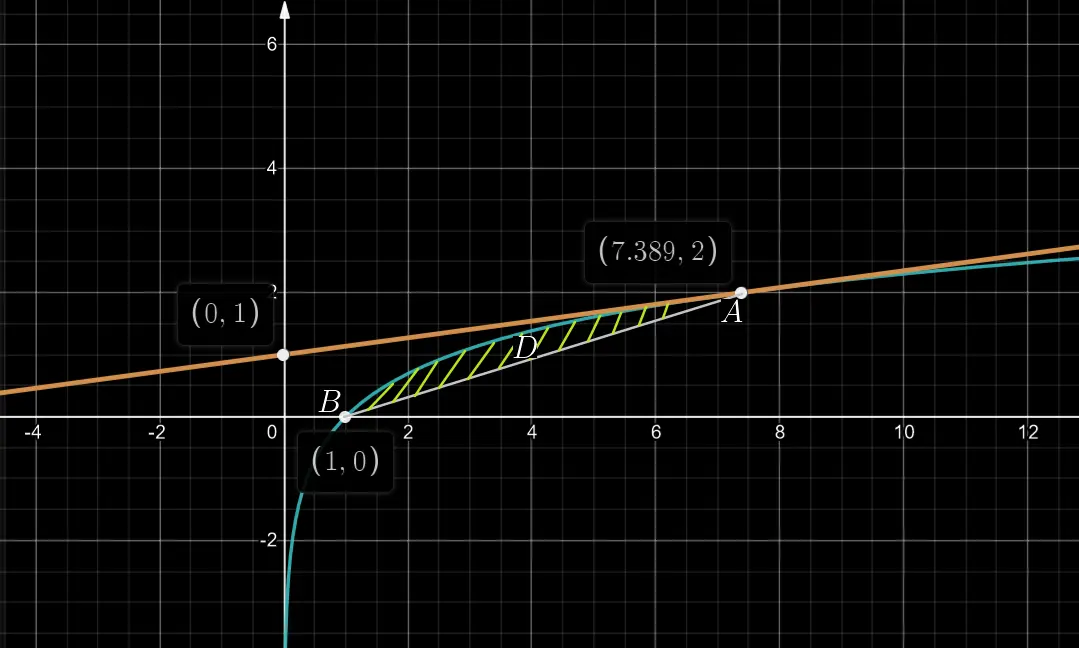
首先,设切线的方程为:
$$
y = kx + b.
$$
将 $(0,1)$ 代入上式,得:
$$
b=1.
$$
于是:
$$
\left\{\begin{matrix}
y = kx + 1;\\
y = \ln x.
\end{matrix}\right.
\Rightarrow
$$
$$
kx + 1 = \ln x \Rightarrow
$$
$$
e^{kx + 1} = e^{\ln x} \Rightarrow
$$
$$
e^{kx + 1} = x.
$$
又:
$$
(\ln x)^{‘} = \frac{1}{x} \Rightarrow
$$
$$
k = \frac{1}{x}.
$$
即:
$$
e^{kx + 1} = x \Rightarrow
$$
$$
x = e^{2}.
$$
把 $x = e^{2}$ 代入到 $y = \ln x$, 得:
$$
y = 2.
$$
即,切线与曲线 $y = \ln x$ 的切点 $A$ 的坐标为:
$$
(e^{2}, 2).
$$
又由题可知,点 $B$ 的坐标为:
$$
(1,0).
$$
于是,区域 $D$ 的面积 $S$ 为:
$$
S = \int_{1}^{e^{2}} \ln x dx – [\frac{1}{2} \cdot 2 \cdot (e^{2} – 1)] \Rightarrow
$$
$$
S = x \cdot \ln x |_{1}^{e^{2}} – \int_{1}^{e^{2}} x d(\ln x) – (e^{2} – 1) \Rightarrow
$$
$$
S = 2e^{2} – \int_{1}^{e^{2}} x \cdot \frac{1}{x} dx – (e^{2} – 1) \Rightarrow
$$
$$
S = 2e^{2} – (e^{2} – 1) – (e^{2} – 1) \Rightarrow
$$
$$
S = e^{2} + 1 – e^{2} + 1 \Rightarrow
$$
$$
S = 2.
$$
区域 $D$ 绕 $x$ 轴旋转一周所得的旋转体的体积 $V$ 为:
$$
V = \pi \int_{1}^{e^{2}} (\ln x)^{2} dx – \frac{1}{3} \pi \cdot 2^{2} \cdot (e^{2}-1) \Rightarrow
$$
注:
圆锥体的体积计算公式为:$V_{圆锥} = \frac{1}{3} \pi R^{2} H$, 其中,$R$ 为圆锥体的底部半径,$H$ 为圆锥体的高度。
$$
V = \pi [\int_{1}^{e^{2}} (\ln x)^{2} dx – \frac{4}{3}(e^{2} – 1)] \Rightarrow
$$
又:
$$
\int_{1}^{e^{2}} (\ln x)^{2} dx =
$$
$$
x (\ln x)^{2} |_{1}^{e^{2}} – \int_{1}^{e^{2}} x d[(\ln x)^{2}] =
$$
$$
4e^{2} – \int_{1}^{e^{2}} x \cdot 2 \ln x \cdot \frac{1}{x} dx =
$$
$$
4e^{2} – 2 \int_{1}^{e^{2}} \ln x dx =
$$
$$
4e^{2} – 2(e^{2} + 1) = 2e^{2} – 2.
$$
于是:
$$
V = \pi [2e^{2} – 2 – \frac{4}{3} e^{2} + \frac{4}{3}] \Rightarrow
$$
$$
V = \frac{2}{3} (e^{2} – 1) \pi.
$$
综上可知,区域 $D$ 的面积 $S = 2$, 区域 $D$ 绕 $x$ 轴旋转一周所得的旋转体的体积 $V = \frac{2}{3} (e^{2} – 1) \pi$.