六、解答题 (本题满分 9 分)
作半径为 $r$ 的球的外切正圆锥, 问此圆锥的高 $h$ 为何值时, 其体积最小, 并求出该最小值.
示意图:
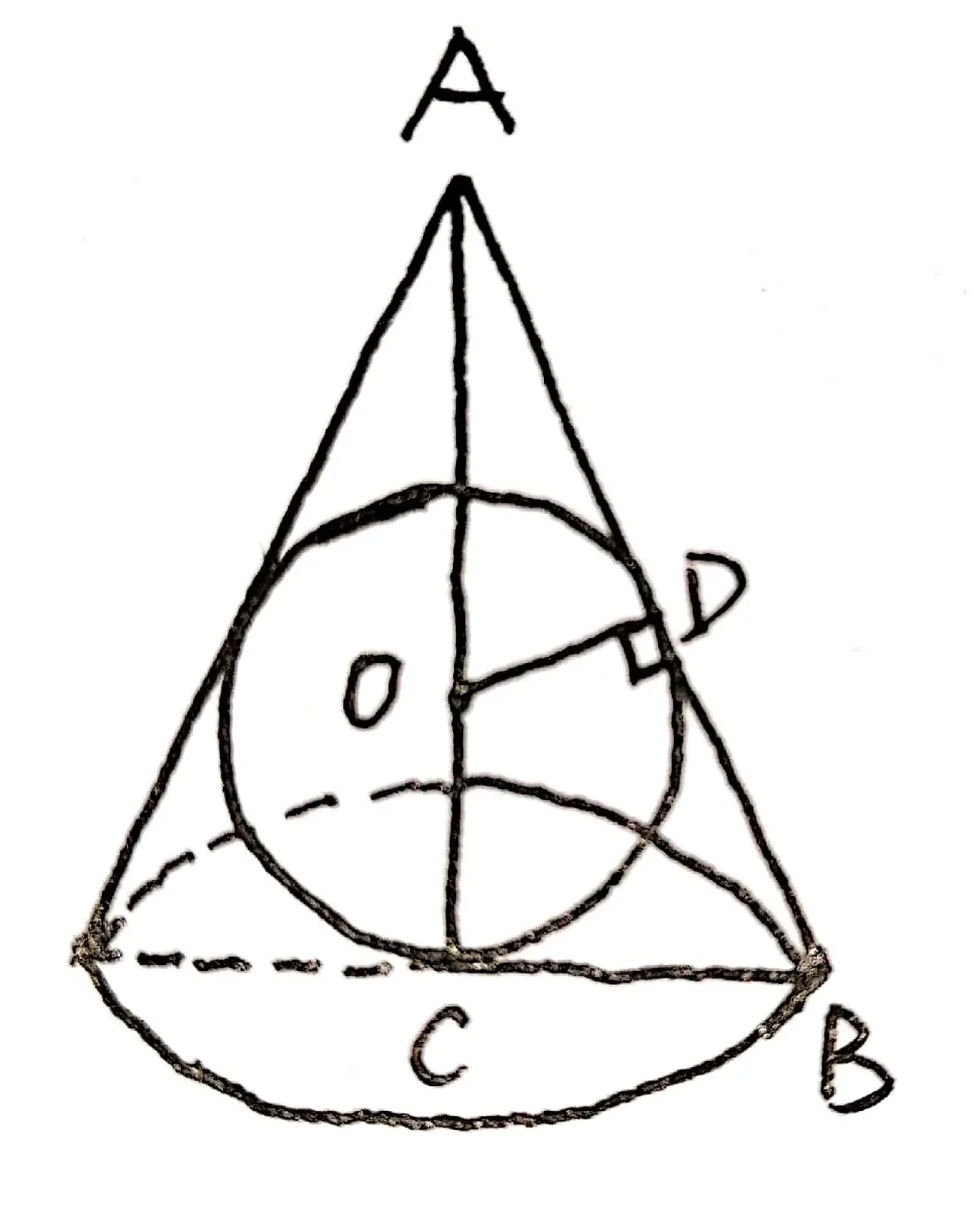
设圆镌祗面半径为R, 则
$$
B C=O D=r
$$
$$
\text { 又设 } A C=h \Rightarrow
$$
$$
\frac{B C}{A C}=\frac{O D}{A D} \Rightarrow \frac{R}{h}=\frac{r}{\sqrt{(h-r)^{2}-r^{2}}} \Rightarrow
$$
$$
R=\frac{r h}{\sqrt{(h-r)^{2}-r^{2}}} \Rightarrow \frac{1}{3} \pi R^{2} \cdot h \Rightarrow
$$
于是:
$$
V=\frac{1}{3} \pi \frac{r^{2} h^{2}}{h-2 r} \Rightarrow
$$
$$
V^{\prime}(h)=\frac{1}{3} \pi r^{2}\left(\frac{h^{2}}{h-2 r}\right)_{h}^{\prime} \Rightarrow
$$
$$
V^{\prime}(h)=\frac{1}{3} \pi r^{2} \cdot \frac{h^{2}-4 h r}{(h-2 r)^{2}} \Rightarrow
$$
$$
V^{\prime}(h)=0 \Rightarrow
$$
$$
h-4 r=0 \Rightarrow h=4 r
$$
由于一定存在最小值,因此,当 $h = 4r$ 时取得的唯一极值一定是最小值:
$$
V(4 r)=\frac{8 \pi r^{3}}{3}
$$