五、解答题 (本题满分 9 分)
设平面图形 $A$ 由 $x^{2}+y^{2} \leqslant 2 x$ 与 $y \geqslant x$ 所确定,求图形 $A$ 绕直线 $x=2$ 旋转一周所得旋转体的体积.
注意:对于旋转体的体积,不能只会用公式计算,还要会用微分的思路计算。
方法一: 视作薄片的体积
示意图:
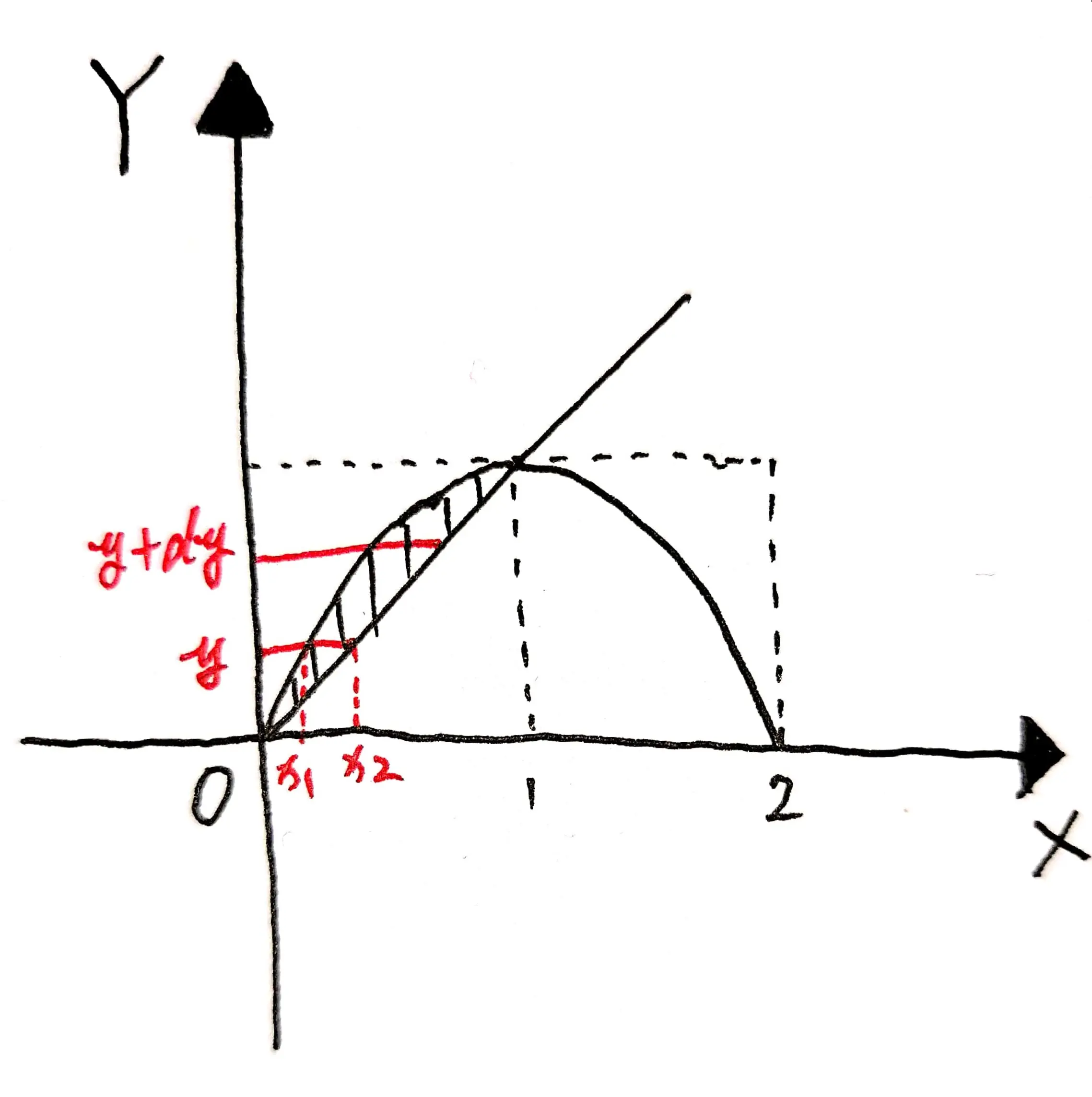
在 $Y$ 轴上进行微分,就找 $x(y)$ 的表达式:
$$
x^{2}+y^{2}=2 x \Rightarrow(x-1)^{2}+y^{2}=1 \Rightarrow
$$
$$
(x-1)^{2}=1-y^{2} \Rightarrow x<1 \Rightarrow-(x-1)=\sqrt{1-y^{2}} \Rightarrow
$$
$$
x_{1}=1-\sqrt{1-y^{2}},
$$
$$
y=x \Rightarrow x_{2}=y
$$
于是,圆柱体的体积可以表示为:
$$
\mathrm{d} V=\pi\left(2-x_{1}\right)^{2} \mathrm{~ d} y-\pi\left(2-x_{2}\right)^{2} \mathrm{~ d} y \Rightarrow
$$
$$
\mathrm{d} V=\pi\left[\left(1+\sqrt{1-y^{2}}\right)^{2}-(2-y)^{2}\right] \mathrm{~ d} y \Rightarrow
$$
$$
\mathrm{d} V=2 \pi\left[\sqrt{1-y^{2}}-(y-1)^{2}\right] \mathrm{~ d} y \Rightarrow
$$
$$
V=2 \pi \int_{0}^{1}\left[\sqrt{1-y^{2}}-(y-1)^{2}\right] \mathrm{~ d} y \Rightarrow
$$
又:
$$
x=\sqrt{1-y^{2}} \Rightarrow x^{2}=1-y^{2} \Rightarrow x^{2}+y^{2}=1 \Rightarrow
$$
$$
\int_{0}^{1} \sqrt{1-y^{2}} \mathrm{~ d} y=\frac{1}{4} \pi
$$
且:
$$
\int_{0}^{1}(y-1)^{2} \mathrm{~ d} y=\left.\frac{1}{3}(y-1)^{3}\right|_{0} ^{1}=\frac{1}{3}(0+1)=\frac{1}{3}
$$
于是:
$$
V=2 \pi\left(\frac{\pi}{4}-\frac{1}{3}\right)=\frac{\pi^{2}}{2}-\frac{2 \pi}{3} .
$$
方法二: 看作薄圆筒
示意图:
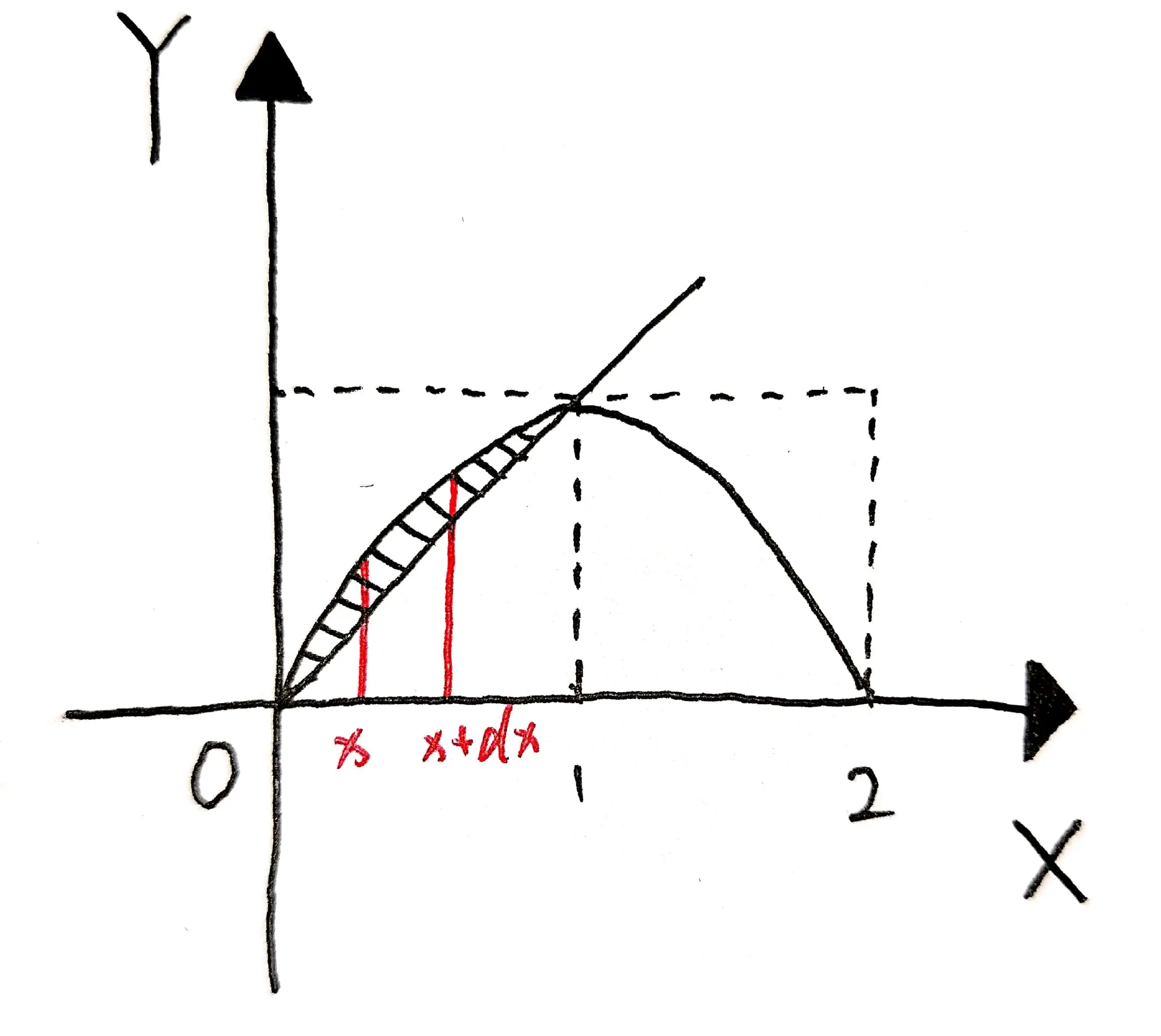
$$
x^{2}+y^{2}=2 x \Rightarrow y_{1} = \sqrt{2 x-x^{2}}, \ y_{2}=x \Rightarrow
$$
于是,将薄圆筒展开之后就是:
$$
\text { 宽: } \mathrm{~ d} x
$$
$$
\text { 长: } 2 \pi r=2 \pi(2-x)
$$
$$
\text { 高: } y_{1}-y_{2}=\sqrt{2 x-x^{2}}-x
$$
于是:
$$
\mathrm{d} V=2 \pi(2-x)\left(\sqrt{2 x-x^{2}}-x\right) \mathrm{~ d} x \Rightarrow
$$
$$
V=2 \pi \int_{0}^{1}\left[(2-x)\left(\sqrt{2 x-x^{2}}-x\right)\right] \mathrm{~ d} x \Rightarrow
$$
$$
V=2 \pi\left[\int_{0}^{1}\left(2 \sqrt{2 x-x^{2}}-x \sqrt{2 x-x^{2}}-\left(2 x-x^{2}\right)\right) \mathrm{~ d} x\right]=
$$
$$
V=2 \pi\left[\int_{0}^{1} \sqrt{2 x-x^{2}} \mathrm{~ d} x+\int_{0}^{1}(1-x) \sqrt{2 x-x^{2}} \mathrm{~ d} x-\right.
$$
$$
\left.\int_{0}^{1}\left(2 x-x^{2}\right) \mathrm{~ d} x\right] \Rightarrow
$$
又:
$$
\int_{0}^{1} \sqrt{2 x-x^{2}}=\frac{1}{4} \pi r^{2}=\frac{\pi}{4}
$$
$$
\int_{0}^{1}(1-x) \sqrt{2 x-x^{2}} \mathrm{~ d} x=\frac{1}{2} \int_{0}^{1}(2-2 x) \sqrt{2 x-x^{2}} \mathrm{~ d} x=
$$
$$
\left.\frac{1}{2} \cdot \frac{2}{3}\left(2 x-x^{2}\right)^{\frac{3}{2}}\right|_{0} ^{1}=\frac{1}{3}
$$
$$
\int_{0}^{1}\left(2 x-x^{2}\right) \mathrm{~ d} x=\left.\left(x^{2}-\frac{1}{3} x^{3}\right)\right|_{0} ^{1}=\frac{2}{3}
$$
于是:
$$
V=\left(\frac{\pi}{4}+\frac{1}{3}-\frac{2}{3} x\right) \cdot 2 \pi=\frac{\pi^{2}}{2}-\frac{2 \pi}{3}
$$