五、解答题 (本题满分 8 分)
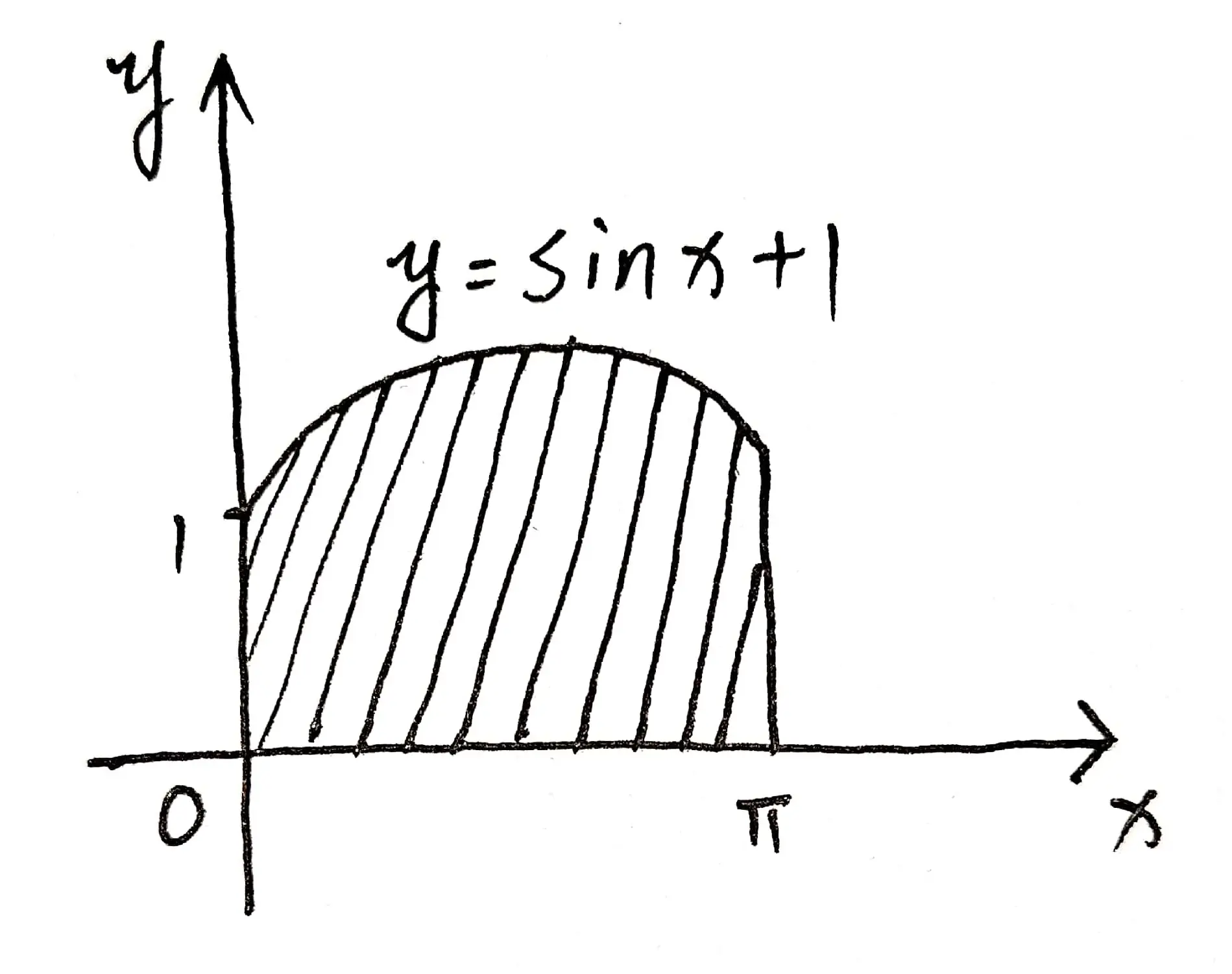
设 $D$ 是由曲线 $y=\sin x+1$ 与三条直线 $x=0, x=\pi, y=0$ 所围成的曲边梯形, 求 $D$ 绕 $O x$ 轴旋转一周所生成的旋转体的体积.
根据题意,我们可以绘制出如图 01 所示的示意图:
$$
V=\pi \int_{0}^{\pi}(\sin x+1)^{2} \mathrm{~ d} x=
$$
$$
\pi \int_{0}^{\pi}\left(\sin ^{2} x+1+2 \sin x\right) \mathrm{~ d} x =
$$
$$
2 \pi \int_{0}^{\frac{\pi}{2}}\left(\sin ^{2} x+1+2 \sin x\right) \mathrm{~ d} x=
$$
$$
2 \pi\left(\frac{1}{2} \cdot \frac{\pi}{2}+\frac{\pi}{2}-\left.2 \cos x\right|_{0} ^{\frac{\pi}{2}}\right]=
$$
$$
2 \pi\left(\frac{\pi}{4}+\frac{\pi}{2}-2(0-1)\right]=\frac{3 \pi^{2}}{2}+4 \pi
$$