一、题目
已知,可微函数 $f(x, y)$ 满足 $\frac{\partial f}{\partial x}>1$, $\frac{\partial f}{\partial y}<-1$, $f(0,0)=0$, 则下列结论正确的是
(A) $f(1,-1)>2$.
(B) $f(-1,1)>-2$.
(C) $f(-1,-1)<0$.
(D) $f(1,1)>1$.
难度评级:
二、解析 
方法一:画图法
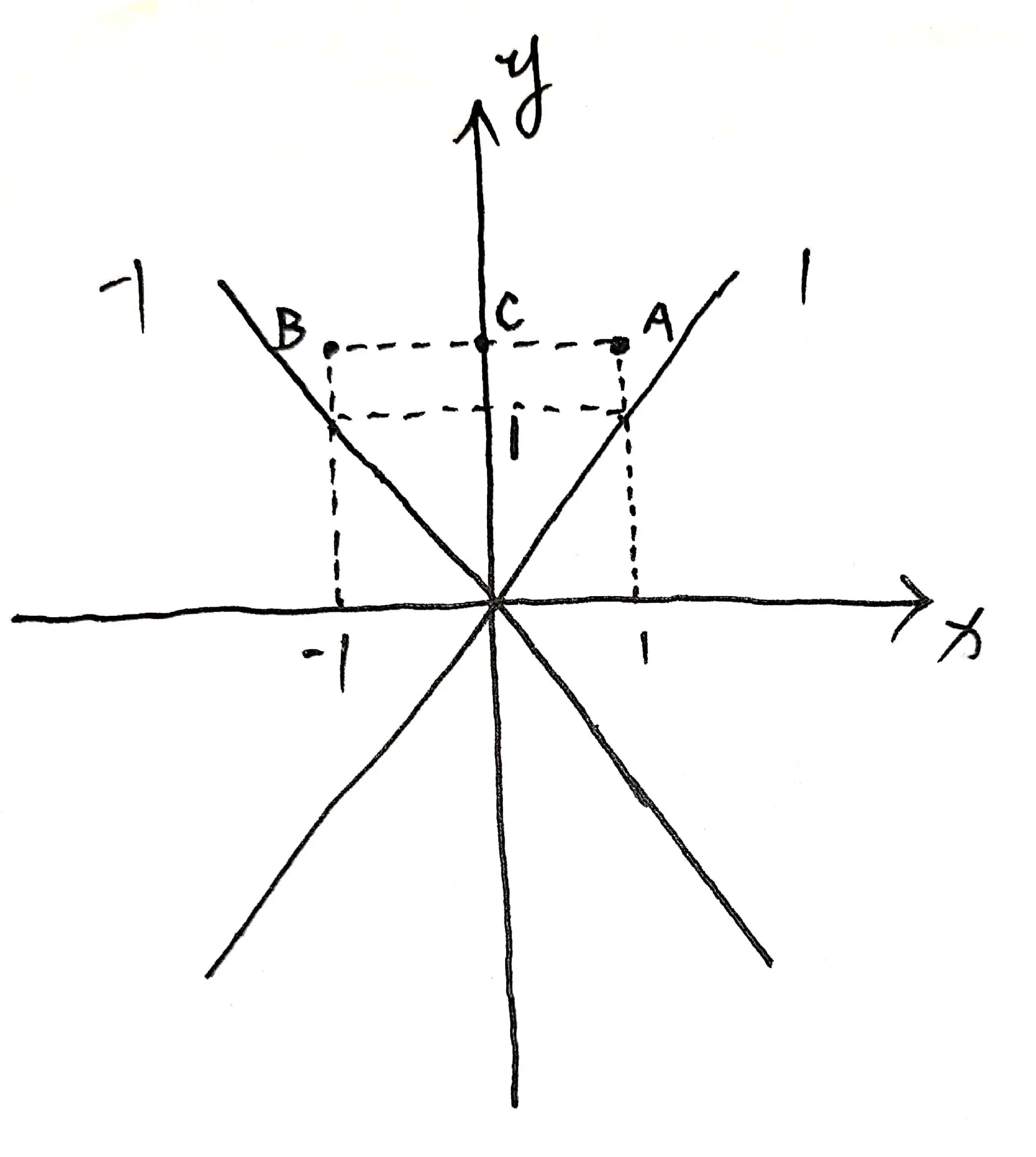
如图 01 所示,图中两条实直线的斜率分别是 $1$ 和 $-1$,则由 $\frac{\partial f}{\partial x}>1$ 可知,$f$ 应该经过 $A$ 点,又由 $\frac{\partial f}{\partial y}<-1$ 可知,$f$ 还应该经过 $B$ 点,对应的函数值都是 $C$ 点,且:
$$
C > 1
$$
则可知:
$$
f(1, -1) > 2
$$
即,(A) 选项正确。
方法二:拉格朗日中值定理
(A) 选项:
$$
f(1,-1)=f(1,-1)-f(0,0)=
$$
$$
{[f(1,-1)-f(0,-1)]+[f(0,-1)-f(0,0)] \Rightarrow}
$$
根据拉格朗日中值定理可知:
$$
\frac{f(b)-f(a)}{b-a}=f^{\prime}(\xi), \quad \xi \in(a, b)
$$
于是:
$$
\frac{f(1,-1)-f(0,-1)}{1-0}=f_{x}^{\prime}(\xi), \quad \xi \in(0,1) \Rightarrow
$$
$$
f(1,-1)-f(0,-1)=f_{x}^{\prime}(\xi,-1) \Rightarrow
$$
$$
\frac{f(0,-1)-f(0,0)}{-1-0}=f_{y}^{\prime}(\eta), \eta \in(-1,0) \Rightarrow
$$
$$
f(0,-1)-f(0,0)=-f_{y}^{\prime}(0, \eta)
$$
即:
$$
f(1,-1)=f_{x}^{\prime}(\xi,-1)-f_{y}^{\prime}(0, \eta)>1-(-1)=2
$$
(B) 选项:
$$
f(-1,1)=f(-1,1)-f(0,0)=
$$
$$
{[f(-1,1)-f(0,1)]+[f(0,1)-f(0,0)]=}
$$
$$
-f_{x}^{\prime}(\xi, 1)+f_{y}^{\prime}(0, \eta)<-1-1=-2
$$
(C) 选项:
$$
f(-1,-1)=f(-1,-1)-f(0,0)=
$$
$$
{[f(-1,-1)-f(-1,0)]+[f(-10,0)-f(0,0)]=}
$$
$$
-f_{y}^{\prime}(-1, \xi)-f_{x}^{\prime}(1,0)<0 \quad \text { 或者 }>0
$$
(D) 选项:
$$
f(1,1)=f(1,1)-f(0,0)=
$$
$$
{[f(1,1)-f(1,0)]+[f(1,0)-f(0,0)]=}
$$
$$
f_{y}^{\prime}(1, \xi)+f_{x}^{\prime}(0,0)>1 \text { 或者 }<1
$$
综上可知,(A) 选项正确。
方法二:特例法
另:
$$
f(x, y)=1.1 x-1.1 y
$$
则:
$$
(A) \Rightarrow f(1,-1)=1.1+1.1>2
$$
$$
(B) \Rightarrow f(-1,1)=-1.1-1.1=-2,2<-2
$$
$$
(C) \Rightarrow f(-1,-1)=-1.1+1.1=0 \nless 0
$$
$$
(D) \Rightarrow f(1,1)=1.1-1.1 = 0 < 1
$$
综上可知,(B), (C), (D) 选项都可以被排除,只能选 (A).