计算平行截面面积已知的立体体积（B007）

问题

如下图所示，若已知 $S(x)$ 为某立体垂直于 $x$ 轴的截面面积函数，则，如何使用定积分表示该立体在 $x$ $=$ $a$ 和 $x$ $=$ $b$ ($a$ $<$ $b$) 两个截面之间的体积 $V$ ?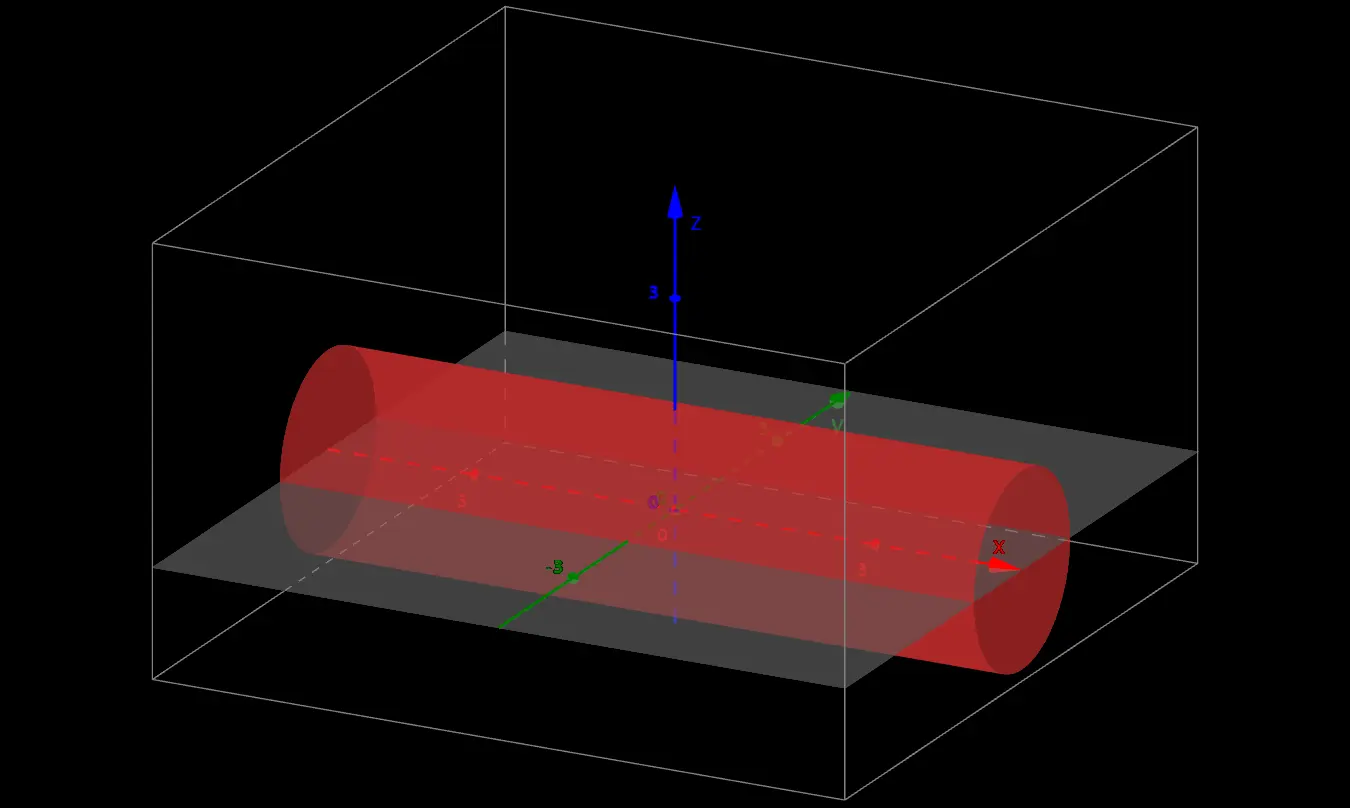

选项

[A].   $V$ $=$ $\int_{a}^{b}$ $|S(x)|$ $\mathrm{d} x$

[B].   $V$ $=$ $\int_{b}^{a}$ $S(x)$ $\mathrm{d} x$

[C].   $V$ $=$ $\int_{a}^{b}$ $S(x)$ $\mathrm{d} x$

[D].   $V$ $=$ $\int_{a}^{b}$ $S^{2}(x)$ $\mathrm{d} x$

   答 案   

$V$ $=$ $\int_{\textcolor{orange}{a}}^{\textcolor{orange}{b}}$ $\textcolor{red}{S(x)}$ $\mathrm{d} x$