题目
编号:A2016205
设函数 $f_{i}(x) (i=1,2)$ 具有二阶连续导数,且 $f_{i}^{”}(x_{0}) < 0 (i=1,2)$. 若两条曲线 $y=f_{i}(x) (i=1,2)$ 在点 $(x_{0}, y_{0})$ 处具有公切线 $y=g(x)$, 且在该点处曲线 $y=f_{1}(x)$ 的曲率大于 $y=f_{2}(x)$ 的曲率,则在 $x_{0}$ 的某个邻域内,有 $?$
$$
A. f_{1}(x) \leqslant f_{2}(x) \leqslant g(x)
$$
$$
B. f_{2}(x) \leqslant f_{1}(x) \leqslant g(x)
$$
$$
C. f_{1}(x) \leqslant g(x) \leqslant f_{2}(x)
$$
$$
D. f_{2}(x) \leqslant g(x) \leqslant f_{1}(x)
$$
解析
方法一:
当两个函数都是对应凸曲线(都是凹曲线也一样)时,他们两个如果想相切,那么一定是一个曲线嵌套在另外一个曲线中产生的相切,即这两条曲线必须在切线的一侧。否则,如果是普通情况下的相切,即这两条曲线位于切线的两侧,那么这两条曲线就不是由两个函数形成的曲线了,因为,“函数”要求一个自变量 $x$ 只能对应一个因变量 $y$.
于是,我们有了如图 1 所示的函数 $f_{1}(x)$, $f_{2}(x)$ 和切线 $g(x)$ 的示意图:
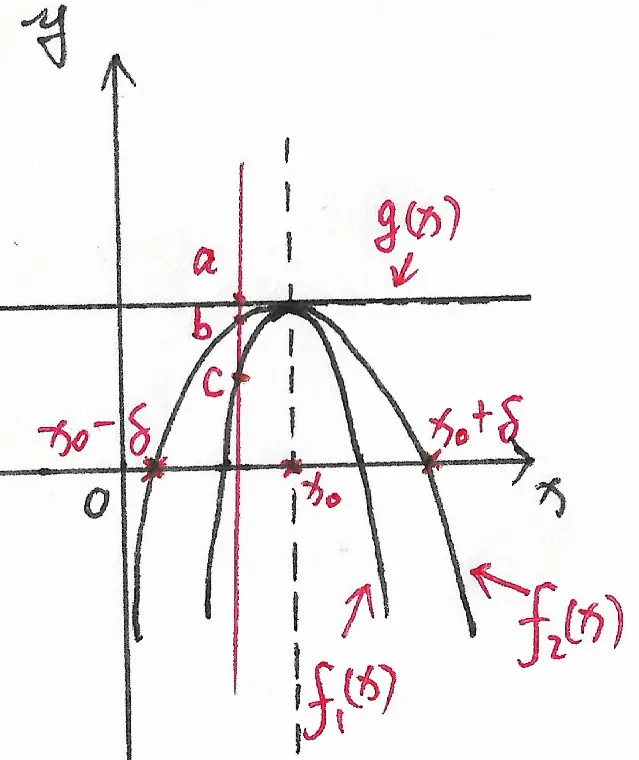
由于曲率越大表示弯曲程度越大,因此,在图 1 中我们可以看到,$f_{1}(x)$ 比 $f_{2}(x)$ 更加弯曲。
图 1 中画出的切线 $g(x)$ 是水平的,当切线不是水平的时候,图中 $a$, $b$, $c$ 三个点的上下位置仍然不变。
由图 1 可以看出,在邻域 $(x_{0} – \delta, x_{0} + \delta)$ 中,显然有:
$$
g(x) > f_{2}(x) > f_{1}(x).
$$
又由于当 $x=x_{0}$ 时也会存在 $g(x_{0}) = f_{2}(x_{0}) = f_{1}(x_{0})$ 的情况($x=x_{0}$ 处相切,因此函数值一定相等),并且所有选项中都包含 $”=”$ 符号,因此,正确答案就是 $A$.
汤家凤老师曾在某年讲真题时说 2016 年的第 5 题是比较难的一题,但我们可以发现,用上面这种方法解本题就很简单——上面的解题过程并不严谨,但这是【考试试卷】中的【选择题】,只要能通过构造的特例找出正确答案就可以了。
用下面的法二解本题就有点难了。
方法二:
该方法就是使用曲率公式计算。
曲率的计算公式为:
$$
K=\frac{|y^{”}|}{(1+y^{‘2})^{\frac{3}{2}}} \geqslant 0.
$$
由于 $f_{1}(x)$, $f_{2}(x)$, $g(x)$ 三条曲线相切,于是有:
$$
f_{1}(x_{0}) = f_{2}(x_{0}) = g(x_{0}). (1)
$$
$$
f_{1}^{‘}(x_{0}) = f_{2}^{‘}(x_{0}) = g^{‘}(x_{0}). (2)
$$
又:
$$
f_{1}^{”}(x_{0}) < 0.
$$
$$
f_{2}^{”}(x_{0}) < 0.
$$
于是:
$$
\frac{-f_{1}^{”}(x_{0})}{[1+f_{1}^{‘2}(x_{0})]^{\frac{3}{2}}} > \frac{-f_{2}^{”}(x_{0})}{[1+f_{2}^{‘2}(x_{0})]^{\frac{3}{2}}}.
$$
即,在 $x_{0}$ 的邻域内,有:
$$
f_{1}^{”}(x) < f_{2}^{”}(x) < 0. (3)
$$
又由于切线 $y = g(x)$ 是一条直线,直线的一阶导一定是常数,直线的二阶导一定为 $0$, 因此有:
$$
g^{”}(x) = 0. (4)
$$
结合 $(3)$, $(4)$ 两个式子,于是有:
$$
f_{1}^{”}(x) < f_{2}^{”}(x) < g^{”}(x) = 0. (5)
$$
则,$\exists \delta > 0$, 当 $0 < |x-x_{0}| < \delta$ 时,设:
$$
\varphi(x) = g^{‘}(x) – f_{2}^{‘}(x). (6)
$$
于是有:
$$
\varphi^{‘}(x) = g^{”}(x) – f_{2}^{”}(x).
$$
结合 $(3)$ 式可知:
$$
\varphi^{‘}(x) > 0.
$$
于是可知,$\varphi(x)$ 在邻域 $(x_{0} – \delta, x_{0} + \delta)$ 上为增函数。
又结合 $(2)$, $(6)$ 两个式子知:
$$
\varphi(x_{0}) = 0.
$$
于是,当 $x \in (x_{0} – \delta, x_{0})$ 时,有:
$$
\varphi(x) < 0 \Rightarrow
$$
$$
g^{‘}(x) \leqslant f_{2}^{‘}(x).
$$
注意:一个区间内有限个点对应的函数值相等并不影响该区间内函数的增减性。所以,上式中含有 $”=”$ 符号。
当 $x \in (x_{0}, x_{0} + \delta)$ 时,有:
$$
\varphi(x) > 0 \Rightarrow
$$
$$
g^{‘}(x) \geqslant f_{2}^{‘}(x).
$$
于是:
在 $x_{0}$ 的左邻域 $(x_{0} – \delta, x_{0})$ 内,$g(x)$ 的增长速度小于 $f_{2}(x)$ 的增长速度,但当 $f_{2}(x)$ 从 $x=x_{0} – \delta$ 追赶 $g(x)$ 到 $x=x_{0}$ 时,恰好抵达相同的“终点” $f_{2}(x_{0}) = g(x_{0})$.
因此,我们知道,在一开始的时候,跑得慢的 $g(x)$ 必须在跑得快的 $f_{2}(x)$ 的上面,于是,在邻域 $(x_{0} – \delta, x_{0})$ 内,只可能有:
$$
g(x) \geqslant f_{2}(x).
$$
在 $x_{0}$ 的右邻域 $(x_{0}, x_{0} + \delta)$ 内,$g(x)$ 的增长速度大于 $f(x)$ 的增长速度。由于此时,$f_{2}(x)$ 和 $g(x)$ 的“起点”是一样的,都是 $f_{2}(x_{0}) = g(x_{0})$, 因此,“起点”一样时,增长得快的一定大于增长得慢的。即,在邻域 $(x_{0} – \delta, x_{0})$ 内,只可能有:
$$
g(x) \geqslant f_{2}(x).
$$
于是,在 $x \in (x_{0} – \delta, x_{0} + \delta)$ 内,有:
$$
g(x) \geqslant f_{2}(x).
$$
同理可得:
$$
f_{2}(x) \geqslant f_{1}(x).
$$
即:
$$
g(x) \geqslant f_{2}(x) \geqslant f_{1}(x).
$$
综上可知,正确选项为 $A$.
EOF