一、性质
$A$ 与 $B$ 为互斥(互不相容)事件 $\Leftrightarrow$ $A$ $\cap$ $B$ $=$ $\varnothing$ $\Leftrightarrow$ $A$ 与 $B$ 不能同时发生。
$A$ 与 $B$ 为对立(互逆)事件 $\Leftrightarrow$ $A$ $\cap$ $B$ $=$ $\varnothing$ 且 $A$ $\cup$ $B$ $=$ $\Omega$ $\Leftrightarrow$ $A$ 与 $B$ 在一次试验中必然发生且只能发生一个。
若 $P(A)$ $=$ $0$ 或 $P(A)$ $=$1$, 则 $A$ 与任何事件都相互独立。
若 $A$ 与 $B$ 相互独立,则 $P(AB)$ $=$ $P(A)P(B)$.
若 $A$ 与 $B$ 互斥(或互逆)且均为非零概率事件,则 $A$ 与 $B$ 不相互独立。
若 $A$ 与 $B$ 相互独立且均为非零概率事件,则 $A$ 与 $B$ 不互斥。
二、图解
$A$ 与 $B$ 互斥(互不相容)关系如图 1 所示:
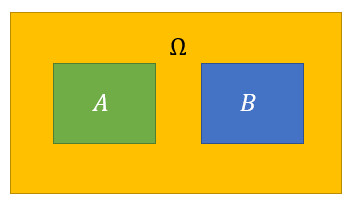
$A$ 与 $B$ 对立(互逆)关系如图 2 所示:
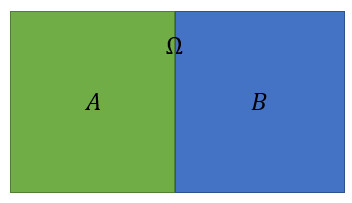
$A$ 与 $B$ 相互独立关系如图 3 所示:

$A$ 与 $B$ 互逆,互斥与独立之间的推导关系如图 4 所示:

EOF