[线代]行满秩列满秩与满秩在矩阵乘法中的几条性质

一、名词解释

1. 行 满 秩

矩阵有效的行数，也就是线性无关的行的个数。

2. 列 满 秩

矩阵有效的列数，也就是线性无关的列的个数。

3. 满 秩

一个矩阵行满秩或者列满秩（满足一个即可）就称为满秩矩阵。

这里需要注意的是，并不是只有方阵才能满秩。因为“满秩”说的是一个矩阵中最大的非零 $n$ 阶方阵的阶数 $n$, 很显然，只要一个矩阵行满秩（列满秩），那么这个矩阵内部就不会存在阶数大于其行数（列数）的方阵了，自然也不会存在阶数大于其行数（列数）的非零方阵。

4. 行 秩 $\textcolor{red}{=}$ 列 秩 $\textcolor{red}{=}$ 秩

无论一个行列式是否是行满秩或列满秩矩阵，都有如下性质：

行秩 $=$ 列秩 $=$ 秩。

对此我们可以这样理解：由于转置并不改变矩阵的秩，因此必然有“行秩 $=$ 列秩”。

二、性质

若 $A$ 【行】满秩，则：

$$
R(BA)=R(B).
$$

若 $A$ 【列】满秩，则：

$$
R(AB)=R(B).
$$

三、性质解释

下面对上述性质的解释并不是严格的数学推导，而是通过合理的思考方式，在能够自圆其说的情况下，对上述性质做形象化的解释以帮助记忆和使用上述性质。

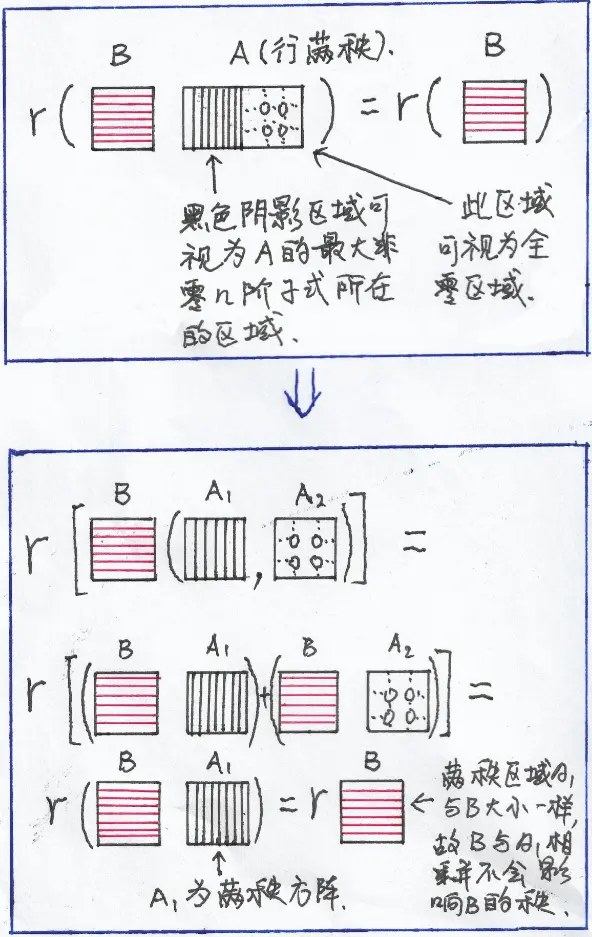
当 $A$ 【行】满秩时，对 $R(BA)=R(B)$ 的理解为：

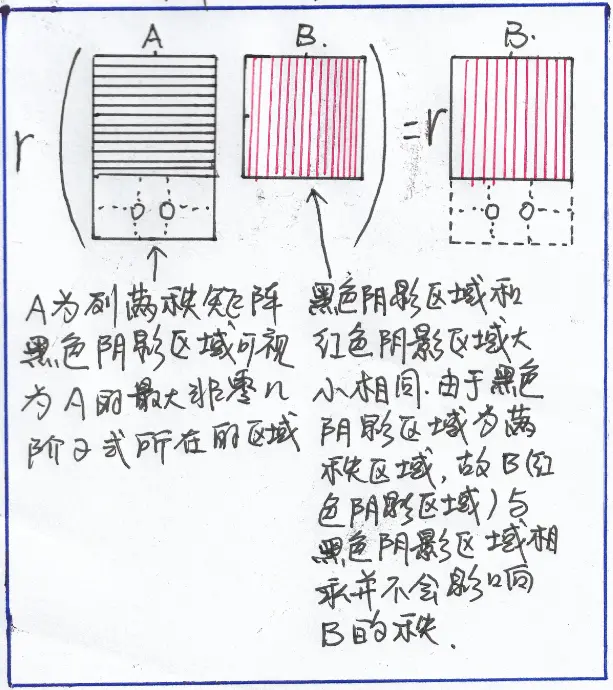
当 $A$ 【列】满秩时，对 $R(AB)=R(B)$ 的理解为：

---

EOF