题目
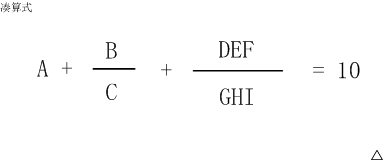
凑算式
B DEF A + --- + ------- = 10 C GHI
(如果显示有问题,可以参见【图1.jpg】)
这个算式中A~I代表1~9的数字,不同的字母代表不同的数字。
比如:
6+8/3+952/714 就是一种解法,
5+3/1+972/486 是另一种解法。
这个算式一共有多少种解法?
注意:你提交应该是个整数,不要填写任何多余的内容或说明性文字。
题目分析
本题就是一个无重复全排列的问题, 在 C++ 中实现无重复全排列有以下两种主要方式:
- 通过
next_permutation()函数实现全排列
next_permutation() 全排列函数只能对有序数列的数组进行全排列, 示例如下:
#include<iostream>
#include<bits/stdc++.h>
using namespace std;
int main(){
int a[3]={0,1,2};
while(next_permutation(a,a+3)){
cout<<a[0]<<a[1]<<a[2];
cout<<endl;
}
return 0;
}
- 通过循环实现全排列
假设我们要对从 1 到 3 这个三个数字进行全排列, 那么我们可以使用如下的方式进行:
#include<iostream>
#include<bits/stdc++.h>
using namespace std;
int main(){
for(int a=1;a<=3;a++){
for(int b=1;b<=3;b++){
if(b!=a){
for(int c=1;c<=3;c++){
if(c!=a&&c!=b){
cout<<a<<" "<<b<<" "<<c<<endl;
}
}
}
}
}
return 0;
}
另外, 在本题中需要注意的是, 本题给出的算式是存在除法的, 涉及除法就不得不考虑精度的问题. 为了解决精度的问题, 一方面我们可以使用将整型强制转换成 double 型的方式, 另一方面也可以使用将除法转换成乘法的方式进行计算.
根据上面的分析, 我们可以有两种方法计算本题.
方法一: 使用 C++ 中的 next_permutation() 函数计算, 程序如下:
#include<iostream>
#include<bits/stdc++.h> //万能头文件, 包含所有函数
using namespace std;
int main(){
int a[9]={1,2,3,4,5,6,7,8,9};
int sum=0;
while(next_permutation(a,a+9)){
//对数组a的前9个元素进行全排列, 也就是对全部元素进行全排列
double sum2=(double)a[0]+(double)a[1]/a[2]+double(a[3]*100+a[4]*10+a[5])/(a[6]*100+a[7]*10+a[8]);
if(sum2==10.0){
sum++;
}
}
cout<<sum<<endl;;
return 0;
}
方法二: 使用九层 for 循环计算, 程序如下:
#include<iostream>
#include<bits/stdc++.h>
using namespace std;
int main(){
int ans=0;
for(int a=1;a<=9;a++){
for(int b=1;b<=9;b++){
if(b!=a){
for(int c=1;c<=9;c++){
if(c!=a&&c!=b){
for(int d=1;d<=9;d++){
if(d!=a&&d!=b&&d!=c){
for(int e=1;e<=9;e++){
if(e!=a&&e!=b&&e!=c&&e!=d){
for(int f=1;f<=9;f++){
if(f!=a&&f!=b&&f!=c&&f!=d&&f!=e){
for(int g=1;g<=9;g++){
if(g!=a&&g!=b&&g!=c&&g!=d&&g!=e&&g!=f){
for(int h=1;h<=9;h++){
if(h!=a&&h!=b&&h!=c&&h!=d&&h!=e&&h!=f&&h!=g){
for(int i=1;i<=9;i++){
if(i!=a&&i!=b&&i!=c&&i!=d&&i!=e&&i!=f&&i!=g&&i!=h){
double sum2=(double)a+(double)b/c+double(d*100+e*10+f)/(g*100+h*10+i);
if(sum2==10.0){
ans++;
}
}
}
}
}
}
}
}
}
}
}
}
}
}
}
}
}
}
cout<<ans<<endl;
return 0;
}