前言
Z-BlogPHP 是一款常用的 Web 博客程序, 许多网站都是使用 Z-BlogPHP 搭建的. 今天, 我来结合自己目前所掌握的知识谈谈对使用 Z-BlogPHP 搭建的网站进行安全加固的方法. 希望本文能让更多的网站尽可能地远离安全威胁.
网站加固涉及很多方面, 有 Web 程序的加固, 中间件的加固, 代码运行环境的加固, 还有 Web 服务器的加固等, 本文只讨论对 Web 程序, 也就是 Z-BlogPHP 本身的加固.
操作环境
Z-BlogPHP 版本: Z-BlogPHP 1.5.2 Zero 正式版
加固步骤
保护登录入口
使用 Google 两步验证
两步验证相当于给登录过程加了两把锁, 即使我们网站的登录密码被恶意获取和利用, 攻击者也无法仅仅依靠该密码就成功登录网站后台. 两步验证的实现方式中常用的大致有两种:
使用”手机短信验证码”的方式进行验证就是在登录的时候除了要输入用户名和密码之外还会要求输入一个由服务器发来的手机短信. 虚拟 MFA 的作用和手机短信验证码类似, 只不过虚拟 MFA 可以基于时间 (或者计数器) 生成验证码 (每 30 秒自动生成一个 6 位数字), 不需要联网即可运作.
目前可以提供虚拟 MFA 验证的软件有:
Authy 1Password Microsoft Authenticator Google 2-Step Verification 想要在 Z-BlogPHP 中使用两步验证, 首先需要在 Z-BlogPHP 的应用中心搜索”Google两步验证”找到相关插件, 插件 ID 是”LiangbuLogin”. 下载完成之后, 启用该插件.
下面我在手机上使用 Google 两步验证程序”Google 身份验证器”和 Z-BlogPHP 中的”Google两步验证”插件演示配置并启用两步验证的过程.
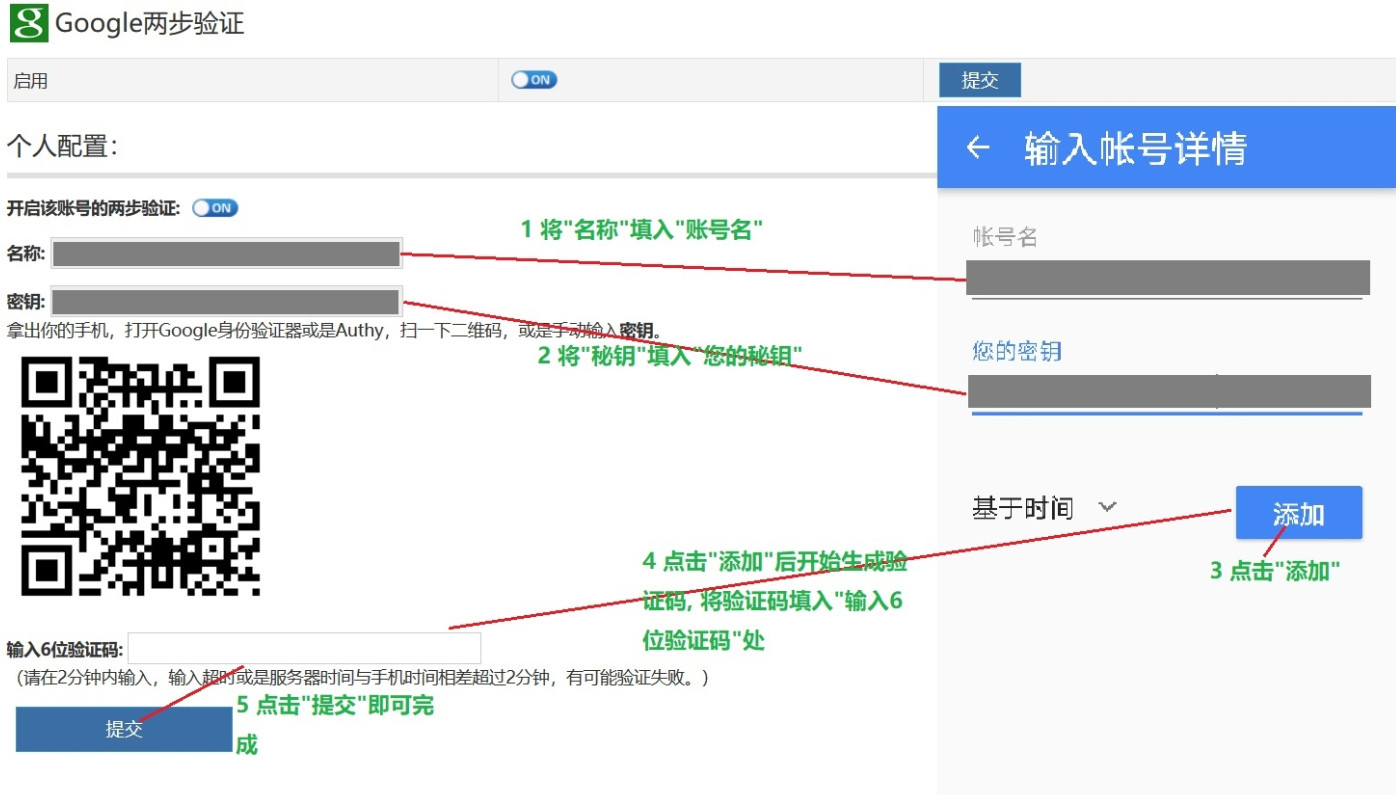
首先, 在 Z-BlogPHP 的管理后台中进入”Google两步验证”插件的配置界面并打开手机上的”Google 身份验证器”, 之后的操作过程如图 1 所示:
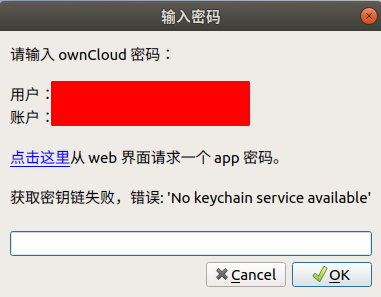
图 1 之后, 再登陆 Z-BlogPHP 的后台时会要求输入 Google 两步验证的验证码, 如图 2 所示.
图 2 如果进行两步验证的设备丢失, 可以在服务上删除如下目录及文件即可取消 Google 两步验证:
XX/zb_users/plugin/LiangbuLogin
另外, 需要注意的是, 如果设备支持的话, 请务必给进行两步验证的程序加上应用锁以尽可能避免未经授权的使用.
修改默认登录地址
Z-BlogPHP 默认的登录地址如下:
https://域名/zb_system/login.php
如果使用默认的登录地址的话, 就是把网站登录入口直接暴露在攻击者面前, 这是一个严重的不安全因素. 下面演示修改默认登录地址的方法.
首先将 zb_system/ 目录下的 login.php 文件修改成一个随机名称, 例如: ajdvirb6zmg9s7k2.php, 之后, 登录地址就变成了:
https://域名/zb_system/ajdvirb6zmg9s7k2.php
下一步, 在当前网站所使用的主题 (一般位于 xx/zb_users/theme/ 目录下) 下面找到 include.php 这个文件, 在其中加入如下 PHP 代码:
#修改默认登录地址
function zpnfewmcbxgsak(){
global $zbp;
$sfwidmsahdgv="ssocnf7sbsnxs";
$dsdsuacskpqba="sdvn2ps3m2n";
if($_GET[''.$sfwidmsahdgv.''] !== ''.$dsdsuacskpqba.'') {
Redirect($zbp->host);
die();
}
}
之后, 同样在 include.php 这个文件中, 找到 function ActivePlugin_主题 ID(){} 函数, 在其中加入如下 PHP 代码:
Add_Filter_Plugin('Filter_Plugin_Login_Header','zpnfewmcbxgsak');
经过上述操作之后, 登录地址就变成了:
https://域名/zb_system/ajdvirb6zmg9s7k2.php?ssocnf7sbsnxs=sdvn2ps3m2n
上面地址中的任意一个字符不对都将无法打开登录页面.
需要注意的一点是, Z-BlogPHP 默认会把后台登录地址显示在网站前台, 这个组件一定要去掉.
修改登录页面默认标题和内容
通常情况下, 登录页面都会有一些和登录相关的关键词, 例如”登录”, “用户登录”, “login”, “网站后台”, “用户名”和”密码”等. 如果登录界面被搜索引擎爬取到了, 那么攻击者通过类似”Google hack”这样的方式就有可能获取网站登录后台的地址. 因此, 有必要把登录页面的一些关键词修改成和”登录”以及”网站后台”无关的内容. 修改方法如下:
打开 zb_system/ 目录下的 login.php 文件(如果您按照上面的过程进行了修改, 那么此时, 这个文件的名称应该是 ajdvirb6zmg9s7k2.php, 具体名称以您的修改操作为准.), 进行如下修改:
修改用户名输入框的提示字符, 将:
<dd class="username"><label for="edtUserName"><?php echo $lang['msg']['username'] ?></label><input type="text" id="edtUserName" name="edtUserName" size="20" value="<?php echo GetVars('username', 'COOKIE') ?>" tabindex="1" /></dd>
修改成:
<dd class="username"><label for="edtUserName"><?php echo "hskVex" ?></label><input type="text" id="edtUserName" name="edtUserName" size="20" value="<?php echo GetVars('username', 'COOKIE') ?>" tabindex="1" /></dd>
修改密码输入框的提示字符, 将:
<dd class="password"><label for="edtPassWord"><?php echo $lang['msg']['password'] ?></label><input type="password" id="edtPassWord" name="edtPassWord" size="20" tabindex="2" /></dd>
修改成:
<dd class="password"><label for="edtPassWord"><?php echo "sFhfc" ?></label><input type="password" id="edtPassWord" name="edtPassWord" size="20" tabindex="2" /></dd>
修改页面标题, 将:
<title><?php echo $blogname . '-' . $lang['msg']['login'] ?></title>
修改成:
<title><?php echo "HFxs&3^k" . '-' . "pJ18&qxF" ?></title>
修改登录界面的图片标题和图片说明, 将:
<div class="logo"><img src="image/admin/none.gif" title="<?php echo htmlspecialchars($blogname) ?>" alt="<?php echo htmlspecialchars($blogname) ?>"/></div>
修改成:
<div class="logo"><img src="image/admin/none.gif" title="<?php echo "DshjFac@1A7%" ?>" alt="<?php echo "DsE2vshKw7" ?>"/></div>
修改”保持登录”提示字符, 将:
<dd class="checkbox"><input type="checkbox" name="chkRemember" id="chkRemember" tabindex="98" /><label for="chkRemember"><?php echo $lang['msg']['stay_signed_in'] ?></label></dd>
修改成:
<dd class="checkbox"><input type="checkbox" name="chkRemember" id="chkRemember" tabindex="98" /><label for="chkRemember"><?php echo "Qh1A2s$sAv%gC*" ?></label></dd>
修改登录按钮, 将:
<dd class="submit"><input id="btnPost" name="btnPost" type="submit" value="<?php echo $lang['msg']['login'] ?>" class="button" tabindex="99"/></dd>
修改成:
<dd class="submit"><input id="btnPost" name="btnPost" type="submit" value="<?php echo "HCL9" ?>" class="button" tabindex="99"/></dd>
记录访问登录页面的 IP 地址
对于记录 IP 地址这个功能, 我们可以使用第三方的网站统计服务来实现. 我们可以申请一个统计代码, 而且只将这个统计代码放在登录页面, 这样就可以记录到所有访问过登录界面的 IP 地址, 根据这些 IP 地址和登陆时间就可以大致判断网站的登录界面是否已经被攻击者掌握. 但是, 使用第三方服务也就意味着我们的后台登录地址将上传到第三方平台的服务器, 从而增大了后台登录地址可能受到攻击的攻击面, 在这里我们通过一段 PHP 代码实现对访问了登录页面的 IP 地址进行记录的功能.
打开 zb_system/ 目录下的 login.php 文件(如果您按照上面的过程进行了修改, 那么此时, 这个文件的名称应该是 ajdvirb6zmg9s7k2.php, 具体名称以您的修改操作为准.), 添加如下代码:
<?php
$ip = $_SERVER["REMOTE_ADDR"];
$var = "$ip;\n";
file_put_contents('ip.md', $var, FILE_APPEND | LOCK_EX);
?>
上述代码将在当前路径下创建 ip.md 文件并将带有当前访问者 IP 地址的变量 $var 的值以追加的方式 (使用参数 FILE_APPEND 实现内容追加) 写入到 ip.md 文件. 今后, 我们可以通过 ip.md 文件记录的内容获知是否有未授权的 IP 地址打开过登录界面.
使用强登录密码
这一点无需多言, 登录密码至少需要有 16 位, 且必须包括大小写字母, 数字和特殊字符并经常更换.
启用 Z-BlogPHP 自带的安全设置
在 Z-BlogPHP 的管理后台的”网站设置 / 全局设置”中开启”安全增强”并关闭”开发模式”, 如图 3:
图 3 在安装完必要的插件之后, 在 Z-BlogPHP 的管理后台的”应用中心 / 安全模式”中开启安全模式, Z-BlogPHP 建议我们不要使用可以进行文件管理, 数据库管理, 主题编辑和网站备份的插件, 如图 4:
图 4 如果要退出安全模式, 需要进入网站的服务器端, 手动删除以下文件:
/zb_users/data/appcentre_security_mode.php
之后, 在网站后台中进入”插件管理”, 停止”应用中心客户端”的运行. 今后只需要每隔特定时间检查一次更新或者在获知有新版本的程序发布时开启”应用中心客户端”进行一下更新即可.
防止恶意上传
由于我使用 Z-BlogPHP 搭建的网站中主要使用的图片是 .webp 格式, 除此之外基本没有上传过其他格式的文件, 因此可以在后台去掉对不常用的文件格式的上传支持. Z-BlogPHP 默认支持的上传格式如下:
jpg|gif|png|jpeg|bmp|psd|wmf|ico|rpm|deb|tar|gz|sit|7z|bz2|zip|rar|xml|xsl|svg|svgz|rtf|doc|docx|ppt|pptx|xls|xlsx|wps|chm|txt|pdf|mp3|mp4|avi|mpg|rm|ra|rmvb|mov|wmv|wma|swf|fla|torrent|apk|zba|gzba
我修改后的支持的上传格式如下 (在管理后台的”网站设置 / 全局设置”中可以进行修改):
webp|jpg|gif|png|jpeg|bmp
总之, 将允许上传的文件格式限制得越少越好.
删除不必要的文件
Z-BlogPHP 的安装程序在 zb_install 目录下, 安装完成后 zb_install 这个目录及其下的所有文件都可以直接删除以减少网站的受攻击面 (该删除操作不会影响网站的正常登陆和访问).