七、解答题 (本题满分 9 分)
求曲线 $y=\sqrt{x}$ 的一条切线 $l$, 使该曲线与切线 $l$ 及直线 $x=0, x=2$ 所围成图形面积最小.
首先,根据题目,我们可以绘制出如下示意图:
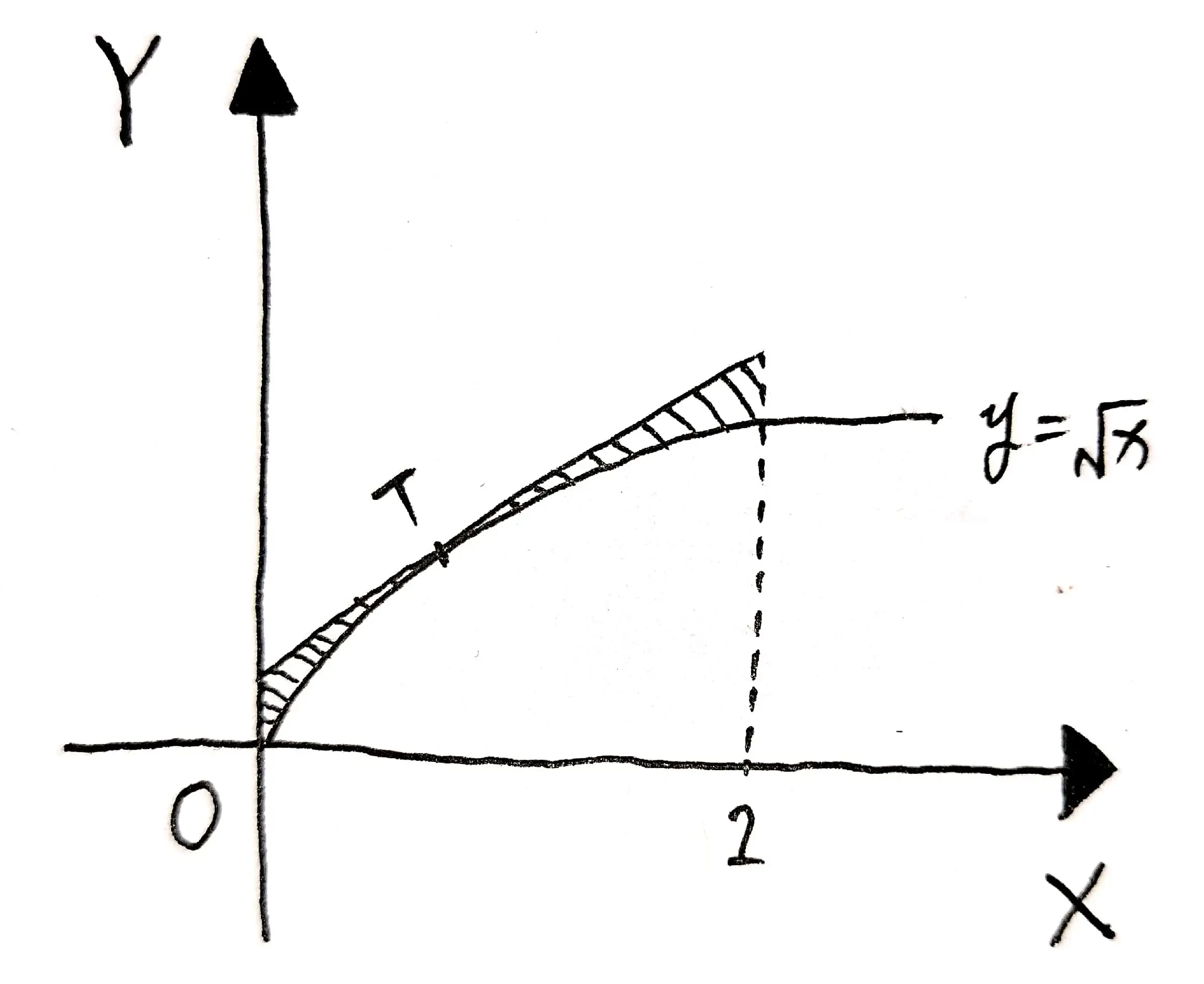
设切点为:
$$
T(t, \sqrt{t})
$$
则:
$$
y^{\prime}=\frac{1}{2 \sqrt{x}} \Rightarrow
$$
$$
y-\sqrt{t}=\frac{1}{2 \sqrt{t}}(x-t) \Rightarrow
$$
切线方程为:
$$
y=\frac{1}{2 \sqrt{t}} x+\frac{\sqrt{t}}{2}
$$
于是:
$$
S(t)=\int_{0}^{2}\left[\frac{1}{2 \sqrt{t}} x+\frac{\sqrt{t}}{2}-\sqrt{x}\right] \mathrm{~ d} x \Rightarrow
$$
$$
S(t)=\left.\frac{1}{4 \sqrt{t}} x^{2}\right|_{0} ^{2}+\left.\frac{\sqrt{t}}{2} x\right|_{0} ^{2}-\left.\frac{2}{3} x^{\frac{3}{2}}\right|_{0} ^{2} \Rightarrow
$$
$$
S(t)=\frac{1}{\sqrt{t}}+\sqrt{t}-\frac{4 \sqrt{2}}{3} \Rightarrow
$$
$$
S^{\prime}(t)=-\frac{1}{2} t^{\frac{-3}{2}}+\frac{1}{2} t^{\frac{-1}{2}} \Rightarrow
$$
$$
S^{\prime}(t)=0 \Rightarrow t=1
$$
又:
$$
S^{\prime \prime}(1)>0
$$
因此,要求解的切线方程为:
$$
y=\frac{1}{2} x+\frac{1}{2}
$$