四、解答题 (本题满分 12 分)
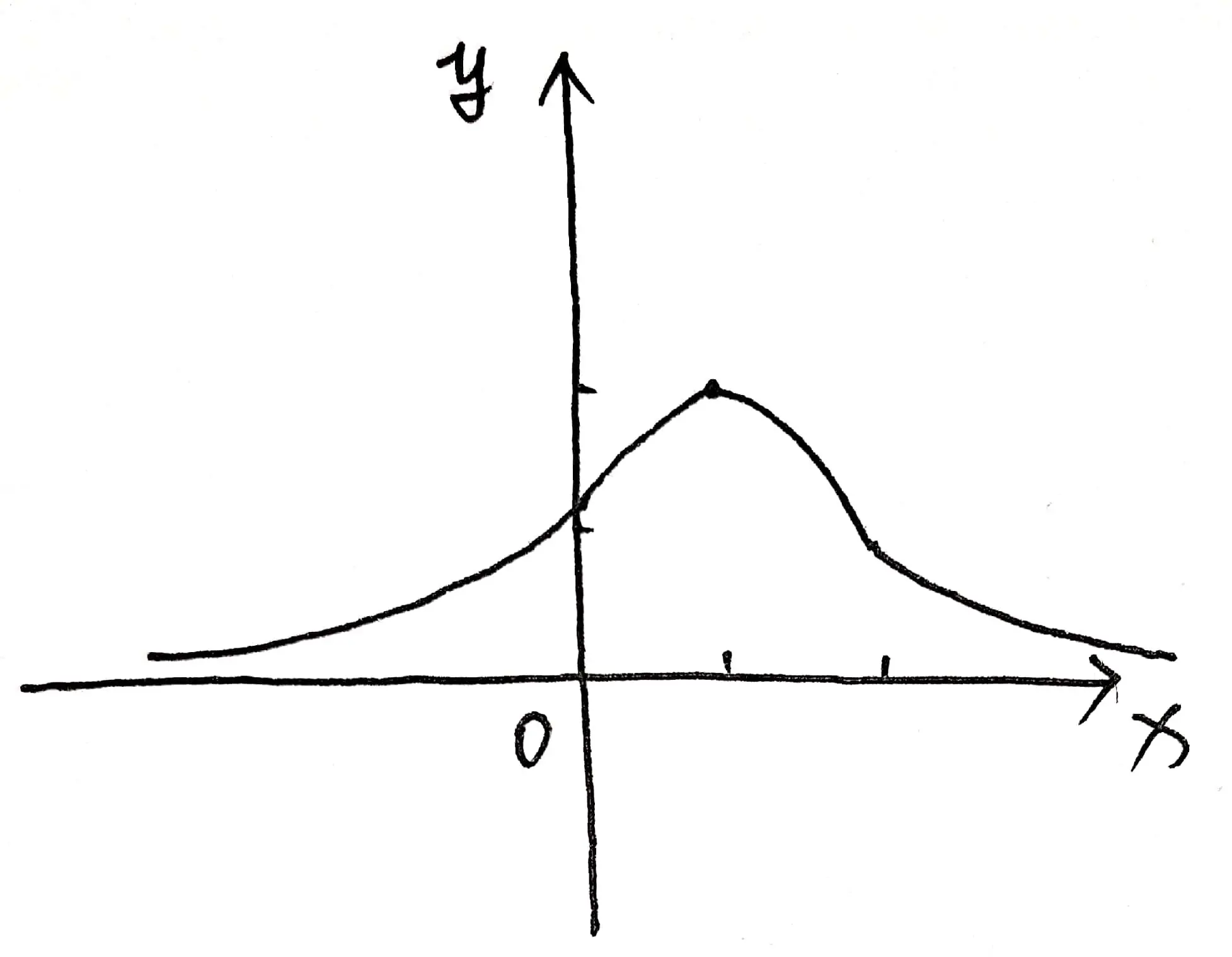
作函数 $y=\frac{6}{x^{2}-2 x+4}$ 的图形,并写出下面的内容:
- 单调增加区间
- 单调减少区间
- 极值点
- 极值
- 凹区间
- 凸区间
- 拐点
- 渐近线
$$
y=\frac{6}{x^{2}-2 x+4} \Rightarrow
$$
$$
y^{\prime}=\frac{-6(2 x-2)}{\left(x^{2}-2 x+4\right)^{2}}=\frac{12-12 x}{\left(x^{2}-2 x+4\right)^{2}}
$$
继续求导:
$$
y^{\prime \prime}=\frac{-12\left(x^{2}-2 x+4\right)^{2}-(12-12 x) \cdot 2\left(x^{2}-2 x+4\right) \cdot(2 x-2)}{\left(x^{2}-2 x+4\right)^{4}}
$$
$$
y^{\prime \prime}=\frac{-12\left(x^{2}-2 x+4\right)-2(2 x-2)(12-12 x)}{\left(x^{2}-2 x+4\right)^{3}}
$$
且 $x^{2}-2 x+4=(x-1)^{2}+3$ 恒大于零。
又:
$$
y^{\prime}=0 \Rightarrow 12-12 x=0\Rightarrow x=1
$$
因此唯一的极值为:
$$
y=\frac{6}{1-2+4}=2
$$
又:
$$
y^{\prime \prime}=0 \Rightarrow-12\left(x^{2}-2 x+4\right)-12(2 x-2)^{2}=0 \Rightarrow
$$
$$
36 x(x-2)=0 \Rightarrow
$$
$$
x=0 \text { 或者 } x=2
$$
因此,拐点为 $(0, \frac{3}{2})$ 和 $(2, \frac{3}{2})$.
而且,当 $x < 0$ 和 $x > 2$ 时,二阶导大于零,是凹区间,$x \in (0, 2)$ 时,二阶导小于零,是凸区间。
由于该函数没有间断点,因此没有垂直渐近线,又:
$$
\lim \limits_{x \rightarrow \pm \infty} \frac{6}{x^{2}-2 x+4}=\lim \limits_{x \rightarrow \pm \infty} \frac{6}{(x-1)^{2}+3}=0
$$
所以,该函数有一个水平渐近线为 $y = 0$.
综上可知:
- 单调增加区间:$(- \infty, 1)$
- 单调减少区间:$(1, + \infty)$
- 极值点:$x = 1$
- 极值:$y = 2$
- 凹区间:$x < 0$, $x > 2$
- 凸区间:(0, 2)
- 拐点:$(0, \frac{3}{2})$ 和 $(2, \frac{3}{2})$
- 渐近线:$y = 0$
该函数的示意图如图 03 所示: