二、选择题 (本题满分 20 分, 每小题 4 分)
(1) $f(x)=\frac{1}{3} x^{3}+\frac{1}{2} x^{2}+6 x+1$ 的图形在点 $(0,1)$ 处切线与 $x$ 轴交点坐标是
(A) $\left(-\frac{1}{6}, 0\right)$.
(B) $(-1,0)$.
(C) $\left(\frac{1}{6}, 0\right)$.
(D) $(1,0)$.
正确答案:A
$$
f^{\prime}(x)=x^{2}+x+6 \Rightarrow x=0 \Rightarrow k=6 \Rightarrow
$$
$$
y-1=6 x \Rightarrow y=6 x+1 \Rightarrow y=0, x=\frac{-1}{6} \Rightarrow
$$
$$
\left(-\frac{1}{6}, 0\right)
$$
(2) 设 $f(x)$ 与 $g(x)$ 在 $(-\infty,+\infty)$ 上皆可导, 且 $f(x) < g(x)$.
(A) $f(-x) > g(-x)$
(B) $f^{\prime}(x)<g^{\prime}(x)$.
(C) $\lim \limits_{x \rightarrow x_{0}} f(x)<\lim \limits_{x \rightarrow x_{0}} g(x)$.
(D) $\int_{0}^{x} f(t) \mathrm{d} t<\int_{0}^{x} g(t) \mathrm{d} t$.
正确答案:C
A 选项:如论写成 $-x$ 还是 $x$ 都只是一个符号,不会改变函数本身的性质,本项错误。
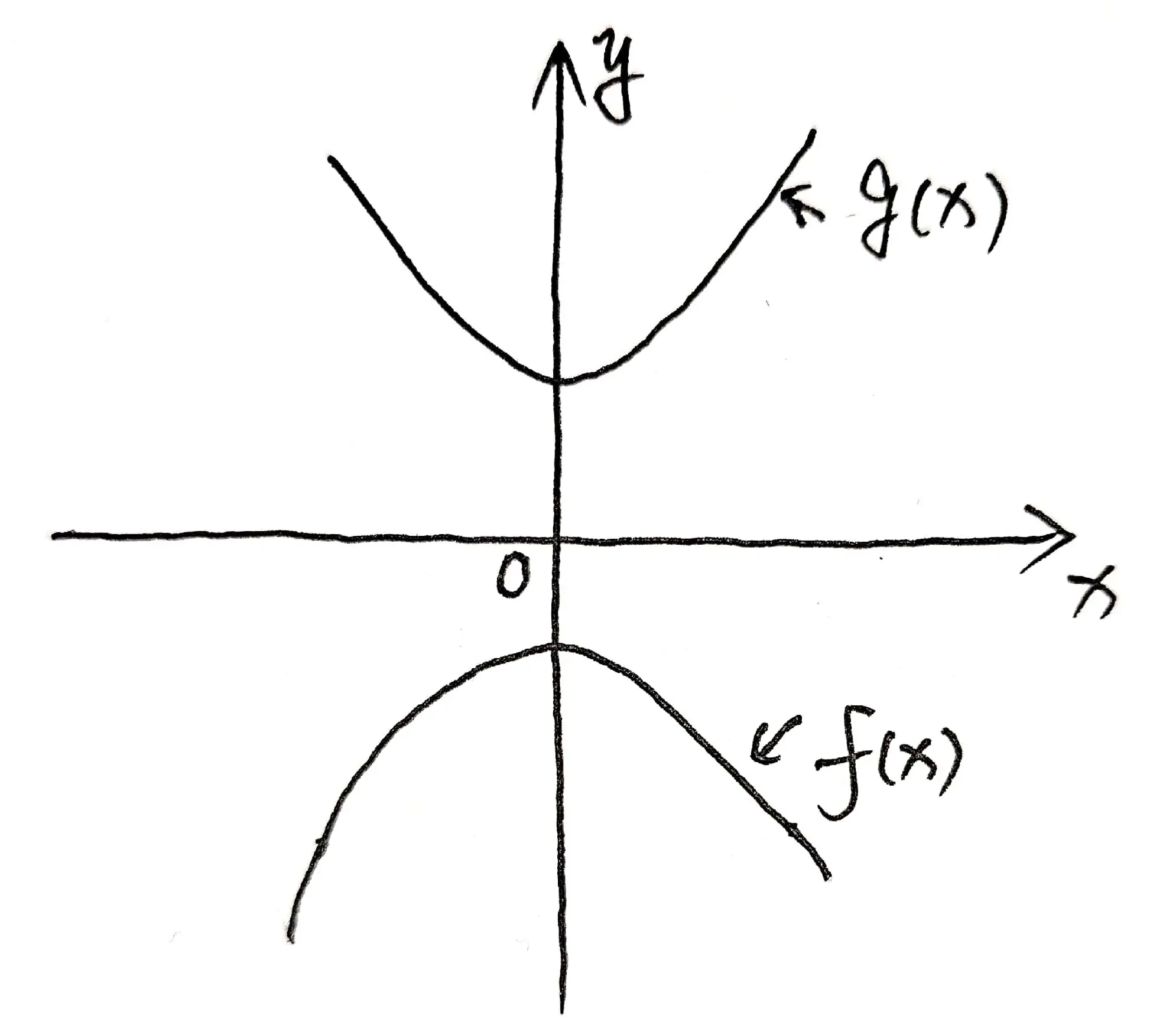
B 选项:如图 01 可知,本项错误:
C 选项:由于 $f(x) < g(x)$, 因此一定有 $f(x_{0}) < g(x_{0})$, 本想正确。
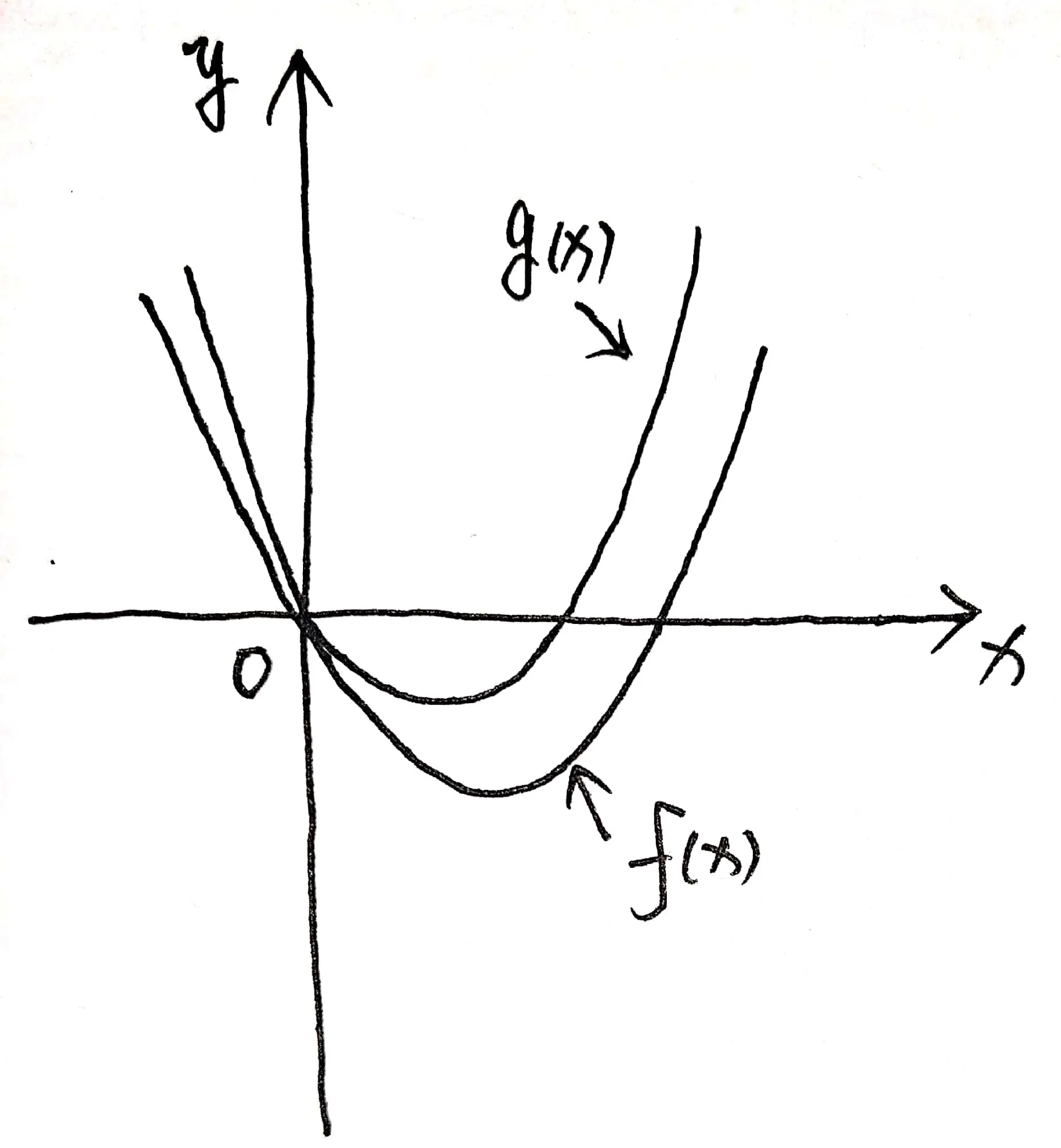
D 选项:由于负数的绝对值越大,负数本身就越小,因此,如果图 02 所示的情况可以说明 $\int_{0}^{x} f(t) \mathrm{d} t > \int_{0}^{x} g(t) \mathrm{d} t$
(3) 若函数 $y=f(x)$, 有 $f^{\prime}\left(x_{0}\right)=\frac{1}{2}$, 则当 $\Delta x \rightarrow 0$ 时, 该函数在 $x=x_{0}$ 处的微分 $\mathrm{d} y$
(A) 与 $\Delta x$ 是等价无穷小.
(B) 与 $\Delta x$ 是同阶无穷小.
(C) 是比 $\Delta x$ 低阶的无穷小.
(D) 是比 $\Delta x$ 高阶的无穷小.
正确答案:B
$$
\frac{d y}{\mathrm{~ d} x}=\frac{1}{2} \Rightarrow \frac{d y}{\Delta x}=\frac{1}{2} \Rightarrow \text { 同阶 }
$$
(4) 由曲线 $y=\sin ^{\frac{3}{2}} x(0 \leqslant x \leqslant \pi)$ 与 $x$ 轴围成的平面图形绕 $x$ 轴旋转而成的旋转体体积为
(A) $\frac{4}{3}$.
(B) $\frac{4}{3} \pi$.
(C) $\frac{2}{3} \pi^{2}$.
(D) $\frac{2}{3} \pi$.
正确答案:B
$$
V=\pi \int_{0}^{\pi}\left(\sin ^{\frac{3}{2}} x\right)^{2} \mathrm{~ d} x \Rightarrow
$$
$$
V=\pi \int_{0}^{\pi} \sin ^{3} x \mathrm{~ d} x=\pi \times 2 \times \int_{0}^{\frac{\pi}{2}} \sin ^{3} x \mathrm{~ d} x \Rightarrow
$$
$$
V=2 \pi \cdot \frac{2}{3} \cdot 1=\frac{4 \pi}{3}
$$
(5) 设函数 $y=f(x)$ 是微分方程 $y^{\prime \prime}-2 y^{\prime}+4 y=0$ 的一个解, 且 $f\left(x_{0}\right)>0, f^{\prime}\left(x_{0}\right)=0$, 则 $f(x)$ 在 $x_{0}$ 处
(A) 有极大值.
(B) 有极小值.
(C) 某邻域内单调增加.
(D) 某邻域内单调减少.
正确答案:A
注意:不要上来就去求解 $f(x)$, 在本题中,我们并不需要知道 $f(x)$ 具体是多少?
$$
y^{\prime \prime}-2 y^{\prime}+4 y=0 \Rightarrow
$$
$$
f^{\prime \prime}(x)-2 f^{\prime}(x)+4 f(x)=0 \Rightarrow
$$
$$
f^{\prime \prime}\left(x_{0}\right)-2 f^{\prime}\left(x_{0}\right)+4 f\left(x_{0}\right)=0 \Rightarrow
$$
$$
f^{\prime}\left(x_{0}\right)=0, f\left(x_{0}\right)>0 \Rightarrow
$$
$$
f^{\prime \prime}\left(x_{0}\right)=-4 f\left(x_{0}\right)<0
$$