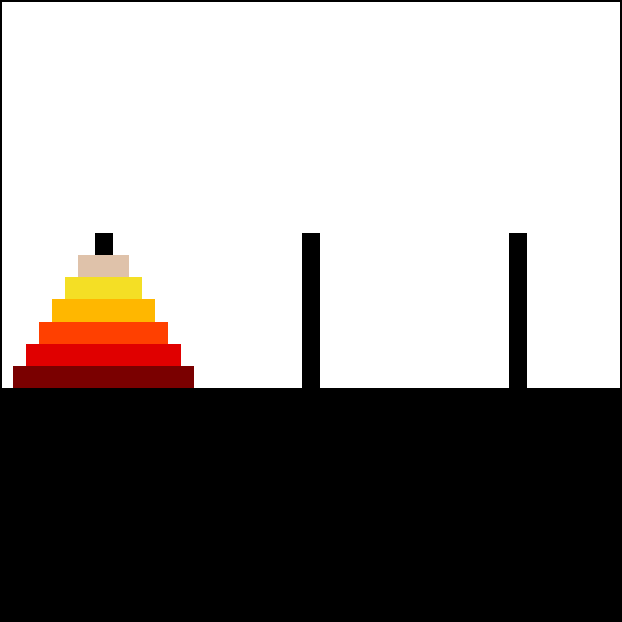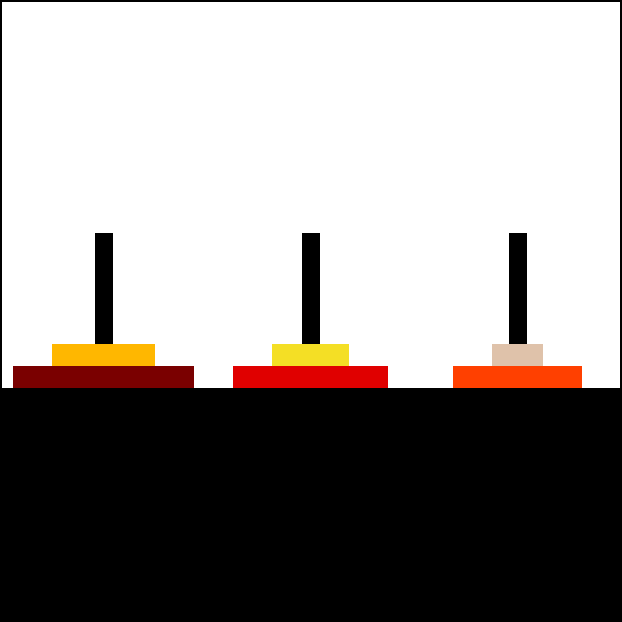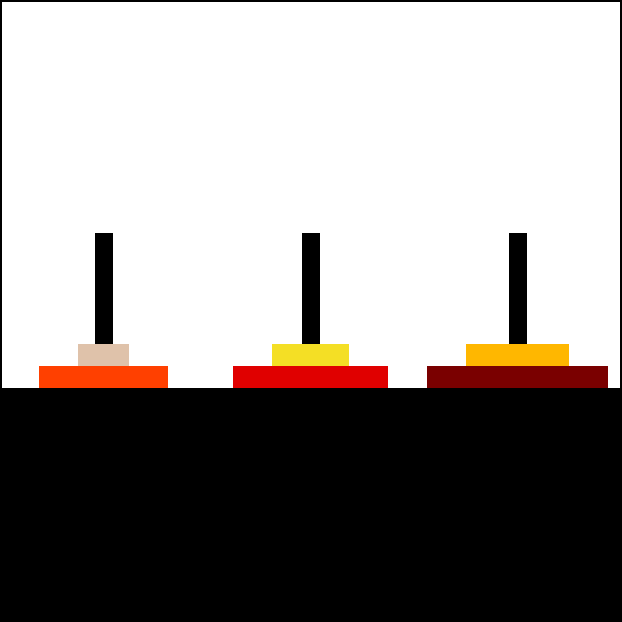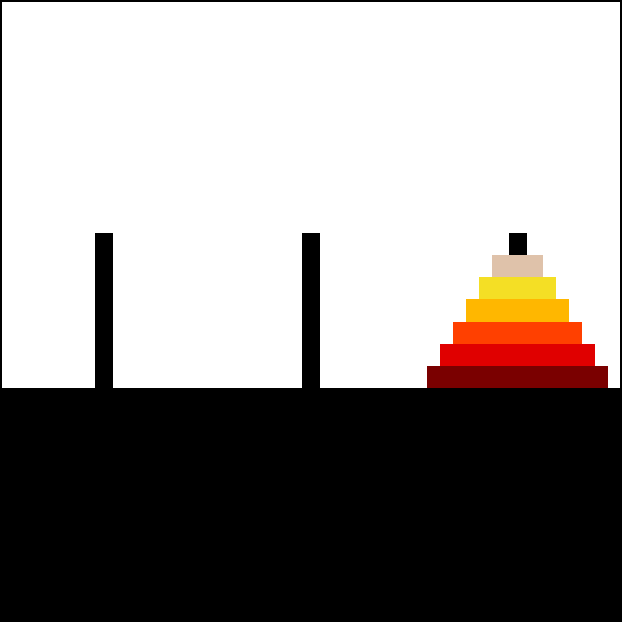递归 (一): 递归思想与 C++ 中的递归函数及两个递归应用示例 (斐波那契, 汉诺塔)

什么是递归

从汇编层面上看递归

在汇编层面上, 递归可以看作是两个循环, 每个循环的循环参数都由另一个循环传入

从算法思想上看递归

递归是基于分治的, 也就是”分而治之”. 当需要求解的问题的输入规模为 N, 而 N 又很大的时候, 直接按照线性过程求解将十分困难. 这个时候, 如果 N 具有某些特性, 能够被分解成更小规模的问题 n, 并且这些小规模的问题 n 满足以下条件:

由全部 n 的解能够得出 N 的解;
全部 n 之间互相独立, n 与 n 之间不存在公共区域.
这时, 我们就可以考虑使用”分支”来对 N 进行求解. 如果求解小规模问题 n 的方法和求解大规模问题 N 的方法是一致的 (n 具有 N 的最优子结构性质), 那么这时候就可以考虑更进一步地使用递归的思想求解.

从高级程序语言形式上看递归

在高级语言中, 递归的表现形式就是一个函数直接或间接地调用了自己, 直到满足出口条件, 结束递归.

从语义上看递归

“递归”分开就是”递”和”归”, “递”是离开自己, “归”是回到自己. 中文中的”递归”一词也表明了递归函数是一个来回往复的运算过程. 在英文中, “递归”的英文是”recursion”, “recursion”包含”重复”的意思. 另外, “递归”与”循环”在语义上也有明显的区别, “递归 (recursion)”是一个一维的往复结构, 而”循环 (loop)”则是一个二维的环状结构.

C++ 中的递归函数示例

斐波那契数列 (Fibonacci sequence)

斐波那契数列来源于斐波那契在其著作《计算之术》中提出的一个问题:

在第一个月有一对刚出生的小兔子，在第二个月小兔子变成大兔子并开始怀孕，第三个月大兔子会生下一对小兔子，并且以后每个月都会生下一对小兔子。如果每对兔子都经历这样的出生、成熟、生育的过程，并且兔子永远不死，那么兔子的总数是如何变化的？
斐波那契《计算之术》

对于上面这个问题我们可以得出这样一个过程:

第 01 个月: 01 只小兔子 –> 01

第 02 个月: 01 只大兔子 –> 01

第 03 个月: 01 只大兔子 + 01 只小兔子 –> 02

第 04 个月: 02 只大兔子 + 01 只小兔子 –> 03

第 05 个月: 03 只大兔子 + 02 只小兔子 –> 05

第 06 个月: 05 只大兔子 + 03 只小兔子 –> 08

第 07 个月: 08 只大兔子 + 05 只小兔子 –> 13

…

于是, 我们得到了这样一个数列:

1,1,2,3,5,8,13,21,34…

这就是斐波那契数列 (也叫”兔子数列”).

我们先来借助 for 循环, 使用迭代来计算前 30 位斐波那契数列, 程序如下:

#include<stdio.h>
#include<bits/stdc++.h>
using namespace std;
#define MAX_SIZE 30
int main(){
    int a[MAX_SIZE];
    a[0]=0;
    a[1]=1;
    printf("%d ",a[1]);

    for(int i=2;i<=MAX_SIZE;i++){
        a[i]=a[i-1]+a[i-2];
        printf("%d ",a[i]);
    }
    return 0;
}

运行结果:

1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181 6765 10946 17711 28657 46368 75025 121393 196418 317811 514229

迭代实现的求解斐波那契数列很好理解, 下面使用递归来实现一下.

下面的程序可以计算斐波那契数列中指定位置的值, 程序如下:

#include<stdio.h>
#include<bits/stdc++.h>

using namespace std;

int f(int n){
    if(n==0){
        return 1;
//斐波那契数列的首位是 1, 因此返回 1 
    }else if(n==1){
        return 1;
//斐波那契数列的第 2 位是 1, 因此返回 1 

    }else{
        return f(n-1)+f(n-2);
//从斐波那契数列的第 3 位及以后开始都可以使用前面两位的和计算出 
    }   
}

int main(){
    int a=f(7); //返回斐波那契数列的第 7 个值(从 0 开始计算) 
    printf("%d\n",a);
    system("pause");
    return 0;
}

为了搞清楚递归的函数调用过程, 我们对上面的程序设置两个断点, 之后采用”单步进入”的方式逐步观察计算过程, 为了方便说明, 我们将函数 f() 的参数设置为 5, 即:

int a=f(5);

断点设置情况如下:

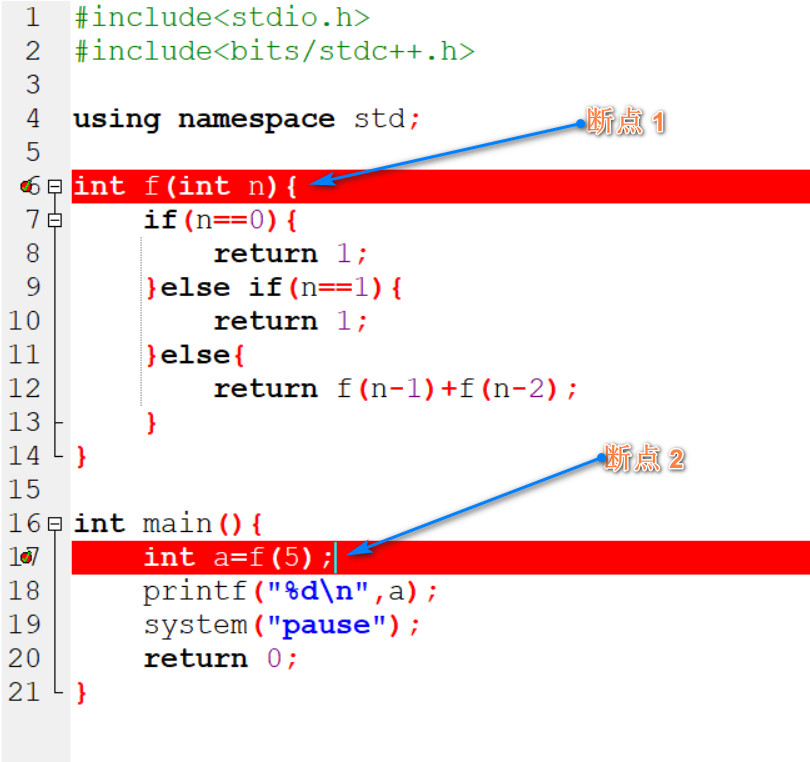
下面开始逐步分析展示本次调试过程:

01: a 为一个随机的初始值 31.

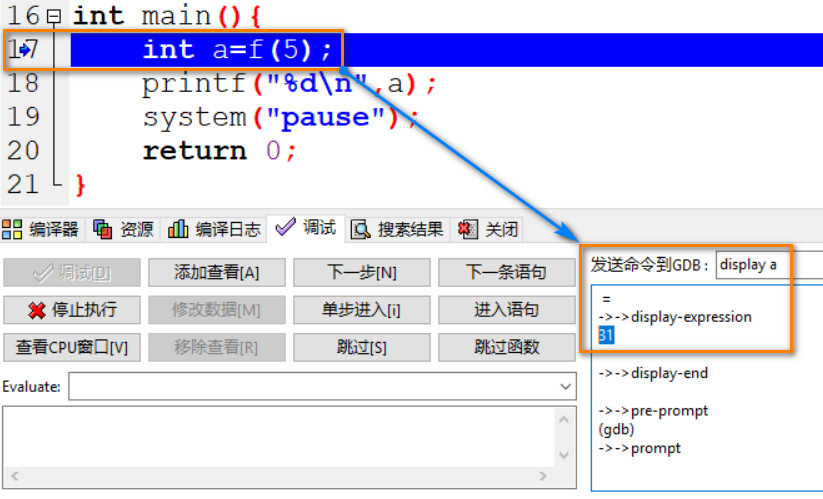
02: 参数 5 被传递给函数 f(n), n=5.

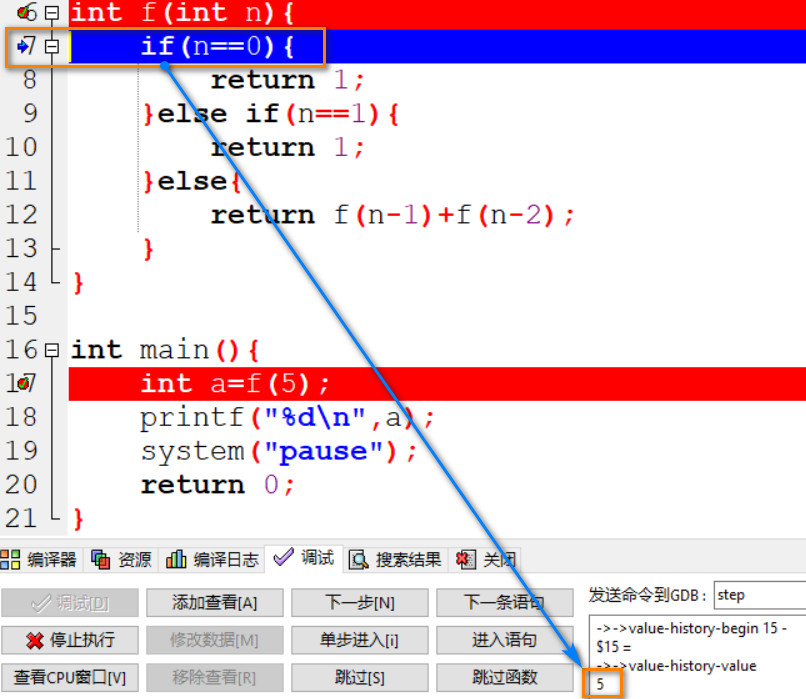
03: n 进入 else if 语句并和 1 对比判断是否相等, 此时 n=5.

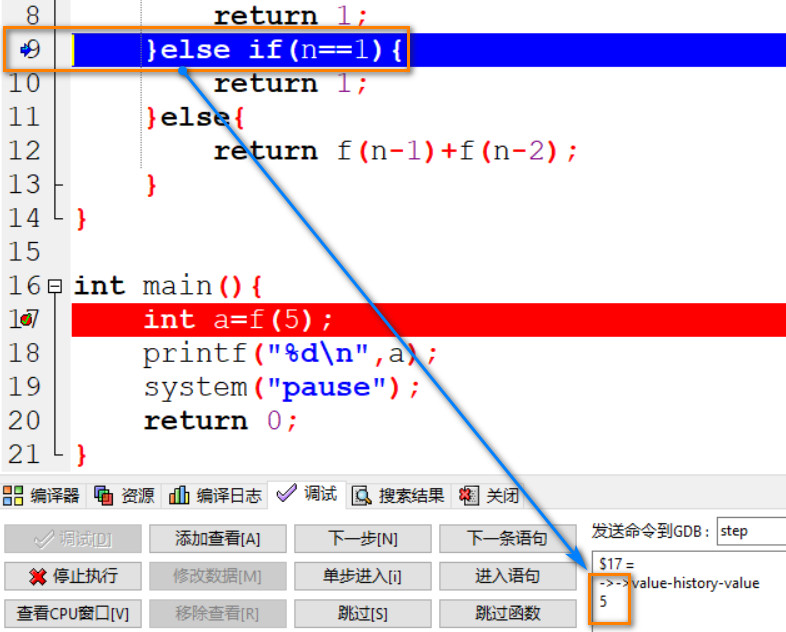
04: 由于 5!=1, n 进入 else 语句, 此时 return f(5-1)+f(5-2);

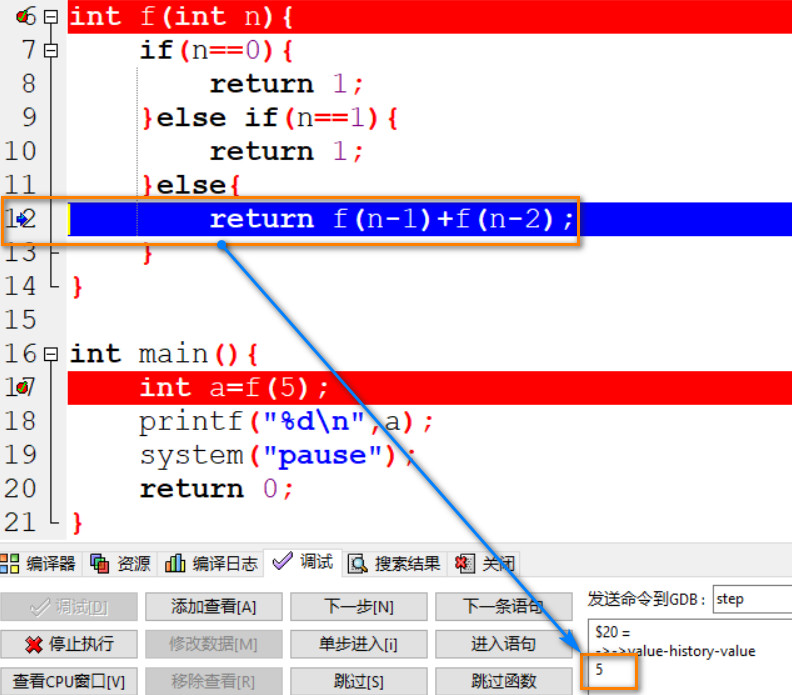
05: 由于不知道上一步需要的 f(4) 和 f(3) 的值, 因此 n-1=4 并重新执行 f(n) 函数, 此时 n=4.

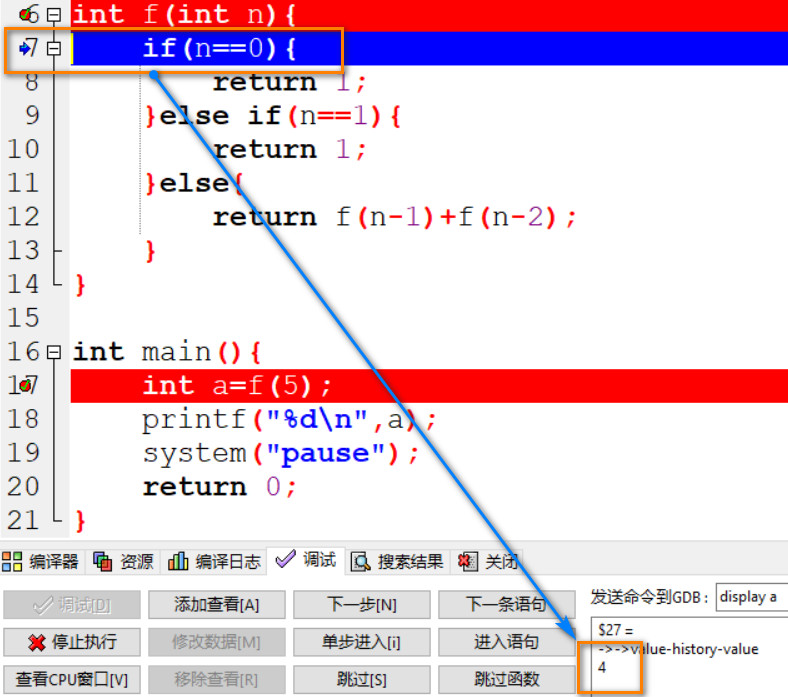
06: n 进入 else if 语句并和 1 对比判断是否相等, 此时 n=4.

07: 由于 4!=1, n 进入 else 语句, 此时 return f(4-1)+f(4-2);

08: 由于不知道上一步需要的 f(3) 和 f(2) 的值, 因此 n-1=3 并重新执行 f(n) 函数, 此时 n=3.

09: n 进入 else if 语句并和 1 对比判断是否相等, 此时 n=3.

10: 由于 3!=1, n 进入 else 语句, 此时 return f(3-1)+f(3-2);

11: 由于不知道上一步需要的 f(2) 和 f(1) 的值, 因此 n-1=2 并重新执行 f(n) 函数, 此时 n=2.

12: n 进入 else if 语句并和 1 对比判断是否相等, 此时 n=2.

13: 由于 2!=1, n 进入 else 语句, 此时 return f(2-1)+f(2-2);

14: 由于不知道上一步需要的 f(1) 和 f(0) 的值, 因此 n-1=1 并重新执行 f(n) 函数, 此时 n=1.

15: n 进入 else if 语句并和 1 对比判断是否相等, 此时 n=1, 由于 1=1 为真, 因此返回 1 并跳出 if 判断语句:

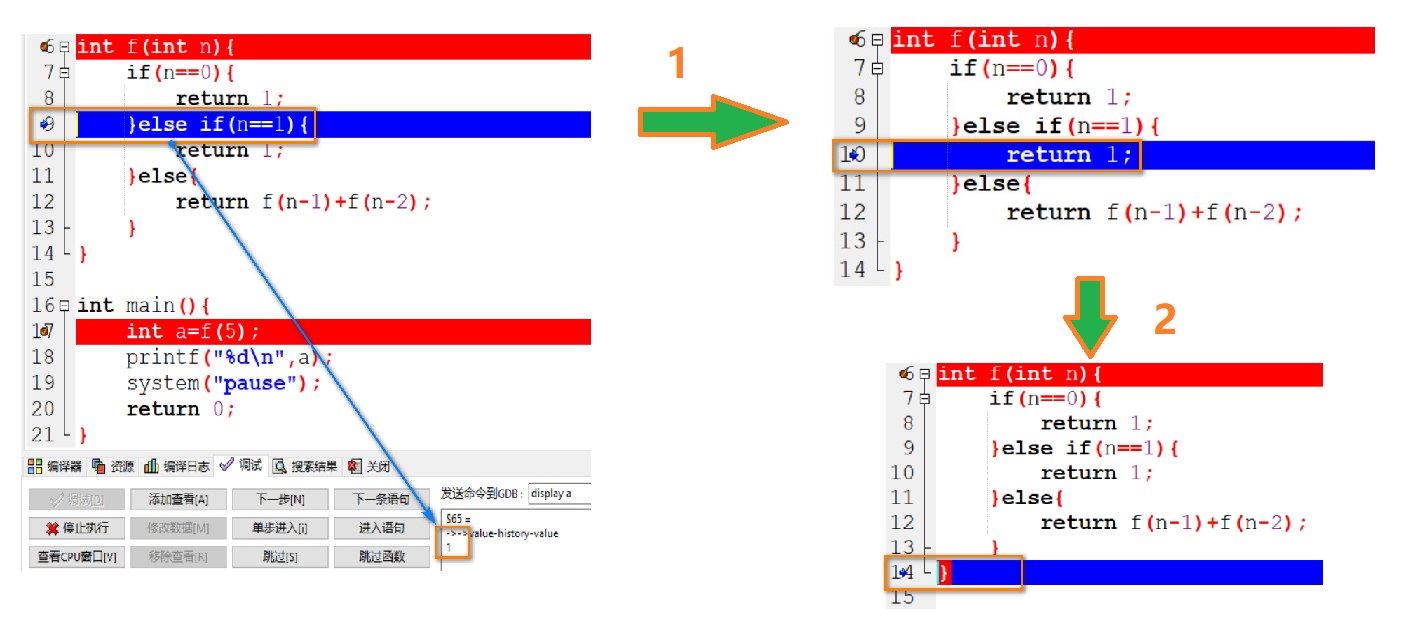
16: 经过上面的步骤知道了 f(1) 的值, 但是还不知道 f(0) 的值, 因此 n-1=1 并重新执行 f(n) 函数, 此时 n=0. 由于 0=0 为真, 因此返回 1, 至此, 边界条件 f(0) 和 f(1) 的值都知道了.

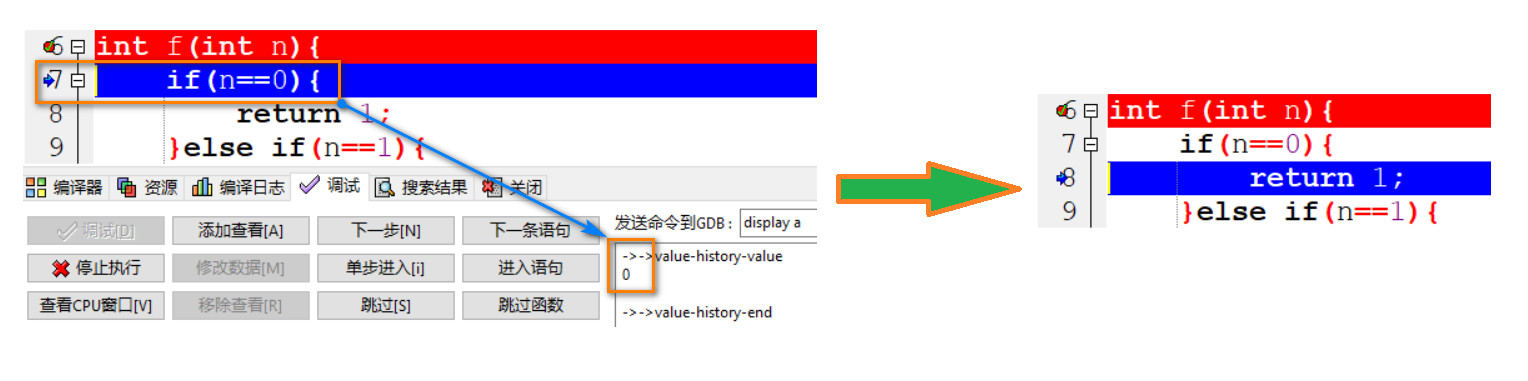
(后续过程不再使用文字描述, 见下面的图片说明.)

这个过程其实就是一个二叉树的遍历过程, 我用图片的形式绘制了整个过程, 如图 9:

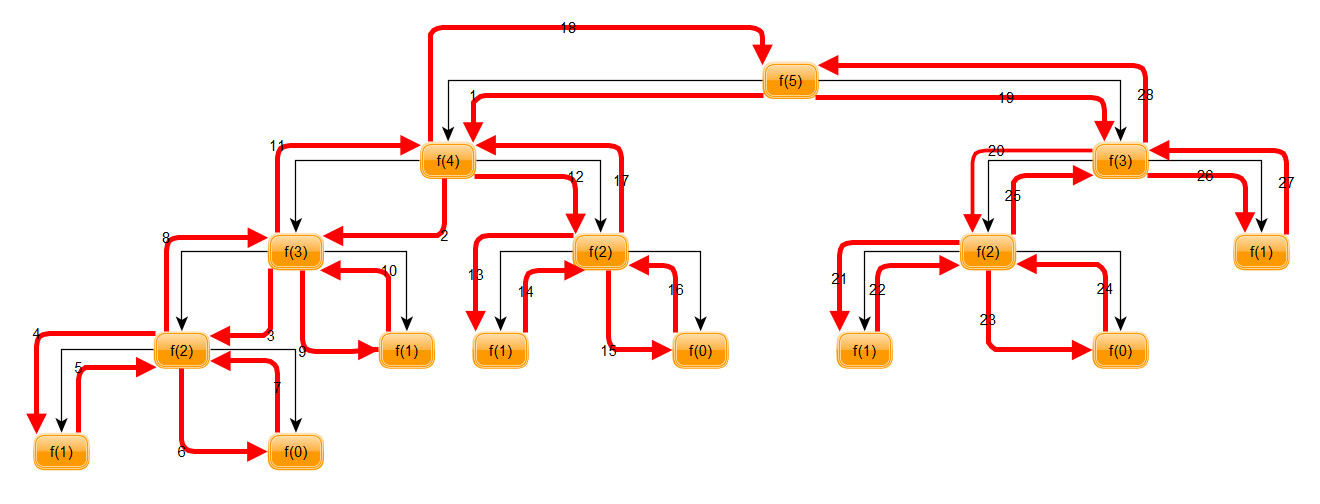
上面这个程序运行一次只能输出斐波那契数列中的一个数值, 下面对该程序进行一个改进, 使得可以输出指定的前 n 位的斐波那契数列, 程序如下:

#include<stdio.h>
#include<bits/stdc++.h>
using namespace std;

int f(int n){
    if(n==0){
        return 1;
    }else if(n==1){
        return 1;
    }else{
        return f(n-1)+f(n-2);
    }   
}


int main(){
    int n=5; //设置打印前 6 个斐波那契数列元素 
    for(int i=0;i<=n;i++){
        int a=f(i);
        printf("%d ",a);
    }
    system("pause");
    return 0;
}

上述程序的运行结果是:

1 1 2 3 5 8

汉诺塔 (Tower of Hanoi)

Wikipedia 上对于汉诺塔问题的说明如下:

The Tower of Hanoi (also called the Tower of Brahma or Lucas’ Tower and sometimes pluralized) is a mathematical game or puzzle. It consists of three rods and a number of disks of different sizes, which can slide onto any rod. The puzzle starts with the disks in a neat stack in ascending order of size on one rod, the smallest at the top, thus making a conical shape.
The objective of the puzzle is to move the entire stack to another rod, obeying the following simple rules:
1. Only one disk can be moved at a time.
2. Each move consists of taking the upper disk from one of the stacks and placing it on top of another stack or on an empty rod.
3. No larger disk may be placed on top of a smaller disk.
With 3 disks, the puzzle can be solved in 7 moves. The minimal number of moves required to solve a Tower of Hanoi puzzle is 2n − 1, where n is the number of disks.
Wikipedia, Source: https://en.wikipedia.org/wiki/Tower_of_Hanoi

原始的汉诺塔问题是一个来自于印度的数学游戏, 在该游戏中, 有三根柱子, 其中一根柱子上有 64 个圆盘, 且这些圆盘都按照较大的圆盘在较小的圆盘下面的原则放置, 如图 10:

图 10 图片来自 Wikipedia, Source: https://commons.wikimedia.org/wiki/File:Tower_of_Hanoi.jpeg

现在要把这些圆盘从目前的柱子上移动到另外两根柱子的其中一根上, 要求如下:

一次只能移动一个圆盘.
大圆盘必须始终在小圆盘的下面.

汉诺塔问题十分适合使用递归来解决, 使用”分治”的思想来思考这个问题就能找到解决问题的思路. 我们首先考虑如果这个汉诺塔问题只有两个圆盘时该如何移动圆盘(假设三个柱子从左向右依次为 A, B, C):

把 A 上较小的圆盘放到 B 上
把 A 上较大的圆盘放到 C 上
把 B 上较小的圆盘放到 C 上

通过这三步, 将 B 柱作为一个中转柱, 我们就完成了把 A 上的圆盘全部转移到 C 上任务, 整个过程都符合汉诺塔的游戏规则.

但是, 我们现在有 64 个圆盘, 不是 2 个圆盘, 这该怎么办呢? 我们这时可以用”分治”的思想来想想看. 如图 11, 我们把 A 柱上较小的 63 个圆盘看作一个圆盘, 把下面最大的那个圆盘看作 1 个圆盘, 这样就成了”两个圆盘”, 因此可以使用上面关于只有两个圆盘时的移动方式来解决这个问题, 过程都显示在下面的图片里了:

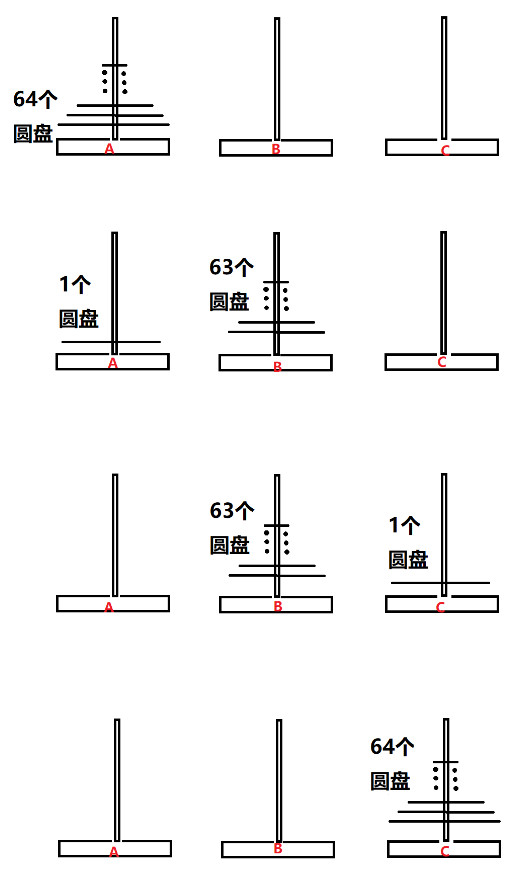
那么之后该怎么做呢?

当我们把最大的一个圆盘移动到 C 上, 把 63 个较小的圆盘移动到 B 上之后, 即图 11 中的第 3 步, 我们可以发现, 此时圆盘的分布和图 11 中的第 2 步是很相似的, 只不过空出来的柱子由 C 变成了 A, 于是, 就有了下面这个过程:

把 A 柱上的前 63 个圆盘移动到 B 柱 (此时 B 柱作为中转);
把 A 柱上的第 64 个圆盘移动到 C 柱;
把 B 柱上的前 62 个圆盘移动到 A 柱 (此时 A 柱作为中转);
把 B 柱上的第 63 个圆盘移动到 C 柱;
把 A 柱上的前 61 个圆盘移动到 B 柱 (此时 B 柱作为中转);;
把 A 柱上的第 62 个圆盘移动到 C 柱;
…

将多个圆盘看作是一个圆盘与真的是一个圆盘其实是一样的. 下面我们从递归的程序角度思考一下这个过程:

如果要移动第 64 个, 必须先移动完前 63 个;
如果要移动第 63 个, 必须先移动完前 62 个;
如果要移动第 62 个, 必须先移动完前 61 个;
(…省略若干行…)
如果要移动第 2 个, 必须先移动完第 1 个;
第 1 个是可以自由移动的, 于是, 我们把第 1 个移动到 B 柱(由于不是只有 1 个圆盘, 因此第 1 个圆盘要去中转柱而不是最终的目标柱);
现在可以把第 2 个移动到 C 柱了;
但是 A 柱上的圆盘并没有被移动完, 为了能移动完, 我们现在必须想办法让第 3 个圆盘到 C 柱(之后以此类推可以让第 4,5,6…64个圆盘到 C 柱);
于是, 我们把第 1 个圆盘从 B 柱移动到 A 柱, 把第 2 个圆盘从 C 柱移动到 B 柱, 把第 1 个圆盘从 A 柱移动到 B 柱, 把第 3 个圆盘从 A 柱移动到 C 柱.
好啦, 现在第 3 个圆盘成功的到了 C 柱.
不过还没完, 我们需要重复上面的过程, 直到把第 64 个圆盘移动到 C 柱, 之后, 第 64 个圆盘在之后的移动过程中就可以不用动了, 一直待在 C 柱上.
对于剩下的 63 个圆盘重复和原来 64 个圆盘一样的移动过程即可.

这么移动的工作量是很大的, 移动完全部 64 个圆盘需要大约 1800 亿亿步:

18,446,744,073,709,551,615

根据上面的介绍, 用 C++ 实现的话, 程序是这样的:

#include<iostream>
#include<bits/stdc++.h>
using namespace std;

//假设函数 (int n, char a, char b, char c) 的作用是将 n 个圆盘从 a 移动到 c 

void f(int n, char a, char b, char c){
        if(n==1){
            cout<<"将盘子"<<n<<"从"<<a<<"移动到"<<c<<endl;
    //当只有 1 个盘子时, 直接从 a 移动到 c 
        }else{
            f(n-1,a,c,b);
    //将 n-1 个圆盘由 a 移动到 b 
            cout<<"将盘子"<<n<<"从"<<a<<"移动到"<<c<<endl;
            f(n-1,b,a,c);
    //将 n-1 个圆盘由 b 移动到 c 
        }
    }

int main(){
    f(3,'a','b','c');                                                                                                                                                                                                                                                                                                    
    return 0;
}

上面这个程序的运行结果如下 (圆盘的序号越大则圆盘越大):

假设有三个圆盘, 移动顺序是这样的:

将盘子1从a移动到c
将盘子2从a移动到b
将盘子1从c移动到b
将盘子3从a移动到c
将盘子1从b移动到a
将盘子2从b移动到c
将盘子1从a移动到c

假设有四个圆盘, 移动顺序是这样的:

将盘子1从a移动到b
将盘子2从a移动到c
将盘子1从b移动到c
将盘子3从a移动到b
将盘子1从c移动到a
将盘子2从c移动到b
将盘子1从a移动到b
将盘子4从a移动到c
将盘子1从b移动到c
将盘子2从b移动到a
将盘子1从c移动到a
将盘子3从b移动到c
将盘子1从a移动到b
将盘子1从a移动到b
将盘子2从a移动到c
将盘子1从b移动到c

最后, 来看几个关于汉诺塔问题的动图吧.

图 12:

图 12 By André Karwath aka Aka – Own work, CC BY-SA 2.5, https://commons.wikimedia.org/w/index.php?curid=85401

图 13: