前言
本文将对摆线做一个介绍并列举一些摆线的基本性质。
Note
摆线是数学一、数学二、数学三都可能考察的知识点。
zhaokaifeng.com
正文
什么是摆线
在数学上,摆线指的是一个圆沿着一条直线滚动时,圆边界上一个固定的点所形成的轨迹,如图 1 所示的这条红线即为摆线:

由Zorgit – 自己的作品,CC BY-SA 3.0,https://commons.wikimedia.org/w/index.php?curid=4552689
摆线的基本性质
一个半径为 $r$ 的圆所形成的过平面直角坐标原点的摆线的参数方程为:
$$
\left\{\begin{matrix}
x = r(t – \sin t);\\
y = r(1 – \cos t).
\end{matrix}\right.
$$
上面的参数 $t$ 是该圆滚动过的角度,当圆滚动一周 ($t = 0 \rightarrow 2 \pi$) 就会形成一个完整的“拱”。这个完整的“拱”有如下性质:
一、拱的跨度为 $2 \pi r$ (一个圆转了 360 度之后刚好转完一周,因此,这个圆“行走的轨迹”的长度,同时也是拱的跨度,刚好是圆的周长).
二、拱的长度为 $8r$ (圆直径的 $4$ 倍).
三、拱和坐标轴所围成图形的面积为 $3 \pi r^{2}$ (圆面积的 $3$ 倍).
四、拱的高度为 $2r$ (一个拱的最高点的高度就是元的直径).
例如图 2 所示,这是一个由半径为 $2$ 的圆所生成的摆线,从图中可以看到该摆线的两个完整的拱:
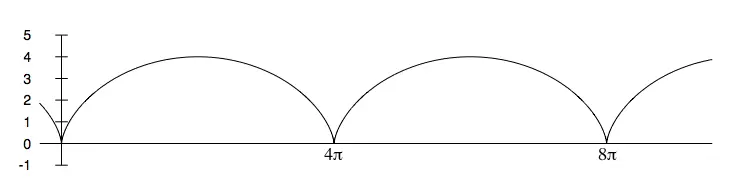
由Doctormatt – 自己的作品,公有领域,https://commons.wikimedia.org/w/index.php?curid=2193340
References:
[1]. 摆线 – 维基百科,自由的百科全书
https://zh.wikipedia.org/wiki/摆线
EOF