冒泡排序算法的排序过程
(以下排序过程按照大数位于小数右边的规则展开说明,按照大数位于小数左边的规则进行的冒泡排序与此过程类似)
- 首先进行第 1 次遍历,选取整个队列 (队列长度为 N) 的第 1 个数字 (记为 a),和紧邻 a 后的数字 (记为 b) 比较大小,如果 a 大于 b, 则交换 a 与 b 的位置,此后,a 继续和紧邻 a 后的数字 c 比较;如果 a 小于 b, 则丢下 a, 拿起 b, 并和紧邻 b 后的后的数字比较大小。经过这一轮比较,当比较到整个队列结束时,一共进行了 N-1 次比较,此时,整个队列中最大的数字排在了整个队列的最后;
- 现在进行第 2 次遍历,此时只需要遍历除了第 1 次遍历后得到的数列的最后一个数之外的 N-1 个数字,即需要比较 N-2 次,得到整个数列第 2 大的数字排在上一轮排序得到的最大的数字的左边;
- 依照前面两步所示的规则继续进行第 3, 4, 5, …, N-1 轮循环就完成了整个排序过程。
以数列 [3,2,5,1,2] 为例,冒泡排序的过程如下:
第 1 轮第 1 次比较:[2,3,5,1,2];
第 1 轮第 2 次比较:[2,3,5,1,2];
第 1 轮第 3 次比较:[2,3,1,5,2];
第 1 轮结束:[3,2,1,2,5];
第 2 轮结束:[2,1,2,3,5];
第 3 轮结束:[1,2,2,3,5];
第 4 轮结束:[1,2,2,3,5].
下面这个动图很好的演示了冒泡排序的整个过程:
(该动图使用 VisuAlgo 制作,来自:https://visualgo.net/)
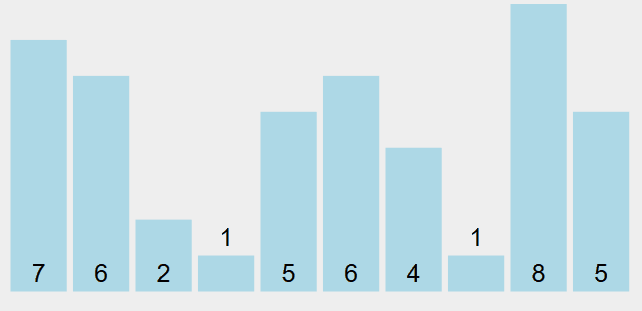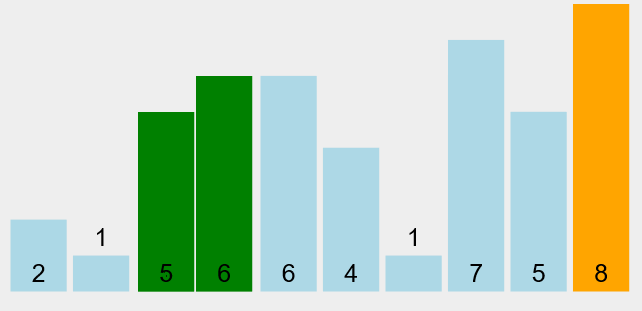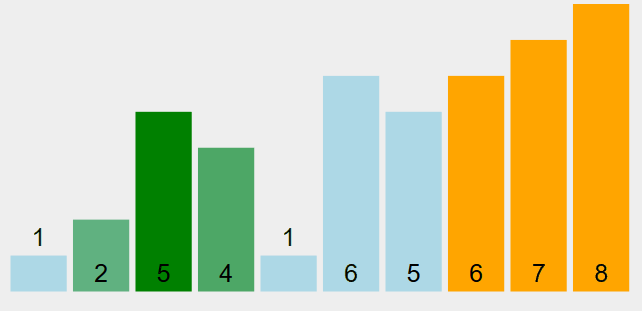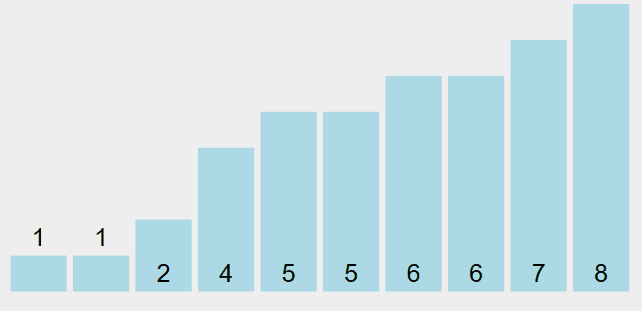
C++ 实现的冒泡排序算法
递归实现
#include <iostream>
using namespace std;
int * mp(int a[], int start, int end){
if(start<end){
/*
使用start和end这两个变量定义递归的边界条件,
start表示数组的起始位置,end表示数组的结束
位置,每次循环结束时,end都会减1,因此当start
不再小于end的时候,就代表整个数组都被遍历了,
即递归操作完成。
*/
int temp = 0;
for(int i = 0; i <= 8; i++){
if(a[i]>a[i+1]){
temp = a[i];
a[i] = a[i+1];
a[i+1] = temp;
}
}
end --;
mp(a,start,end);
}
return a;
}
int main(){
int start = 0;
int end = 9;
int a[10] = {7,6,2,1,5,6,4,0,8,5};
int *p;
p = mp(a,start,end);
for(int j = 0; j <=8; j++){
cout << *(p+j) << " ";
}
return 0;
}
运行后输出的结果:
0 1 2 4 5 5 6 6 7 Process returned 0 (0x0) execution time : 0.085 s Press any key to continue.
非递归实现
双层 for 循环实现的冒泡排序(无改进)
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
int main(){
int nums[10]={7,6,2,1,5,6,4,0,8,5};
int temp=0;
for(int i=0;i<=8;i++){
/*有10个数字的队列首次遍历需要比较9次,之后,
每次遍历需要比较的数字的个数都比上一次少1个。
这层循环用于确定需要遍历的队列的长度。*/
for(int j=0;j<8-i;j++){
/*从队列第 1 个数字开始,比较到不需要比较的最后
一个数字为止,这层循环用于确定需要比较的具体的
数字。*/
if(nums[j]>nums[j+1]){
/*如果前一个数大于后一个数,则交换两个数的位置,
把大的数字放到后面。*/
temp = nums[j+1];
nums[j+1]= nums[j];
nums[j] = temp;
}
}
}
for(int z=0;z<=8;z++){
cout<<nums[z]<<" ";
}
return 0;
}
上面这个程序的时间复杂度为:O(n^2^), 空间复杂度为:O(1).
双层 for 循环实现的冒泡排序(使用位置交换标志位进行改进)
我们首先对上面“双层 for 循环实现的冒泡排序(无改进)”中给出的程序做一些改变,使其能打印出每一轮排序的结果,程序如下:
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
int main(){
int nums[10]={7,6,2,1,5,6,4,0,8,5};
int temp=0;
for(int i=0;i<=8;i++){
for(int j=0;j<8-i;j++){
if(nums[j]>nums[j+1]){
temp = nums[j+1];
nums[j+1]= nums[j];
nums[j] = temp;
}
}
cout<<i<<"#:"<<" ";
for(int z=0;z<=8;z++){
cout<<nums[z]<<" ";
}
cout<<endl;
}
return 0;
}
运行上面的程序后可以得到如下结果:
0#: 6 2 1 5 6 4 0 7 8 1#: 2 1 5 6 4 0 6 7 8 2#: 1 2 5 4 0 6 6 7 8 3#: 1 2 4 0 5 6 6 7 8 4#: 1 2 0 4 5 6 6 7 8 5#: 1 0 2 4 5 6 6 7 8 6#: 0 1 2 4 5 6 6 7 8 7#: 0 1 2 4 5 6 6 7 8 8#: 0 1 2 4 5 6 6 7 8 Process returned 0 (0x0) execution time : 0.267 s Press any key to continue.
通过上面的运行结果可以看出第 6 轮循环结束时排序其实已经完成,之后的 7, 8 轮排序得出的结果和第 6 轮排序得出的结果完全一致。我们可以通过在程序中添加“位置交换标志位”来避免无用的排序,即一旦发现某一轮循环结束之后没有任何一个元素的位置发生了改变,就认为此时排序已经完成,不需要进行接下来的排序。
使用“位置交换标志位”改进后的程序如下:
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
int main(){
int nums[10]={7,6,2,1,5,6,4,0,8,5};
int temp=0;
bool SwapFlag = true;
/*
定义位置交换标志变量
当发生位置交换时置为 true
未发生位置交换时置为 false
*/
for(int i=0;i<=8&&SwapFlag==true;i++){
SwapFlag=false;
/*
每开始一轮排序时都将标志位复位
(初始默认本轮不会出现交换)
*/
for(int j=0;j<8-i;j++){
if(nums[j]>nums[j+1]){
SwapFlag=true;
/*
只要在一轮排序中发生了一次交换
则标志位置为 true
*/
temp = nums[j+1];
nums[j+1]= nums[j];
nums[j] = temp;
}
}
cout<<i<<"#:"<<" ";
for(int z=0;z<=8;z++){
cout<<nums[z]<<" ";
}
cout<<endl;
}
return 0;
}
输出结果如下:
0#: 6 2 1 5 6 4 0 7 8 1#: 2 1 5 6 4 0 6 7 8 2#: 1 2 5 4 0 6 6 7 8 3#: 1 2 4 0 5 6 6 7 8 4#: 1 2 0 4 5 6 6 7 8 5#: 1 0 2 4 5 6 6 7 8 6#: 0 1 2 4 5 6 6 7 8 7#: 0 1 2 4 5 6 6 7 8 Process returned 0 (0x0) execution time : 1.070 s Press any key to continue.
可以看到,经过改进之后,在使用相同的源代码逻辑和同一组数据的情况下,排序次数减少了 1 次。
更改记录:
- 2019 年 05 月 29 日 17 时 17 分,在“冒泡排序算法的排序过程”中新增了一张演示冒泡排序的动图(图 1)并添加了有关说明。
EOF