前言
数列的收敛与发散问题和函数的极限问题有相似之处,但是,由于数列的离散性,因此,数列的收敛与发散又有着一些特殊的性质。【荒原之梦】通过检索发现,互联网上关于此类问题存在一些错误的分析与结论,存在相当程度的误导性。为了使互联网上多一些理性的分析,本文将简要探讨一下收敛数列与发散数列的若干性质并对这些性质给出一定的解释。
正文
收敛数列的定义
如果,当 $n \rightarrow + \infty$ 时,数列 ${a_{n}}$ 趋向于且仅趋向于极限 $A$, 其中,$A$ 是一个常数,则数列 ${a_{n}}$ 就是一个收敛数列。
发散数列的定义
不收敛的数列就是发散的数列,因此,不满足上述收敛数列定义的数列就是发散数列。
数列的有界性和敛散性
总的来说,数列的有界性和敛散性具有如下定理:
- 收敛必有界
- 有界不一定收敛
- 无界必发散
- 发散不一定无界
数列的收敛与发散、有界与无界之间的关系及解释如图 1 所示:
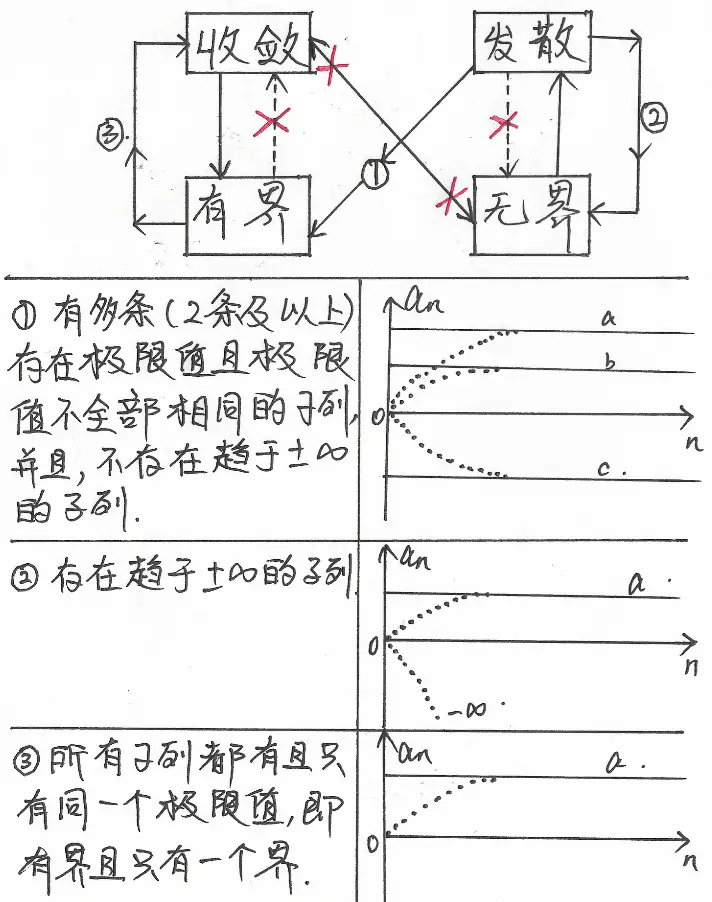
从图 1 可以看出,由于从有界推出收敛还需要在有界的基础上加一些限制条件,因此,根据【前充分后必要,小充分大必要】的原则,可知:
有界是收敛的必要非充分条件。
同理可得:
发散是无界的必要非充分条件;
发散是有界的必要非充分条件。
EOF