七、解答题 (本题满分 9 分)
如图 04, $A, D$ 分别是曲线 $y=\mathrm{e}^{x}$ 和 $y=\mathrm{e}^{-2 x}$ 上的点, $A B$ 和 $D C$ 均垂直 $x$ 轴, 且 $|A B|:|D C|=2: 1,|A B|<1$. 求点 $B$ 和 $C$ 的横坐标, 使梯形 $A B C D$ 的面积最大.
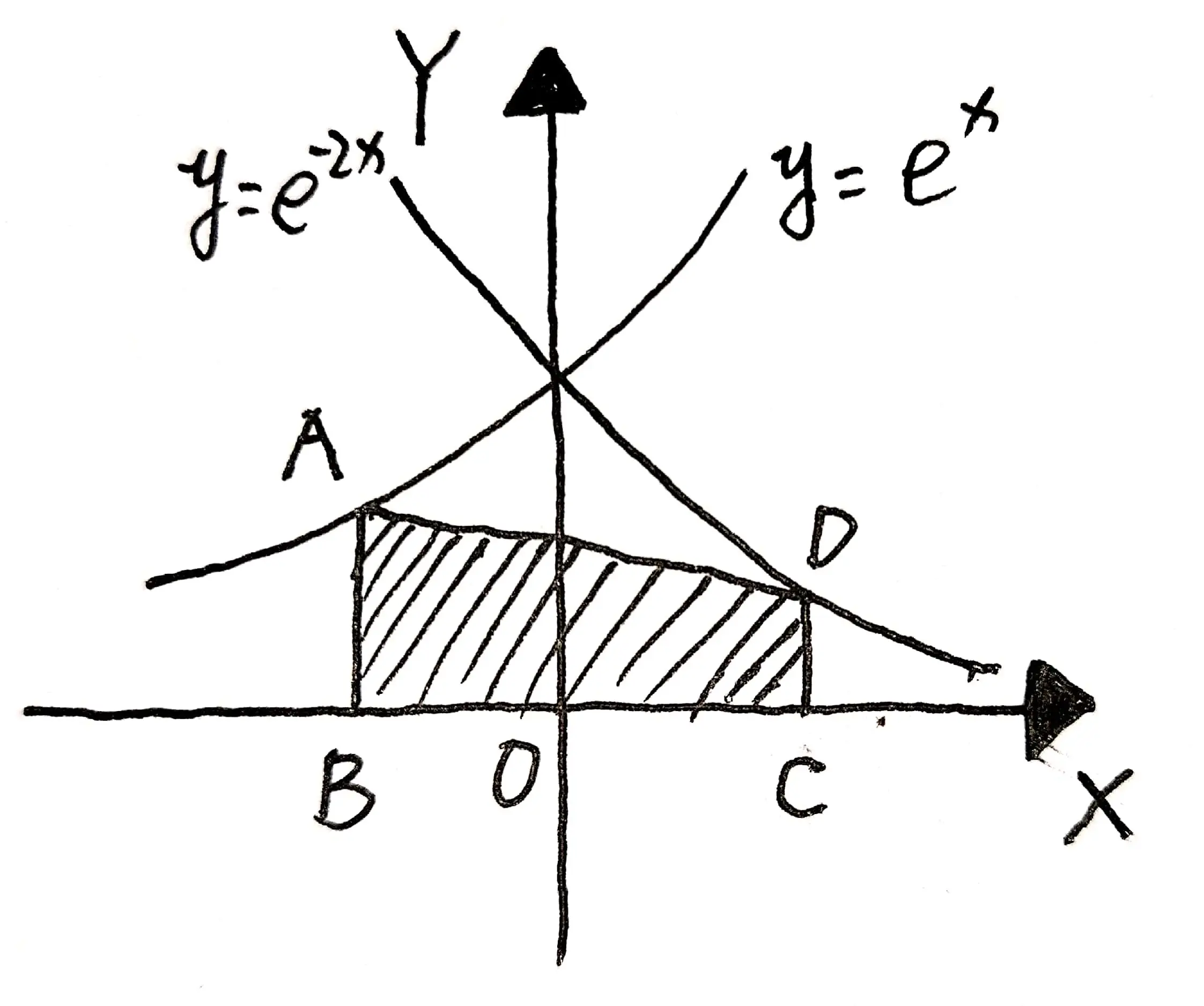
$$
\textcolor{springgreen}{
|A B|=e^{x_{1}}, \quad|C D|=e^{-2 x_{2}}
}
$$
注意:
$$
\textcolor{orangered}{
|A B| \neq e^{-2 x_{1}}|C D| \neq e^{x_{2}}
}
$$
进而:
$$
|A B|=2|C D| \Rightarrow e^{x_{1}}=2 e^{-2 x_{2}} \Rightarrow
$$
$$
x_{1}=\log _{e} 2 e^{-2 x_{2}} = \ln \left(2 e^{-2 x_{2}}\right) \Rightarrow
$$
$$
x_{1}=\ln 2-2 x_{2} \Rightarrow
$$
$$
S=\frac{1}{2}(|A B|+|C D|)\left(x_{2}-x_{1}\right) \Rightarrow
$$
$$
S=\frac{1}{2}\left(3 e^{-2 x_{2}}\right)\left(x_{2}-\ln 2+2 x_{2}\right) \Rightarrow
$$
$$
f\left(x_{1}=\frac{1}{2}\left(3 e^{-2 x_{1}}\right)\left(3 x_{1}-\ln 2\right) \Rightarrow\right.
$$
$$
f^{\prime}(x)=\frac{3}{2} \cdot(-2) e^{-2 x}(3 x-\ln 2)+
$$
$$
\frac{3}{2} \cdot e^{-2 x} \cdot 3 \Rightarrow
$$
$$
f^{\prime}(x)=0 \Rightarrow-2(3 x-\ln 2)+3=0 \Rightarrow
$$
$$
-6 x+2 \ln 2+3=0 \Rightarrow
$$
$$
x=\frac{1}{6}(2 \ln 2+3) \Rightarrow x=\frac{1}{3} \ln 2+\frac{1}{2}
$$
由于计算 $f^{\prime \prime}(x)$ 后再判断是否是极大值太复杂,因此可以采用下面的方法判断是否是极大值:
$$
x<\frac{1}{3} \ln 2+\frac{1}{2} \Rightarrow f^{\prime}(x)>0
$$
$$
x>\frac{1}{3} \ln 2+\frac{1}{2} \Rightarrow f^{\prime}(x)<0
$$
综上可知,当 $x_{2}=\frac{1}{3} \ln 2+\frac{1}{2}$, $x_{1}=\frac{1}{3} \ln 2-1$ 时取得最大的面积。