二、选择题(本题满分 15 分,每小题 3 分)
(1) 若曲线 $y=x^{2}+a x+b$ 和 $2 y=-1+x y^{3}$ 在点 $(1,-1)$ 处相切, 其中 $a, b$ 是常数, 则
(A) $a=0, b=-2$.
(B) $a=1, b=-3$.
(C) $a=-3, b=1$.
(D) $a=-1, b=-1$.
正确选项:D
$$
y=x^{2}+a x+b \Rightarrow y^{\prime}=2 x+a
$$
$$
2 y=-1+x y^{3} \Rightarrow 2 y^{\prime}=y^{3}+3 x y^{2} \cdot y^{\prime} \Rightarrow
$$
$$
y^{\prime}\left(2-3 x y^{2}\right)=y^{3} \Rightarrow y^{\prime}=\frac{y^{3}}{2-3 x y^{2}} \Rightarrow
$$
$$
2 x+a=\frac{y^{3}}{2-3 x y^{2}} \Rightarrow x=1, y=-1 \Rightarrow
$$
$$
2+a=\frac{-1}{2-3}=1 \Rightarrow a=-1
$$
$$
x=1, y=-1 \Rightarrow y=x^{2}+a x+b \Rightarrow
$$
$$
-1=1+a+b \Rightarrow-1=b
$$
(2) 设函数 $f(x)=\left\{\begin{array}{l}x^{2}, \quad 0 \leqslant x \leqslant 1, \\ 2-x, 1<x \leqslant 2,\end{array}\right.$ 记 $F(x)=\int_{0}^{x} f(t) \mathrm{d} t, 0 \leqslant x \leqslant 2$, 则
(A) $F(x)=\left\{\begin{array}{ll}\frac{x^{3}}{3}, & 0 \leqslant x \leqslant 1, \\ \frac{1}{3}+2 x-\frac{x^{2}}{2}, & 1<x \leqslant 2 .\end{array}\right.$
(B) $F(x)=\left\{\begin{array}{ll}\frac{x^{3}}{3}, & 0 \leqslant x \leqslant 1, \\ -\frac{7}{6}+2 x-\frac{x^{2}}{2}, & 1<x \leqslant 2 .\end{array}\right.$
(C) $F(x)=\left\{\begin{array}{ll}\frac{x^{3}}{3}, & 0 \leqslant x \leqslant 1, \\ \frac{x^{3}}{3}+2 x-\frac{x^{2}}{2}, & 1<x \leqslant 2 .\end{array}\right.$
(D) $F(x)=\left\{\begin{array}{ll}\frac{x^{3}}{3}, & 0 \leqslant x \leqslant 1, \\ 2 x-\frac{x^{2}}{2}, & 1<x \leqslant 2 .\end{array}\right.$
正确选项:B
$$
0 \leq x \leq 1 \Rightarrow
$$
$$
F(x)=\int_{0}^{x} f(t) \mathrm{~ d} t=\int_{0}^{x} t^{2} \mathrm{~ d} t=\frac{1}{3} x^{3}
$$
$$
1<x \leqslant 2 \Rightarrow F(x)=\int_{0}^{x} f(t) \mathrm{~ d} t=
$$
$$
\int_{0}^{1} f(t) \mathrm{~ d} t+\int_{1}^{x} f(t) \mathrm{~ d} t=
$$
$$
\int_{0}^{1} t^{2} \mathrm{~ d} t+\int_{1}^{x}(2-t) \mathrm{~ d} t=
$$
$$
\frac{1}{3}+2 x-\frac{1}{2} x^{2}-2+\frac{1}{2}=
$$
$$
-\frac{1}{2} x^{2}+2 x-\frac{7}{6}
$$
(3) 设函数 $f(x)$ 在 $(-\infty,+\infty)$ 内有定义, $x_{0} \neq 0$ 是函数 $f(x)$ 的极大值点, 则
(A) $x_{0}$ 必是 $f(x)$ 的驻点.
(B) $-x_{0}$ 必是 $-f(-x)$ 的极小值点.
(C) $-x_{0}$ 必是 $-f(x)$ 的极小值点.
(D) 对一切 $x$ 都有 $f(x) \leqslant f\left(x_{0}\right)$.
正确选项:B
- 极值点不一定是可导的,A 选项错;
- $-f(x)$ 的极小值点应该是 $x_{0}$, $-x_{0}$ 不一定是极值点,C 选项错;
- 极大值并不一定是最大值,D 选项错。
(4) 设 $D$ 是 $x O y$ 平面上以 $(1,1), \ (-1,1)$ 和 $(-1,-1)$ 为顶点的三角区域, $D_{1}$ 是 $D$ 在第一象 限的部分, 则 $\iint_{D}(x y+\cos x \sin y) \mathrm{d} x \mathrm{~d} y$ 等于
(A) $2 \iint_{D_{1}} \cos x \sin y \mathrm{~d} x \mathrm{~d} y$.
(B) $2 \iint_{D_{1}} x y \mathrm{~d} x \mathrm{~d} y$.
(C) $4 \iint_{D_{1}}(x y+\cos x \sin y) \mathrm{d} x \mathrm{~d} y$.
(D) $0$.
正确选项:A
参考文章:《根据一重积分奇偶对称的性质记忆二重积分奇偶对称的性质》
根据题目我们可以绘制出如下示意图,并将积分区域 $D$ 划分为 $D_{1}$, $D_{2}$, $D_{3}$ 和 $D_{4}$ 四个部分:
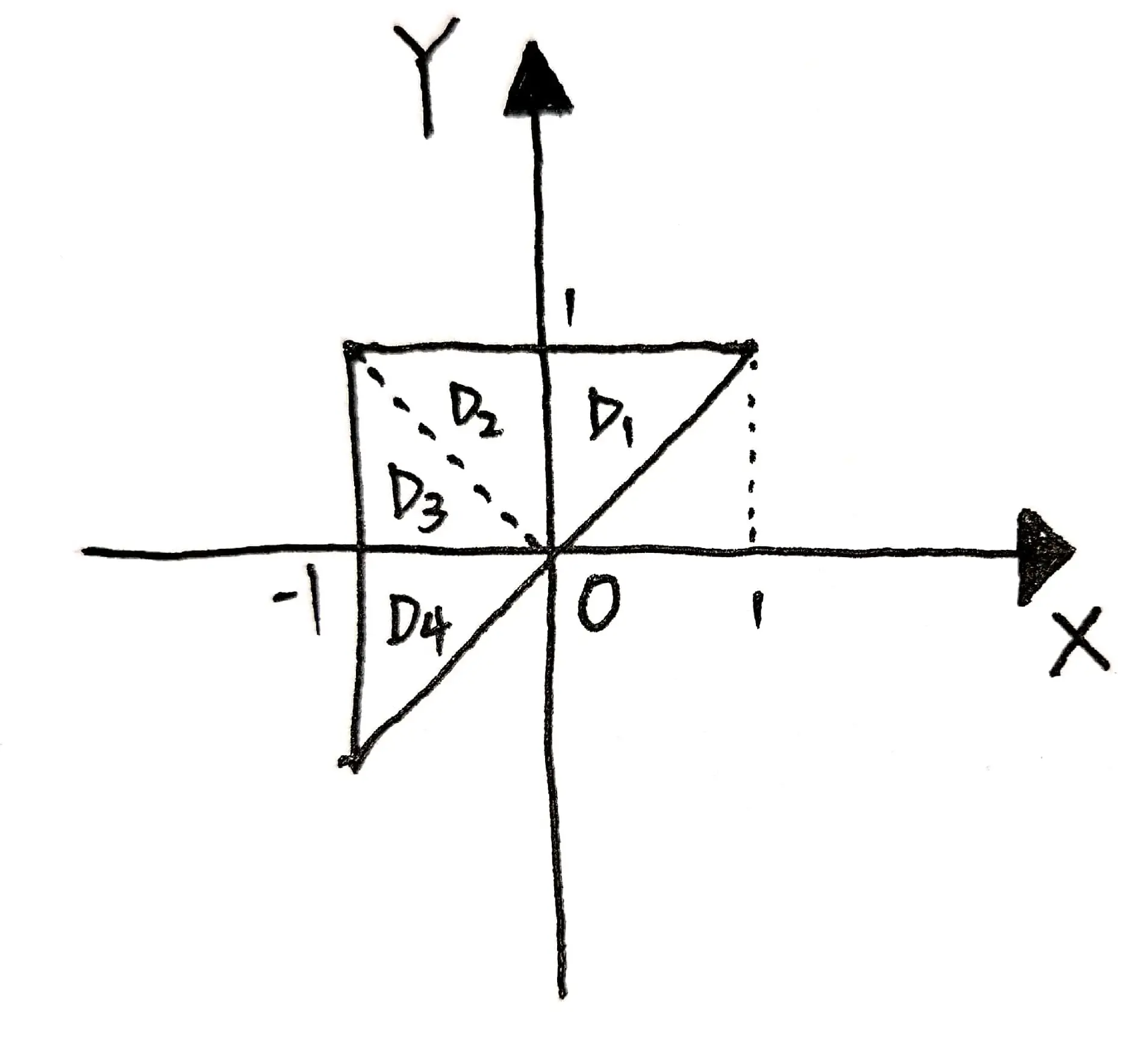
于是:
$$
\iint_{D}(x y-\cos x \sin y) \mathrm{~ d} x \mathrm{~ d} y \Rightarrow
$$
$$
I_{1}=\iint_{D} x y \mathrm{~ d} x \mathrm{~ d} y \quad I_{2}=\iint_{D} \cos x \sin y \mathrm{~ d} x \mathrm{~ d} y
$$
$$
\iint_{D_{1}+D_{2}} x y=0 \quad \iint_{D_{3}+D_{4}} x y=0
$$
$$
\iint_{D_{1}+D_{2}} \cos x \sin y=2 \iint_{D_{1}} \cos x \sin y
$$
$$
\iint_{D_{3}+D_{4}} \cos x \sin y=0
$$
(5) 如图 02, $x$ 轴上的一线密度为常数 $\mu$, 长度为 $l$ 的细杆, 有一质量为 $m$ 的质点到杆右端的距离为 $a$, 已知引力系数为 $k$, 则质点和细杆之间引力的大小为
(A) $\int_{-l}^{0} \frac{k m \mu \mathrm{d} x}{(a-x)^{2}}$.
(B) $\int_{0}^{l} \frac{k m \mu \mathrm{d} x}{(a-x)^{2}}$.
(C) $2 \int_{-\frac{l}{2}}^{0} \frac{k m \mu \mathrm{d} x}{(a+x)^{2}}$.
(D) $2 \int_{0}^{\frac{l}{2}} \frac{k m \mu \mathrm{d} x}{(a+x)^{2}}$.
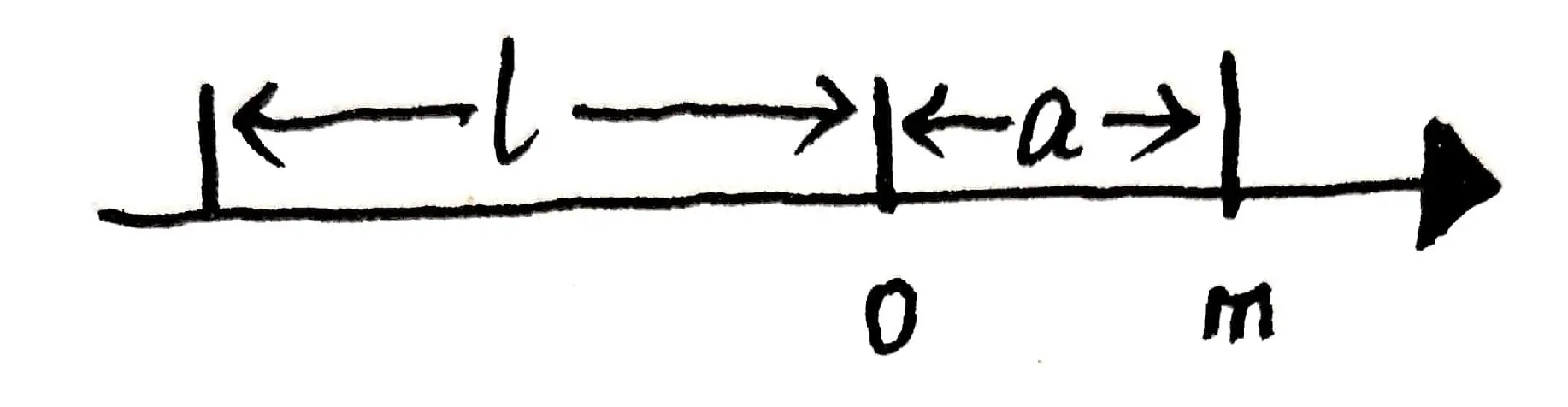
正确选项:A
参考文章:《高等数学物理应用:质点间引力的计算公式》
首先,绘制出如下坐标系:

$$
F=G \frac{M m}{r^{2}} \Rightarrow \mathrm{d} F=k \frac{m \cdot \mu \mathrm{~ d} x}{[\alpha+(-x)]^{2}} \Rightarrow
$$
$$
\mathrm{d} F=\frac{k m \mu \mathrm{~ d} x}{(a-x)^{2}} \Rightarrow F=\int_{-l}^{0} \frac{k m \mu}{(a-x)^{2}} \mathrm{~ d} x
$$