题目
标题:切面条
一根高筋拉面,中间切一刀,可以得到2根面条。
如果先对折1次,中间切一刀,可以得到3根面条。
如果连续对折2次,中间切一刀,可以得到5根面条。
那么,连续对折10次,中间切一刀,会得到多少面条呢?
答案是个整数,请通过浏览器提交答案。不要填写任何多余的内容。
题目分析
本题其实可以不需要使用编程的方式解决, 这是一个数列找规律的问题. 对于找规律的问题需要记住的一点就是要手算出尽可能多的项, 这样找出来的规律才比较可靠 (题目中已经给出了数列的前三个值, 如果最终的规律可以靠前三个数列导出的话, 那么这道题就没什么考点了, 因此至少需要计算出数列中第 4 个数的值).
数列的规律可以从以下几个方面寻找:
- 两个数值间的关系是否和两个数之间的差值有关系, 差值的变化是否具有某种规律, 例如呈指数增长的差值;
- 前两个数的和 (或者差, 积, 商) 是否可以得出其后的数.
通过使用 Windows 系统中的”画图”工具绘制出前 4 种情况(如果时间充裕的话可以在得出结果后绘制第 5 种情况以验证对规律的猜测是否正确), 如图 1
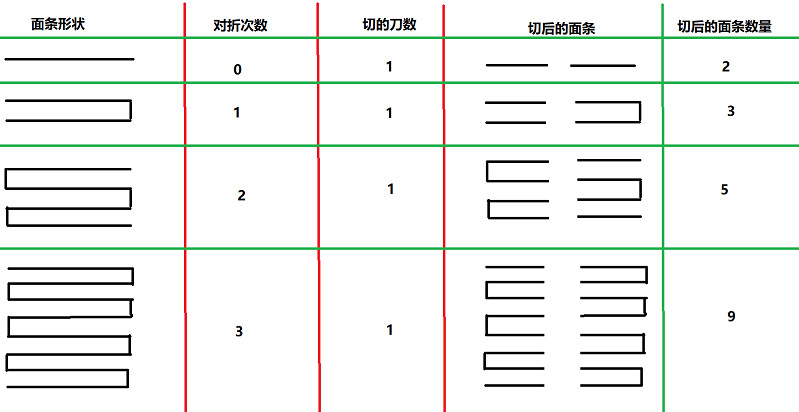
由此, 我们可以得到关于面条个数的这样一个数列:
2, 3, 5, 9
接着我们可以得到这样一个规律:
2+0=2 (对折 0 次) 2+1=3 (对折 1 次) 3+2=5 (对折 2 次) 5+4=9 (对折 3 次)
进而得到:
2+2^0=3 (对折 1 次) 3+2^1=5 (对折 2 次) 5+2^2=9 (对折 3 次)
规律找到这里, 我们可以使用程序进行之后的计算, 程序如下:
#include<iostream>
#include<bits/stdc++.h>
using namespace std;
int main(){
int a=2;
int ans=2;
for(int i=0;i<=9;i++){
ans=ans+pow(a,i);
}
cout<<ans<<endl;
return 0;
}
程序运行结果:
1025
如果不知道 C/C++ 用于求次方的函数是什么, 也可以使用循环代替, 下面的程序同样可以计算出最终结果:
#include<iostream>
#include<bits/stdc++.h>
using namespace std;
int main(){
int ans=5;
for(int i=2;i<=9;i++){
int b=2;
int a=2;
for(int j=1;j<i;j++){
b=b*a; //a 在循环的过程中必须始终为 2
}
ans=ans+b;
}
cout<<ans<<endl;
return 0;
}
程序运行结果:
1025
在运行程序之前可以先设置断点进行单步调试, 看看程序运行的前几步是不是和我们手动计算出来的结果 (和规律) 一致.
另外, 正如本文开头所说的, 本题可以不通过编程的方式解决, 因为这可以看做是一个数学问题, 就是找数列的规律. 但是为什么我们上面找到数列的规律后还需要用程序计算呢? 因为上面得到的规律中, 等号左边的变量有两个, 每一步的计算都需要上一步的结果作为支撑 (当然, 也可以不编程, 直接借助系统中的计算器逐步计算, 这个方法也可以用于对程序计算结果的验证), 每一步的计算都不是独立的, 这样的规律显然不适合手算, 之前找到的规律如下:
2+2^0=3 (对折 1 次) 3+2^1=5 (对折 2 次) 5+2^2=9 (对折 3 次)
为了方便手算, 我们必须想办法去掉一个变量, 于是, 就有了下面这个规律:
1+2^0+2^0=3 (对折 1 次) 1+2^1+2^1=5 (对折 2 次) 1+2^2+2^2=9 (对折 3 次)
进而得到:
1+2*2^0=3 (对折 1 次) 1+2*2^1=5 (对折 2 次) 1+2*2^2=9 (对折 3 次)
进而又可得到:
1+2^1=3 (对折 1 次) 1+2^2=5 (对折 2 次) 1+2^3=9 (对折 3 次)
在上面的规律中, 对每次对折的求解都不依赖上一次对折得出的相关数值, 变量只有一个, 即对折的次数, 因此可以通过一次计算就得出对折 10 次后再在中间切一刀能够得到的面条个数, 计算过程与结果为:
1+2^10=1025
本题需要注意的一点是, 得到两根面条的时候 (第 1 次切的时候) 对折的次数是 0 次.
本题的关键是正确地找出数列中的多个数值, 如果只找出前三个数值则本题很可能会得出错误的结果.