前言
本文将给出在对【上三角矩阵】、【下三角矩阵】和【三对角矩阵】以【行主序】方式在【一维数组】中压缩存储时元素存储地址的计算方法以及图像示例，以作参考。
继续阅读“对上/下三角矩阵和三对角矩阵压缩存储时元素存储地址的计算方法”分类： 数据结构
数据结构之于计算机程序，如同 DNA 之于生物体。
[数据结构基础]二叉树的重要性质
[数据结构基础]使用顺序存储方式存储多维数组时特定元素存储地址的计算方法
前言
本文将分析并给出将一维数组、二维数组和三维数组使用顺序存储方式存储时确定给定的某个数组元素在内存中的存储地址的计算方法，以作参考。
继续阅读“[数据结构基础]使用顺序存储方式存储多维数组时特定元素存储地址的计算方法”递归 (一): 递归思想与 C++ 中的递归函数及两个递归应用示例 (斐波那契, 汉诺塔)
什么是递归
从汇编层面上看递归
在汇编层面上, 递归可以看作是两个循环, 每个循环的循环参数都由另一个循环传入
从算法思想上看递归
递归是基于分治的, 也就是”分而治之”. 当需要求解的问题的输入规模为 N, 而 N 又很大的时候, 直接按照线性过程求解将十分困难. 这个时候, 如果 N 具有某些特性, 能够被分解成更小规模的问题 n, 并且这些小规模的问题 n 满足以下条件:
- 由全部 n 的解能够得出 N 的解;
- 全部 n 之间互相独立, n 与 n 之间不存在公共区域.
这时, 我们就可以考虑使用”分支”来对 N 进行求解. 如果求解小规模问题 n 的方法和求解大规模问题 N 的方法是一致的 (n 具有 N 的最优子结构性质), 那么这时候就可以考虑更进一步地使用递归的思想求解.
从高级程序语言形式上看递归
在高级语言中, 递归的表现形式就是一个函数直接或间接地调用了自己, 直到满足出口条件, 结束递归.
从语义上看递归
“递归”分开就是”递”和”归”, “递”是离开自己, “归”是回到自己. 中文中的”递归”一词也表明了递归函数是一个来回往复的运算过程. 在英文中, “递归”的英文是”recursion”, “recursion”包含”重复”的意思. 另外, “递归”与”循环”在语义上也有明显的区别, “递归 (recursion)”是一个一维的往复结构, 而”循环 (loop)”则是一个二维的环状结构.
C++ 中的递归函数示例
斐波那契数列 (Fibonacci sequence)
斐波那契数列来源于斐波那契在其著作《计算之术》中提出的一个问题:
在第一个月有一对刚出生的小兔子，在第二个月小兔子变成大兔子并开始怀孕，第三个月大兔子会生下一对小兔子，并且以后每个月都会生下一对小兔子。 如果每对兔子都经历这样的出生、成熟、生育的过程，并且兔子永远不死，那么兔子的总数是如何变化的？
斐波那契《计算之术》
对于上面这个问题我们可以得出这样一个过程:
第 01 个月: 01 只小兔子 –> 01
第 02 个月: 01 只大兔子 –> 01
第 03 个月: 01 只大兔子 + 01 只小兔子 –> 02
第 04 个月: 02 只大兔子 + 01 只小兔子 –> 03
第 05 个月: 03 只大兔子 + 02 只小兔子 –> 05
第 06 个月: 05 只大兔子 + 03 只小兔子 –> 08
第 07 个月: 08 只大兔子 + 05 只小兔子 –> 13
…
于是, 我们得到了这样一个数列:
1,1,2,3,5,8,13,21,34…
这就是斐波那契数列 (也叫”兔子数列”).
我们先来借助 for 循环, 使用迭代来计算前 30 位斐波那契数列, 程序如下:
#include<stdio.h>
#include<bits/stdc++.h>
using namespace std;
#define MAX_SIZE 30
int main(){
int a[MAX_SIZE];
a[0]=0;
a[1]=1;
printf("%d ",a[1]);
for(int i=2;i<=MAX_SIZE;i++){
a[i]=a[i-1]+a[i-2];
printf("%d ",a[i]);
}
return 0;
}
运行结果:
1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181 6765 10946 17711 28657 46368 75025 121393 196418 317811 514229
迭代实现的求解斐波那契数列很好理解, 下面使用递归来实现一下.
下面的程序可以计算斐波那契数列中指定位置的值, 程序如下:
#include<stdio.h>
#include<bits/stdc++.h>
using namespace std;
int f(int n){
if(n==0){
return 1;
//斐波那契数列的首位是 1, 因此返回 1
}else if(n==1){
return 1;
//斐波那契数列的第 2 位是 1, 因此返回 1
}else{
return f(n-1)+f(n-2);
//从斐波那契数列的第 3 位及以后开始都可以使用前面两位的和计算出
}
}
int main(){
int a=f(7); //返回斐波那契数列的第 7 个值(从 0 开始计算)
printf("%d\n",a);
system("pause");
return 0;
}
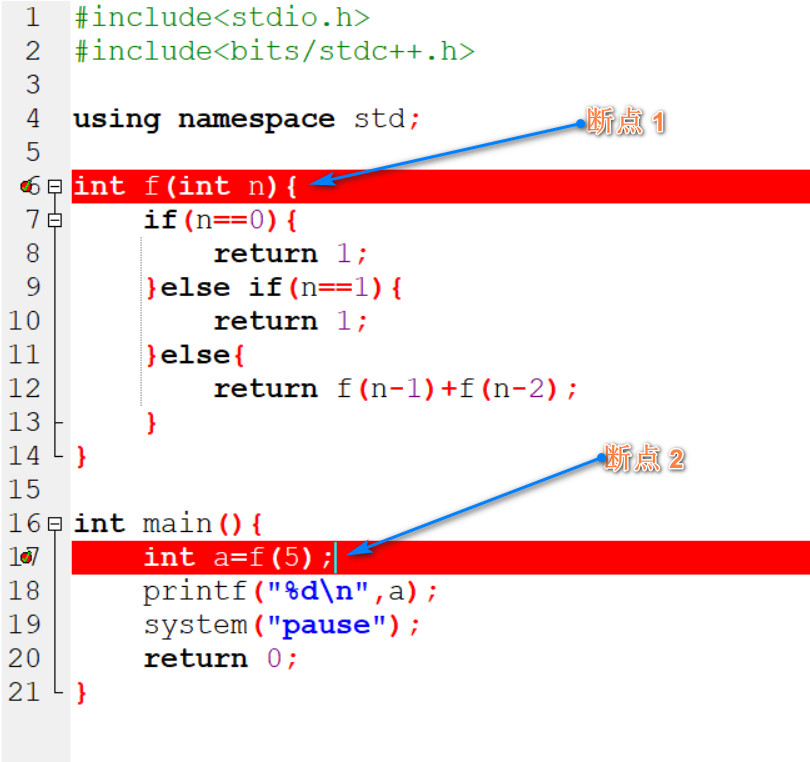
为了搞清楚递归的函数调用过程, 我们对上面的程序设置两个断点, 之后采用”单步进入”的方式逐步观察计算过程, 为了方便说明, 我们将函数 f() 的参数设置为 5, 即:
int a=f(5);
断点设置情况如下:
下面开始逐步分析展示本次调试过程:
01: a 为一个随机的初始值 31.
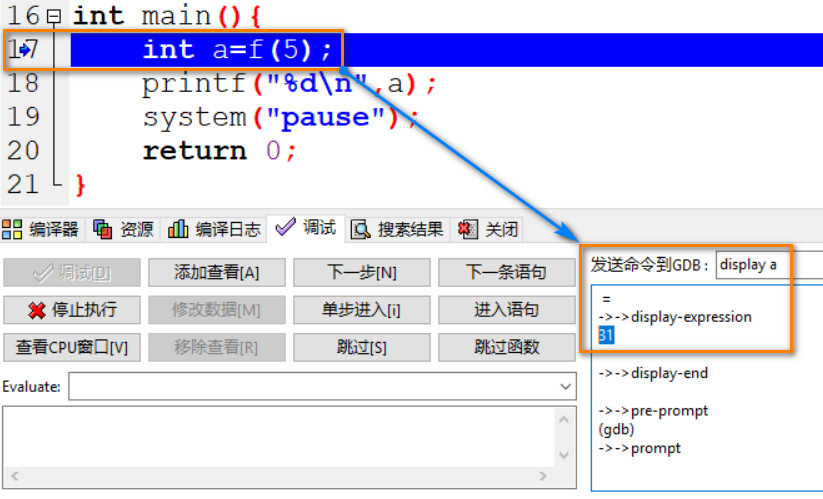
02: 参数 5 被传递给函数 f(n), n=5.
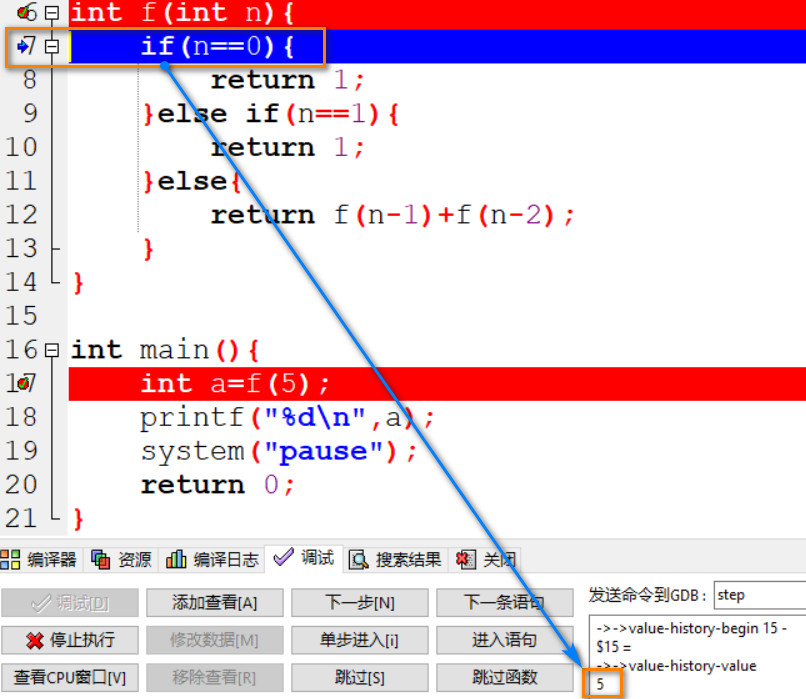
03: n 进入 else if 语句并和 1 对比判断是否相等, 此时 n=5.
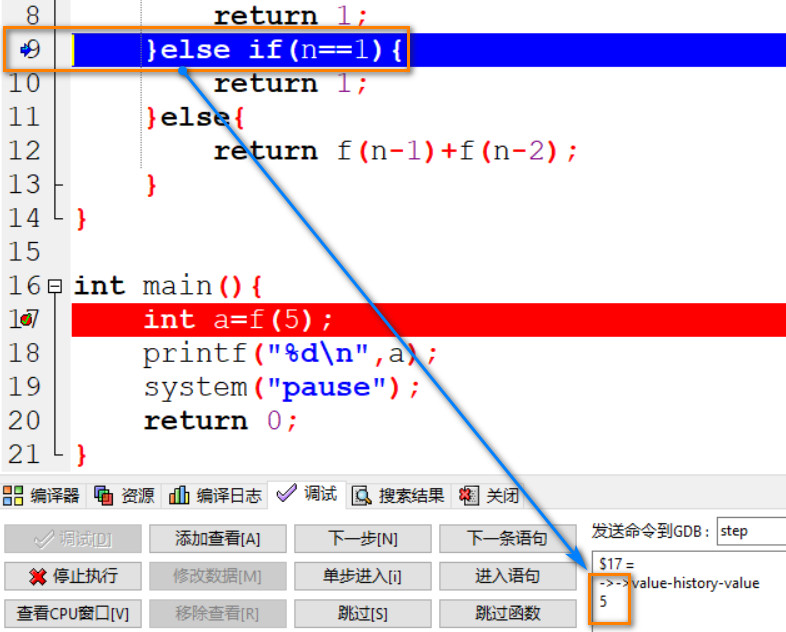
04: 由于 5!=1, n 进入 else 语句, 此时 return f(5-1)+f(5-2);
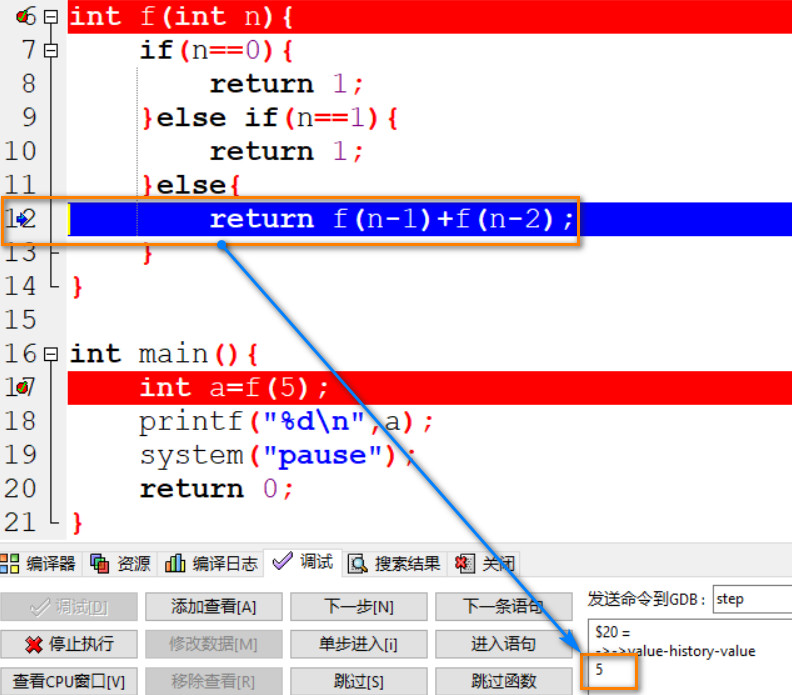
05: 由于不知道上一步需要的 f(4) 和 f(3) 的值, 因此 n-1=4 并重新执行 f(n) 函数, 此时 n=4.
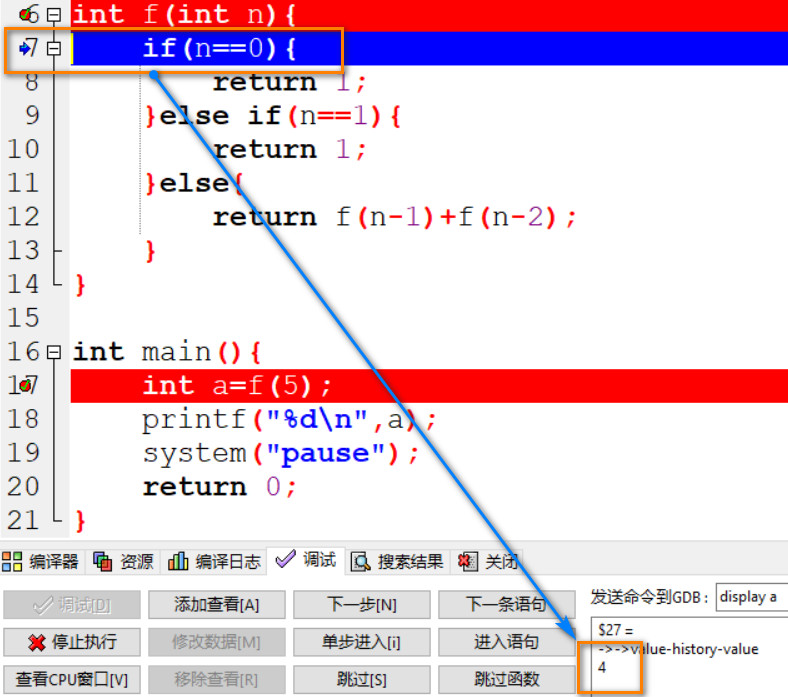
06: n 进入 else if 语句并和 1 对比判断是否相等, 此时 n=4.
07: 由于 4!=1, n 进入 else 语句, 此时 return f(4-1)+f(4-2);
08: 由于不知道上一步需要的 f(3) 和 f(2) 的值, 因此 n-1=3 并重新执行 f(n) 函数, 此时 n=3.
09: n 进入 else if 语句并和 1 对比判断是否相等, 此时 n=3.
10: 由于 3!=1, n 进入 else 语句, 此时 return f(3-1)+f(3-2);
11: 由于不知道上一步需要的 f(2) 和 f(1) 的值, 因此 n-1=2 并重新执行 f(n) 函数, 此时 n=2.
12: n 进入 else if 语句并和 1 对比判断是否相等, 此时 n=2.
13: 由于 2!=1, n 进入 else 语句, 此时 return f(2-1)+f(2-2);
14: 由于不知道上一步需要的 f(1) 和 f(0) 的值, 因此 n-1=1 并重新执行 f(n) 函数, 此时 n=1.
15: n 进入 else if 语句并和 1 对比判断是否相等, 此时 n=1, 由于 1=1 为真, 因此返回 1 并跳出 if 判断语句:
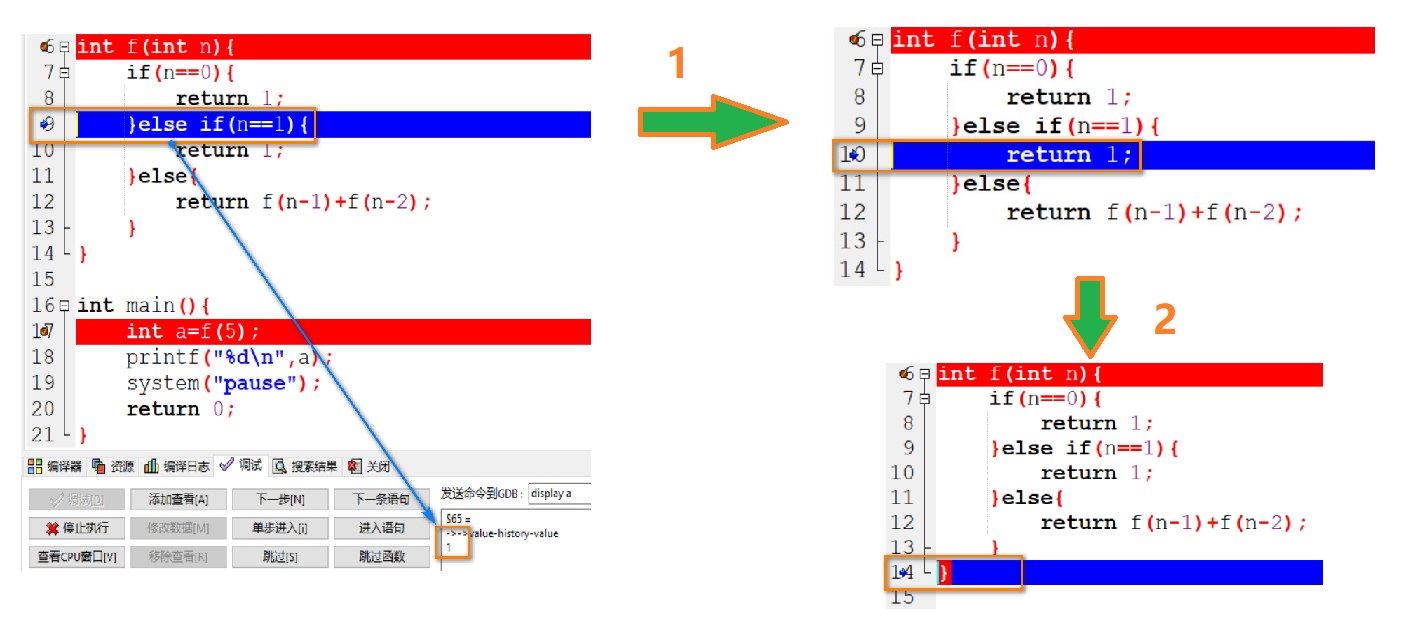
16: 经过上面的步骤知道了 f(1) 的值, 但是还不知道 f(0) 的值, 因此 n-1=1 并重新执行 f(n) 函数, 此时 n=0. 由于 0=0 为真, 因此返回 1, 至此, 边界条件 f(0) 和 f(1) 的值都知道了.
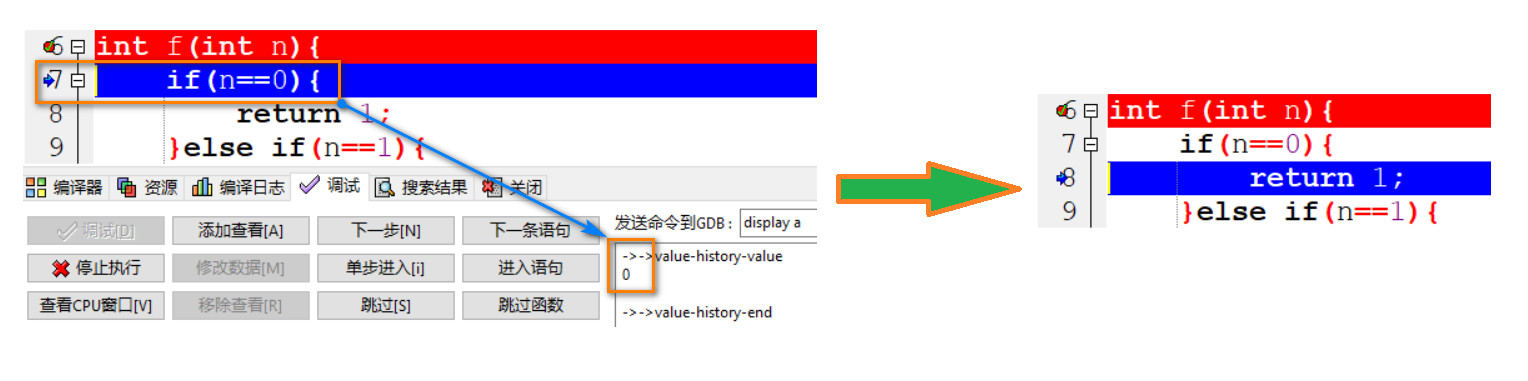
(后续过程不再使用文字描述, 见下面的图片说明.)
这个过程其实就是一个二叉树的遍历过程, 我用图片的形式绘制了整个过程, 如图 9:
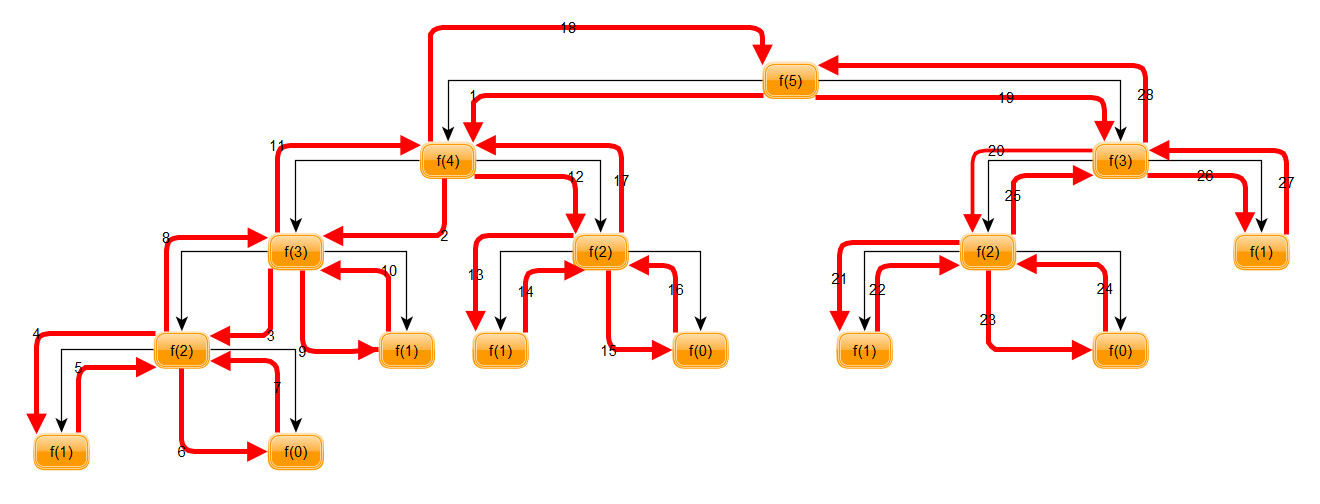
上面这个程序运行一次只能输出斐波那契数列中的一个数值, 下面对该程序进行一个改进, 使得可以输出指定的前 n 位的斐波那契数列, 程序如下:
#include<stdio.h>
#include<bits/stdc++.h>
using namespace std;
int f(int n){
if(n==0){
return 1;
}else if(n==1){
return 1;
}else{
return f(n-1)+f(n-2);
}
}
int main(){
int n=5; //设置打印前 6 个斐波那契数列元素
for(int i=0;i<=n;i++){
int a=f(i);
printf("%d ",a);
}
system("pause");
return 0;
}
上述程序的运行结果是:
1 1 2 3 5 8
汉诺塔 (Tower of Hanoi)
Wikipedia 上对于汉诺塔问题的说明如下:
The Tower of Hanoi (also called the Tower of Brahma or Lucas’ Tower and sometimes pluralized) is a mathematical game or puzzle. It consists of three rods and a number of disks of different sizes, which can slide onto any rod. The puzzle starts with the disks in a neat stack in ascending order of size on one rod, the smallest at the top, thus making a conical shape.
The objective of the puzzle is to move the entire stack to another rod, obeying the following simple rules:
1. Only one disk can be moved at a time.
2. Each move consists of taking the upper disk from one of the stacks and placing it on top of another stack or on an empty rod.
3. No larger disk may be placed on top of a smaller disk.With 3 disks, the puzzle can be solved in 7 moves. The minimal number of moves required to solve a Tower of Hanoi puzzle is 2n − 1, where n is the number of disks.
Wikipedia, Source: https://en.wikipedia.org/wiki/Tower_of_Hanoi
原始的汉诺塔问题是一个来自于印度的数学游戏, 在该游戏中, 有三根柱子, 其中一根柱子上有 64 个圆盘, 且这些圆盘都按照较大的圆盘在较小的圆盘下面的原则放置, 如图 10:
现在要把这些圆盘从目前的柱子上移动到另外两根柱子的其中一根上, 要求如下:
- 一次只能移动一个圆盘.
- 大圆盘必须始终在小圆盘的下面.
汉诺塔问题十分适合使用递归来解决, 使用”分治”的思想来思考这个问题就能找到解决问题的思路. 我们首先考虑如果这个汉诺塔问题只有两个圆盘时该如何移动圆盘(假设三个柱子从左向右依次为 A, B, C):
- 把 A 上较小的圆盘放到 B 上
- 把 A 上较大的圆盘放到 C 上
- 把 B 上较小的圆盘放到 C 上
通过这三步, 将 B 柱作为一个中转柱, 我们就完成了把 A 上的圆盘全部转移到 C 上任务, 整个过程都符合汉诺塔的游戏规则.
但是, 我们现在有 64 个圆盘, 不是 2 个圆盘, 这该怎么办呢? 我们这时可以用”分治”的思想来想想看. 如图 11, 我们把 A 柱上较小的 63 个圆盘看作一个圆盘, 把下面最大的那个圆盘看作 1 个圆盘, 这样就成了”两个圆盘”, 因此可以使用上面关于只有两个圆盘时的移动方式来解决这个问题, 过程都显示在下面的图片里了:
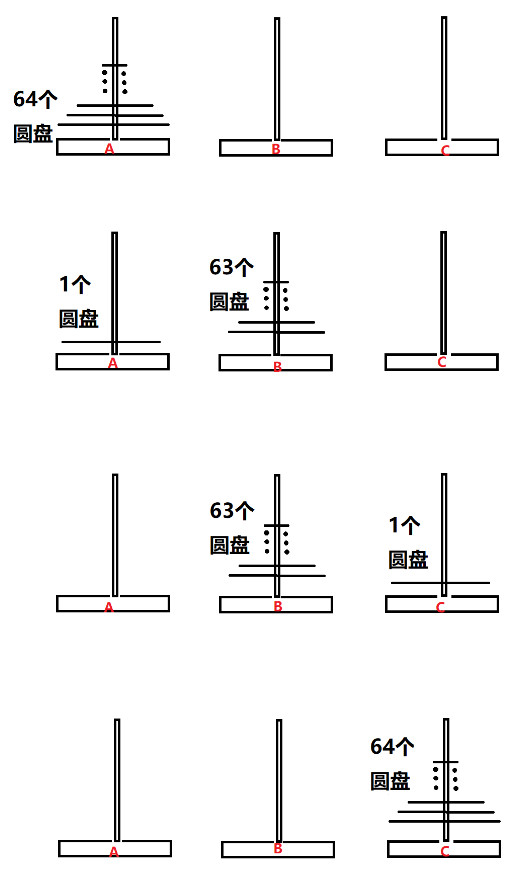
那么之后该怎么做呢?
当我们把最大的一个圆盘移动到 C 上, 把 63 个较小的圆盘移动到 B 上之后, 即图 11 中的第 3 步, 我们可以发现, 此时圆盘的分布和图 11 中的第 2 步是很相似的, 只不过空出来的柱子由 C 变成了 A, 于是, 就有了下面这个过程:
- 把 A 柱上的前 63 个圆盘移动到 B 柱 (此时 B 柱作为中转);
- 把 A 柱上的第 64 个圆盘移动到 C 柱;
- 把 B 柱上的前 62 个圆盘移动到 A 柱 (此时 A 柱作为中转);
- 把 B 柱上的第 63 个圆盘移动到 C 柱;
- 把 A 柱上的前 61 个圆盘移动到 B 柱 (此时 B 柱作为中转);;
- 把 A 柱上的第 62 个圆盘移动到 C 柱;
…
将多个圆盘看作是一个圆盘与真的是一个圆盘其实是一样的. 下面我们从递归的程序角度思考一下这个过程:
- 如果要移动第 64 个, 必须先移动完前 63 个;
- 如果要移动第 63 个, 必须先移动完前 62 个;
- 如果要移动第 62 个, 必须先移动完前 61 个;
- (…省略若干行…)
- 如果要移动第 2 个, 必须先移动完第 1 个;
- 第 1 个是可以自由移动的, 于是, 我们把第 1 个移动到 B 柱(由于不是只有 1 个圆盘, 因此第 1 个圆盘要去中转柱而不是最终的目标柱);
- 现在可以把第 2 个移动到 C 柱了;
- 但是 A 柱上的圆盘并没有被移动完, 为了能移动完, 我们现在必须想办法让第 3 个圆盘到 C 柱(之后以此类推可以让第 4,5,6…64个圆盘到 C 柱);
- 于是, 我们把第 1 个圆盘从 B 柱移动到 A 柱, 把第 2 个圆盘从 C 柱移动到 B 柱, 把 第 1 个圆盘从 A 柱移动到 B 柱, 把第 3 个圆盘从 A 柱移动到 C 柱.
- 好啦, 现在第 3 个圆盘成功的到了 C 柱.
- 不过还没完, 我们需要重复上面的过程, 直到把第 64 个圆盘移动到 C 柱, 之后, 第 64 个圆盘在之后的移动过程中就可以不用动了, 一直待在 C 柱上.
- 对于剩下的 63 个圆盘重复和原来 64 个圆盘一样的移动过程即可.
这么移动的工作量是很大的, 移动完全部 64 个圆盘需要大约 1800 亿亿步:
18,446,744,073,709,551,615
根据上面的介绍, 用 C++ 实现的话, 程序是这样的:
#include<iostream>
#include<bits/stdc++.h>
using namespace std;
//假设函数 (int n, char a, char b, char c) 的作用是将 n 个圆盘从 a 移动到 c
void f(int n, char a, char b, char c){
if(n==1){
cout<<"将盘子"<<n<<"从"<<a<<"移动到"<<c<<endl;
//当只有 1 个盘子时, 直接从 a 移动到 c
}else{
f(n-1,a,c,b);
//将 n-1 个圆盘由 a 移动到 b
cout<<"将盘子"<<n<<"从"<<a<<"移动到"<<c<<endl;
f(n-1,b,a,c);
//将 n-1 个圆盘由 b 移动到 c
}
}
int main(){
f(3,'a','b','c');
return 0;
}
上面这个程序的运行结果如下 (圆盘的序号越大则圆盘越大):
假设有三个圆盘, 移动顺序是这样的:
- 将盘子1从a移动到c
- 将盘子2从a移动到b
- 将盘子1从c移动到b
- 将盘子3从a移动到c
- 将盘子1从b移动到a
- 将盘子2从b移动到c
- 将盘子1从a移动到c
假设有四个圆盘, 移动顺序是这样的:
- 将盘子1从a移动到b
- 将盘子2从a移动到c
- 将盘子1从b移动到c
- 将盘子3从a移动到b
- 将盘子1从c移动到a
- 将盘子2从c移动到b
- 将盘子1从a移动到b
- 将盘子4从a移动到c
- 将盘子1从b移动到c
- 将盘子2从b移动到a
- 将盘子1从c移动到a
- 将盘子3从b移动到c
- 将盘子1从a移动到b
- 将盘子1从a移动到b
- 将盘子2从a移动到c
- 将盘子1从b移动到c
最后, 来看几个关于汉诺塔问题的动图吧.
图 12:
图 12 By André Karwath aka Aka – Own work, CC BY-SA 2.5, https://commons.wikimedia.org/w/index.php?curid=85401
图 13:
2015 年蓝桥杯 C 语言 B 组省赛第 1 题: 奖券数目 (四种解法 + 详细分析)
题目
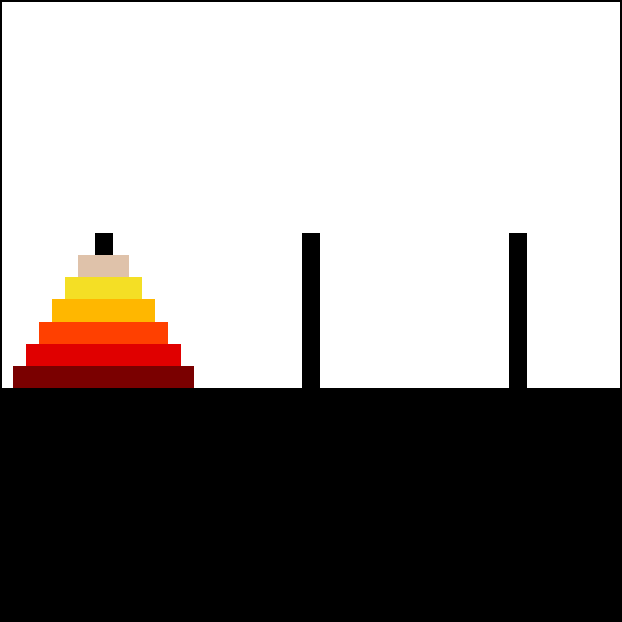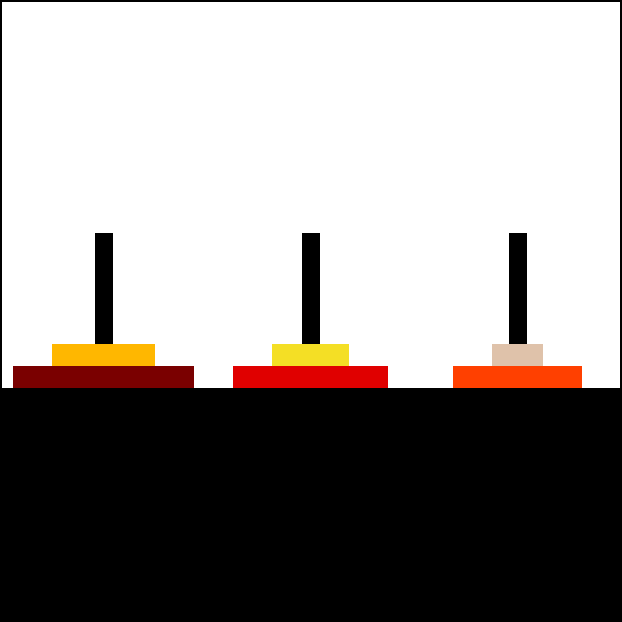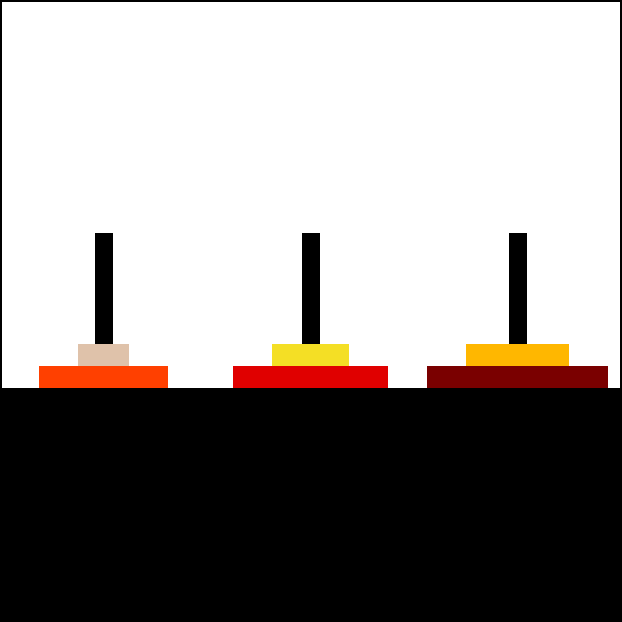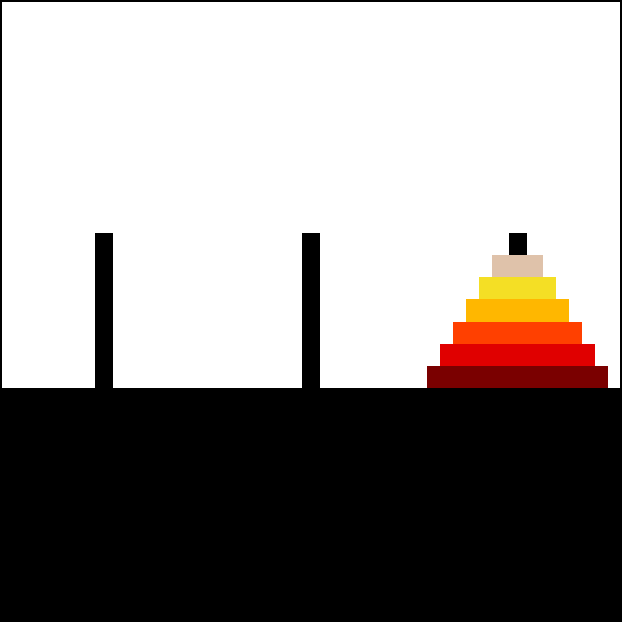
奖券数目
有些人很迷信数字，比如带“4”的数字，认为和“死”谐音，就觉得不吉利。 虽然这些说法纯属无稽之谈，但有时还要迎合大众的需求。某抽奖活动的奖券号码是5位数（10000-99999），要求其中不要出现带“4”的号码，主办单位请你计算一下，如果任何两张奖券不重号，最多可发出奖券多少张。
请提交该数字（一个整数），不要写任何多余的内容或说明性文字。
题目分析
本题的主要解题思路就是枚举 10000-99999 之间的所有数字, 然后判断其中是否含有 4 , 如果不含有 4 则计数器加 1.
在具体实现上, 有四种解法. 第一种解法是对每个枚举结果都进行分解, 将原来的 5 位数分解成 5 个 1 位数, 之后逐个数字判断是否含有数字 4; 第二种方法是把每个枚举的结果都转换成字符串, 之后判断这个字符串中是否包含字符”4″, 如果不包含则计数器加 1; 第三种解法是使用 5 个 for 循环, 模拟奖券的五位数, 之后进行枚举和判断; 第四种解法是使用数学方法求解. 由于除了数字 4 之外, 一共有 9 个数字可以使用, 而且最高位不能为 0, 那么可以计算出符合条件的个数为:
8*9*9*9*9=52488
本题的正确答案是:
52488
下面针对上述分析, 分别求解如下.
方法一
将 10000-99999 之间的所有 5 位数都逐个分解成 5 个 1 位数, 之后逐个数字判断是否为数字 4.
程序:
#include<iostream>
using namespace std;
int main(){
int ans = 0;
for(int i=10000;i<=99999;i++){
//将每一位上的数字都分离出来
//(i%1000) 取余将去掉当前最高位后形成新的数字
//(i%10000)-(i%1000) 将把当前最高位之后的数字都变成 0
//((i%10000)-(i%1000))/1000 将去掉最高位后面的 0, 形成一个个位数
int a = (i-(i%10000))/10000;
int b = ((i%10000)-(i%1000))/1000;
int c = ((i%1000)-(i%100))/100;
int d = ((i%100)-(i%10))/10;
int e = (i%10);
//如果每个位上的数字都不是 4 则计数器加 1
if(a!=4&&b!=4&&c!=4&&d!=4&&e!=4){
ans++;
}
}
cout<<ans<<endl;
return 0;
}
方法二
把 10000-99999 之间的每个枚举的结果都转换成字符串, 之后判断这个字符串中是否包含字符”4″.
程序:
#include<iostream>
#include<bits/stdc++.h>
using namespace std;
void i2s(int num, string &str){
//stringstream 类的作用是将数字转换成字符串
stringstream ss;
//将需要转换的数字 sum 使用 << 运算符传递给 ss 对象
ss << num;
//将转换后的字符串使用 >> 运算符传递给 str 变量
ss >> str;
}
int main(){
int ans=0;
for(int i=10000;i<=99999;i++){
string s;
i2s(i,s);
//查找字符串 s 中是否不包含(注意: 不包含用的是 ==)'4'这个字符串
if(s.find('4')==string::npos){
ans++;
}
}
cout<<ans<<endl;
return 0;
}
方法三
使用 5 个 for 循环, 模拟奖券的五位数, 之后进行枚举和判断. 程序:
#include<iostream>
#include<bits/stdc++.h>
using namespace std;
int main(){
int ans=0;
for(int a=1;a<=9;a++){
if(a!=4){
for(int b=0;b<=9;b++){
if(b!=4){
for(int c=0;c<=9;c++){
if(c!=4){
for(int d=0;d<=9;d++){
if(d!=4){
for(int e=0;e<=9;e++){
if(e!=4){
ans++;
}
}
}
}
}
}
}
}
}
}
cout<<ans<<endl;
return 0;
}
方法四
由于除了数字 4 之外, 一共有 9 个数字可以使用, 而且最高位不能为 0, 那么可以计算出符合条件的奖券个数为:
8*9*9*9*9=52488
2015 年蓝桥杯 C 语言 B 组省赛第 4 题: 格子中输出 (详细分析)
题目
格子中输出
StringInGrid函数会在一个指定大小的格子中打印指定的字符串。 要求字符串在水平、垂直两个方向上都居中。 如果字符串太长，就截断。 如果不能恰好居中，可以稍稍偏左或者偏上一点。
下面的程序实现这个逻辑，请填写划线部分缺少的代码。
#include <stdio.h>
#include <string.h>
void StringInGrid(int width, int height, const char* s)
{
int i,k;
char buf[1000];
strcpy(buf, s);
if(strlen(s)>width-2) buf[width-2]=0;
```
printf("+");
for(i=0;i<width-2;i++) printf("-");
printf("+\n");
for(k=1; k<(height-1)/2;k++){
printf("|");
for(i=0;i<width-2;i++) printf(" ");
printf("|\n");
}
printf("|");
printf("%*s%s%*s",_____________________________________________); //填空
printf("|\n");
for(k=(height-1)/2+1; k<height-1; k++){
printf("|");
for(i=0;i<width-2;i++) printf(" ");
printf("|\n");
}
printf("+");
for(i=0;i<width-2;i++) printf("-");
printf("+\n");
```
}
int main()
{
StringInGrid(20,6,"abcd1234");
return 0;
}
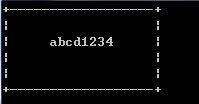
对于题目中数据，应该输出：
+------------------+ | | | abcd1234 | | | | | +------------------+
（如果出现对齐问题，参看【图1.jpg】）
注意：只填写缺少的内容，不要书写任何题面已有代码或说明性文字。
题目分析
对于代码填空题, 我们不需要读完全部代码, 只需要知道需要填空的地方完成的是什么样的功能即可.
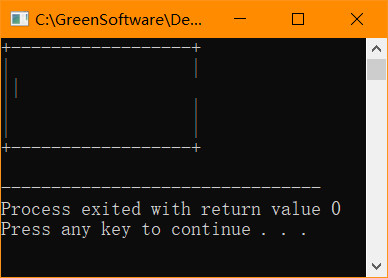
首先, 我们可以先把需要填空的地方注释掉, 看看没有这一句代码的话程序的执行结果是怎样的(如果缺少该句代码之后程序可以执行的话). 在本题中注释掉需要填空的代码之后, 运行结果如图 2 所示:
根据显示的结果可以看出, 缺少的代码就是用来打印格子中的字符串和用于对齐的空格的.
本题考查的是 C++ 中的 printf() 函数的 * , 在 C++ 的官网上可以查找到相关的 API. 在 C++ 官网搜索 printf 即可打开关于 printf() 函数的 API 说明文档 (蓝桥杯比赛的计算机上也提供有 C/C++ 的 API 说明文档), 地址如下:
http://www.cplusplus.com/reference/cstdio/printf/?kw=printf
从官网上我们可以找到这样一个说明, 如图 3:
在其下的示例中我们可以看到对 * 用法的演示 (如图 4):
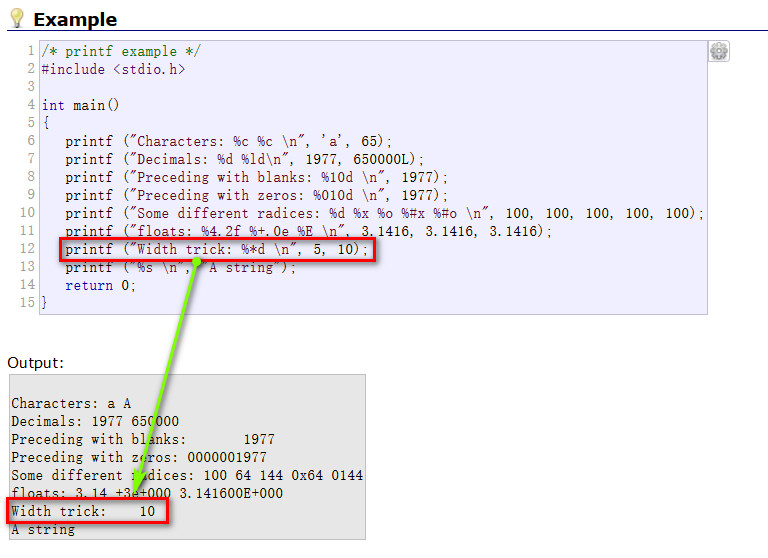
题目中用到的是 %*s , 这里用到的是 %*d, 根据之前学习到的 printf() 函数中 %d 表示整型变量, %s 表示字符型变量的知识可以推测, %*d 和 %*s 也是分别对应整型变量和字符型变量的. 为了验证, 我们可以写这样一段程序:
#include<stdio.h>
int main(){
printf("%*d",3, 9);
printf("\n");
printf("%*s",6, "aa");
return 0;
}
运行结果如下:
9
aa
从输出结果可以发现, 第一行打印出了 2 个空格和 1 个数字 (2+1=3), 第二行打印出了 4 个空格和 2 个字符 (4+2=6).
由此可以看到, printf() 函数中的 * 是用来确定输出的”宽度”的, 需要向其传送两个变量, 一个是宽度值, 一个是要打印的变量, 当要打印的变量的长度小于宽度值时就用空格填充.
再来看需要填空的那行代码:
printf("%*s%s%*s",_____________________________________________);
关键之处是 %*s%s%*s . 根据上面的分析我们知道, 其中间的 %s 是用来打印字符串的, 两边的 %*s 是用来打印空格的. 由于需要对齐, 所以需要知道每行的总长度和字符串的长度才可以计算出要打印的空格的个数.
根据题目中的下面这些代码可以知道每行的长度为 width:
printf("+");
for(i=0;i<width-2;i++) printf("-");
printf("+\n");
由下面这行代码可以确定字符串变量 s 被复制给了变量 buf :
strcpy(buf, s);
strcpy() 函数的功能为:
复制字符串from 中的字符到字符串to，包括空值结束符。返回值为指针to。
来自 C/C++ API 文档
由下面这行代码可以知道字符串变量 s 的长度为 strlen(s) :
if(strlen(s)>width-2) buf[width-2]=0;
由于题目中有如下的说明:
如果不能恰好居中，可以稍稍偏左或者偏上一点。
因此, 当行长度为 20, 字符长度为 8 的时候, 左边的空格应该有 (20-8-2)/2=5 个, 右边的空格应该有 (20-8-2)/2=(20-8-1)/2=5 个. 如果行长度为 21, 字符长度为 8 的时候, 左边的空格应该有 (21-8-2)/2=5 个, 右边的空格应该有 (21-8-1)/2=6 个
由此可以确定, 字符串变量 s 的左边需要打印的空格数为:
(width-strlen(s)-2)/2
右边应该打印的空格数为:
(width-strlen(s)-1)/2
因此空格中应该填写的内容是:
width-2-strlen(s))/2," ",buf,(width-strlen(s)-1)/2," "
完整的程序代码如下:
#include <stdio.h>
#include <string.h>
void StringInGrid(int width, int height, const char* s)
{
int i,k;
char buf[1000];
strcpy(buf, s);
if(strlen(s)>width-2) buf[width-2]=0;
printf("+");
for(i=0;i<width-2;i++) printf("-");
printf("+\n");
for(k=1; k<(height-1)/2;k++){
printf("|");
for(i=0;i<width-2;i++) printf(" ");
printf("|\n");
}
printf("|");
printf("%*s%s%*s",(width-2-strlen(s))/2," ",buf,(width-strlen(s)-1)/2," "); //填空
printf("|\n");
for(k=(height-1)/2+1; k<height-1; k++){
printf("|");
for(i=0;i<width-2;i++) printf(" ");
printf("|\n");
}
printf("+");
for(i=0;i<width-2;i++) printf("-");
printf("+\n");
}
int main()
{
StringInGrid(20,6,"abcd1234");
return 0;
}
2015 年蓝桥杯 C 语言 B 组省赛第 3 题: 三羊献瑞 (三种方法 + 详细分析)
题目
三羊献瑞
观察下面的加法算式：
祥 瑞 生 辉 + 三 羊 献 瑞 ------------------- 三 羊 生 瑞 气
(如果有对齐问题，可以参看【图1.jpg】)
其中，相同的汉字代表相同的数字，不同的汉字代表不同的数字。
请你填写“三羊献瑞”所代表的4位数字（答案唯一），不要填写任何多余内容。
题目分析
将这八个汉字分别用字母 a~h 和数组 aa[0]~aa[7] 对应表示如下:
三 -> a -> aa[0]
羊 -> b -> aa[1]
献 -> c -> aa[2]
瑞 -> d -> aa[3]
祥 -> e -> aa[4]
生 -> f -> aa[5]
辉 -> g -> aa[6]
气 -> h -> aa[7]
换算成题目中的形式分别是:
e d f g
+ a b c d
-------------------
a b f d h
和
aa[4] aa[3] aa[5] aa[6] + aa[0] aa[1] aa[2] aa[3] ------------------------------- aa[0] aa[1] aa[5] aa[3] aa[7]
这里之所以要分别使用字母和数组表示一个汉字是因为下面提到的三种方法要用到.
本题的要求可以总结如下:
- 每个汉字对应的数字都是不同的.
- a~h 这 8 个字母 (或者说 8 个数组元素) 的取值范围是从 0 到 9 十个数字.
- 其中 a (aa[0]) 不能等于 0, e (aa[4]) 也不能等于 0.
- 要求填入的结果是”三羊献瑞”所代表的四位数字, 而不是一共有多少种组合方式 (根据题意可知满足题目条件的组合方式只有一种).
解法一
这个解法基于 C++ 标准函数库 STL 中的 next_permutation() 全排列函数进行. 对 0~9 十个数字进行全排列, 取每次排列的前 8 个代入公式进行计算并检验是否满足要求. 由于进行的是全排列, 所以数组 aa[] 的前 8 个元素都有机会包含 0~9 这 10 个数字.
代码如下:
#include<iostream>
#include<bits/stdc++.h>
using namespace std;
int main(){
int aa[10]={0,1,2,3,4,5,6,7,8,9};
int sum=0;
int sum1=0;
int sum2=0;
int ans=0;
while(next_permutation(aa,aa+10)){
if(aa[0]!=0&&aa[4]!=0){
sum1=aa[4]*1000+aa[3]*100+aa[5]*10+aa[6];
sum2=aa[0]*1000+aa[1]*100+aa[2]*10+aa[3];
sum=aa[0]*10000+aa[1]*1000+aa[5]*100+aa[3]*10+aa[7];
if(sum==(sum1+sum2)){
break;
}
}
}
cout<<"祥瑞生辉:"<<endl;
cout<<" "<<sum1<<endl;
cout<<"三羊献瑞:"<<endl;
cout<<" "<<sum2<<endl;
cout<<"三羊生瑞气:"<<endl;
cout<<sum<<endl;
return 0;
}
正确答案:
1085
解法二
这个解法的思路和解法一类似, 只不过不使用 STL 提供的 next_permutation() 全排列函数, 而改用 8 个 for 循环进行暴力破解.
代码如下:
#include<iostream>
#include<bits/stdc++.h>
using namespace std;
int main(){
int sum, sum1, sum2;
for(int a=1;a<=9;a++){ //a 不能等于 0
for(int b=0;b<=9;b++){
if(b!=a){
for(int c=0;c<=9;c++){
if(c!=a&&c!=b){
for(int d=0;d<=9;d++){
if(d!=a&&d!=b&&d!=c){
for(int e=1;e<=9;e++){ //e 不能等于 0
if(e!=a&&e!=b&&e!=c&&e!=d){
for(int f=0;f<=9;f++){
if(f!=a&&f!=b&&f!=c&&f!=d&&f!=e){
for(int g=0;g<=9;g++){
if(g!=a&&g!=b&&g!=c&&g!=d&&g!=e&&g!=f){
for(int h=0;h<=9;h++){
if(h!=a&&h!=b&&h!=c&&h!=d&&h!=e&&h!=f&&h!=g){
sum1=e*1000+d*100+f*10+g;
sum2=a*1000+b*100+c*10+d;
sum=a*10000+b*1000+f*100+d*10+h;
if(sum==(sum1+sum2)){
printf("%d\n",sum2);
}
}
}
}
}
}
}
}
}
}
}
}
}
}
}
}
return 0;
}
正确答案:
1085
为了进一步验证结果的正确性, 也可以将 8 个汉字对应的结果都输出数来. 由于解法一中已经这么做, 这里就不再加入输出全部计算结果的代码. 输出全部计算结果后需要注意的是, 看清题意和计算结果, 不要误提交不符合题目要求的答案
解法三
这个解法用到了一些数学原理, 可以减少 for 循环的个数, 能够提高计算效率. 虽然对于填空题而言没必要考虑计算效率的问题, 但是这也是一种计算方式, 有必要尝试一下.
首先, 我们看一下这个式子:
e d f g
+ a b c d
-------------------
a b f d h
两个四位数相加得出了一个五位数, 根据加法中”满十进一”的法则, 五位数的最高位一定是 1, 即:
a=1
于是, 原式就变成了:
e d f g
+ 1 b c d
-------------------
1 b f d h
这样我们就可以去掉对 a 的 for 循环, 对解法二中的代码进行一下修改即可.
代码如下:
#include<iostream>
#include<bits/stdc++.h>
using namespace std;
int main(){
int sum, sum1, sum2;
int a=1;
for(int b=0;b<=9;b++){
if(b!=a){
for(int c=0;c<=9;c++){
if(c!=a&&c!=b){
for(int d=0;d<=9;d++){
if(d!=a&&d!=b&&d!=c){
for(int e=1;e<=9;e++){ //e 不能等于 0
if(e!=a&&e!=b&&e!=c&&e!=d){
for(int f=0;f<=9;f++){
if(f!=a&&f!=b&&f!=c&&f!=d&&f!=e){
for(int g=0;g<=9;g++){
if(g!=a&&g!=b&&g!=c&&g!=d&&g!=e&&g!=f){
for(int h=0;h<=9;h++){
if(h!=a&&h!=b&&h!=c&&h!=d&&h!=e&&h!=f&&h!=g){
sum1=e*1000+d*100+f*10+g;
sum2=a*1000+b*100+c*10+d;
sum=a*10000+b*1000+f*100+d*10+h;
if(sum==(sum1+sum2)){
printf("%d\n",sum2);
}
}
}
}
}
}
}
}
}
}
}
}
}
}
}
return 0;
}
一段错误的代码
下面这段代码是错误的:
#include<iostream>
#include<bits/stdc++.h>
using namespace std;
int main(){
int aa[10]={0,1,2,3,4,5,6,7,8,9};
int sum=0;
int sum1=0;
int sum2=0;
int ans=0;
while(next_permutation(aa,aa+10)){
if(aa[0]!=0&&aa[4]!=0){
sum1=aa[4]*1000+aa[3]*100+aa[5]*10+aa[6];
sum2=aa[0]*1000+aa[1]*100+aa[2]*10+aa[3];
sum=aa[0]*10000+aa[1]*1000+aa[5]*100+aa[3]*10;
if(sum==(sum1+sum2)){
break;
}
}
}
cout<<sum1<<endl;
cout<<sum2<<endl;
cout<<sum<<endl;
return 0;
}
运行结果是:
9347 1083 10430
由运行结果可以看到, 最后计算的和为”10430″, 出现了重复的 “0”, 而在题目中的结果里 “三 羊 生 瑞 气” 并没有重复的汉字, 因此这个结果是错误的, 原因在下面这段代码:
sum=aa[0]*10000+aa[1]*1000+aa[5]*100+aa[3]*10;
上面这段代码中没有加入个位, 因此导致错误.
在做题时要注意以下三点:
- 认真读题, 充分理解题意后再做题.
- 认真写代码, 长代码能分行写的就分开写, 不要出现不符合题意的代码.
- 计算出结果后如果能手动验算, 一定要手动验算一遍.
神奇的异或：在不引入第三个变量的情况下交换两个变量的数值
运行环境
操作系统：Windows 7
Python版本：Python 3.7
正文
一般情况下，当我们需要交换两个变量的值的时候，至少需要引入1个第三方变量（当然，如果愿意的话，也可以引入第四方和第五方变量>_<），但是，当我们使用异或的时候就不必这么做，只需要这两个变量就可以完成他们之间数值的交换。
设，有两个变量 a 和 b.
其中，a = 10, b = 20.
现在使用 Python 进行如下的运算：
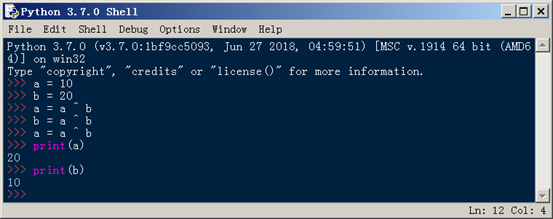
可以看到，经过三次异或操作，成功的交换了a和b的数值。
其实，只要明白了异或的规律，就知道了这其中的原因，异或的运算规则是：
相同为0, 不同为1.
将上面的运算过程展开写就是这样的：
a = a ^ b = 10 ^ 20 = 0b(01010) ^ 0b(10100) = 0b(11110) = 30 b = a ^ b = 30 ^ 20 = 0b(11110) ^ 0b(10100) = 0b(01010) = 10 a = a ^ b = 30 ^ 10 = 0b(11110) ^ 0b(01010) = 0b(10100) = 20